
- •Кафедра физики и высшей математики
- •Часть I
- •Лекция 1. Определители и матрицы
- •1.1. Матрицы: основные сведения
- •1.2. Определители: их вычисление и свойства
- •Определители второго порядка вычисляют по формуле
- •1.3. Действия над матрицами. Обратная матрица. Ранг матрицы
- •1.4. Системы линейных уравнений
- •1.4.1. Метод Крамера
- •1.4.2. Метод обратной матрицы
- •1.4.3. Метод Гаусса
- •Лекция 2. Векторы
- •2.1. Геометрические векторы
- •2.2. Линейные операции над векторами
- •2.3. Проекция вектора на ось
- •2.4. Разложение вектора по осям координат
- •2.5. Линейные операции над векторами, заданными в координатной форме
- •2.6. Скалярное произведение двух векторов
- •2.8. Алгебраический подход к понятию n-мерного вектора
- •2.9. Линейная зависимость векторов
- •Лекция 3. Плоскость и прямая
- •3.1. Плоскость в пространстве
- •3.2. Взаимное расположение двух плоскостей
- •3.3. Прямая в пространстве r3
- •3.4. Две важные задачи аналитической геометрии
- •3.5. Прямая на плоскости
- •Если а 0, в 0, с 0, то прямая (3.11) пересекает обе координатные оси.
- •Раскрывая скобки в уравнении (3.15), получим
- •3.6. Угол между двумя прямыми на плоскости
- •3.7. Площадь треугольника
- •Лекция 4. Введение в анализ
- •4.1. Функция
- •4.2. Предел
- •4.3. Предел переменной величины
- •4.4. Предел функции
- •4.5. Бесконечно малые и их основные свойства
- •4.6. Основные теоремы о действиях с пределами
- •4.7. Сравнение бесконечно малых
- •4.8. Два замечательных предела
- •4.9. Непрерывность функции
- •4.9.1. Приращение аргумента и приращение функции
- •4.9.2. Непрерывность функции в точке
- •4.9.3. Свойств непрерывной на отрезке функции
- •4.10. Некоторые приемы раскрытия неопределенностей вида или при вычислении пределов функции
- •Лекция 5. Дифференциальное исчисление
- •5.1. Производная
- •5.2. Механический смысл производной
- •5.3. Геометрический смысл производной
- •5.4. Дифференцируемость и непрерывность функции
- •5.5. Схема нахождения производной
- •5.6. Таблица производных основных элементарных функций
- •5.7. Правила дифференцирования элементарных функций
- •5.8. Производная сложной функции
- •5.9. Производная параметрически заданной функции
- •5.10. Неявная функция и ее дифференцирование
- •5.11. Дифференциал
- •5.12. Производные и дифференциалы высших порядков
- •5.13. Частные производные
- •5.14. Полный дифференциал
- •Лекция 6. Приложения производной к исследованию функций
- •6.1. Правило Лопиталя
- •6.2. Экстремум функции
- •6.2.1. Возрастание и убывание функции, его аналитические признаки
- •6.2.2. Точка максимума и минимума
- •6.2.3. Необходимое условие экстремума
- •6.2.4. Достаточные признаки существования экстремума
- •6.3. Признаки выпуклости и вогнутости графика функции. Точки перегиба
- •6.3.1. Необходимые и достаточные признаки выпуклости и вогнутости графика
- •6.4. Второй достаточный признак экстремума
- •6.5. Асимптоты
- •6.6. Схема общего исследования функции и построения ее графика
- •Лекции для студентов высших учебных заведений, обучающихся заочно по экономическим специальностям. Часть I
6.3. Признаки выпуклости и вогнутости графика функции. Точки перегиба
График дифференцируемой функции называется выпуклым на интервале, если он расположен ниже любой своей касательной на том интервале; вогнутым (выпуклым вниз), если он расположен выше любой касательной на интервале.
6.3.1. Необходимые и достаточные признаки выпуклости и вогнутости графика
а) Необходимые признаки
Если
график функции у=f(x)
выпуклый
на интервале (a,
b),
то вторая производная
![]() на этом интервале; если график вогнутый
на (a,
b),
то
на этом интервале; если график вогнутый
на (a,
b),
то
![]() на (a,
b).
на (a,
b).
П усть
график функции у=f(x)
выпуклый (a,
b)
(рис.6.3а). Если касательная скользит
вдоль выпуклой кривой слева направо,
то её угол наклона убывает (
усть
график функции у=f(x)
выпуклый (a,
b)
(рис.6.3а). Если касательная скользит
вдоль выпуклой кривой слева направо,
то её угол наклона убывает (![]() ),
вместе с тем убывает и угловой коэффициент
касательной, а значит, убывает первая
производная
на (a,
b).
Но тогда производная первой производной
как производная убывающей функции
должна быть отрицательной, то есть
на (a,
b).
),
вместе с тем убывает и угловой коэффициент
касательной, а значит, убывает первая
производная
на (a,
b).
Но тогда производная первой производной
как производная убывающей функции
должна быть отрицательной, то есть
на (a,
b).
Если
график функции вогнутый
на (a,
b),
то, рассуждая аналогично, видим, что при
скольжении касательной вдоль кривой
(рис. 6.3б) угол наклона касательной
возрастает (![]() ),
возрастает вместе с ним и угловой
коэффициент, а значит и производная. И
тогда производная от производной как
возрастающей функции должна быть
положительной, то есть
на (a,
b).
),
возрастает вместе с ним и угловой
коэффициент, а значит и производная. И
тогда производная от производной как
возрастающей функции должна быть
положительной, то есть
на (a,
b).
б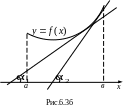 )
Достаточные признаки
)
Достаточные признаки
Если для функции у=f(x) во всех точках некоторого интервала будет , то график функции вогнутый на этом интервале, а если , то выпуклый.
« Правило
дождя»:
Чтобы запомнить какой знак второй
производной связывать с выпуклой, а
какой с вогнутой дугой графика, рекомендуем
запомнить: «плюс вода»
в вогнутой
луночке, «минус вода» - в выпуклой луночке
(рис. 6.4).
Правило
дождя»:
Чтобы запомнить какой знак второй
производной связывать с выпуклой, а
какой с вогнутой дугой графика, рекомендуем
запомнить: «плюс вода»
в вогнутой
луночке, «минус вода» - в выпуклой луночке
(рис. 6.4).
Точка графика непрерывной функции, в которой изменяется выпуклость на вогнутость или наоборот, называется точкой перегиба.
Теорема (достаточный признак существования точки перегиба).
Если
в
точке
![]() функция
дважды дифференцируема и вторая
производная в этой точке равна нулю или
не существует, и если при переходе через
точку
вторая производная
функция
дважды дифференцируема и вторая
производная в этой точке равна нулю или
не существует, и если при переходе через
точку
вторая производная
![]() меняет знак, то точка
есть точка перегиба. Координаты точки
перегиба
меняет знак, то точка
есть точка перегиба. Координаты точки
перегиба
![]() .
.
Точки, в которых вторая производная обращается в нуль или не существует, называются критическими точками второго рода.
Пример
6.4.
Найти точки перегиба и определить
интервалы выпуклости и вогнутости
кривой
![]() (кривая Гаусса).
(кривая Гаусса).
Р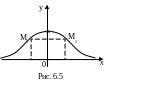 ешение.
Находим первую и вторую производные:
ешение.
Находим первую и вторую производные:
![]() ,
,
![]() .
Вторая производная существует при любых
.
Приравниваем ее нулю и решим полученное
уравнение
.
Вторая производная существует при любых
.
Приравниваем ее нулю и решим полученное
уравнение
![]() ,
где
,
где
![]() ,
тогда
,
тогда
![]() ,
откуда
,
откуда
![]() ,
,
![]() - критические точки второго рода. Проверим
смену знака второй производной при
переходе через критическую точку
.
Если
- критические точки второго рода. Проверим
смену знака второй производной при
переходе через критическую точку
.
Если
![]() ,
например,
,
например,
![]() ,
то
,
то
![]() ,
а если
,
а если
![]() ,
например,
,
например,
![]() ,
то
,
то
![]() ,
то есть, вторая производная меняет знак.
Следовательно,
- абсцисса точки перегиба, ее координаты
,
то есть, вторая производная меняет знак.
Следовательно,
- абсцисса точки перегиба, ее координаты
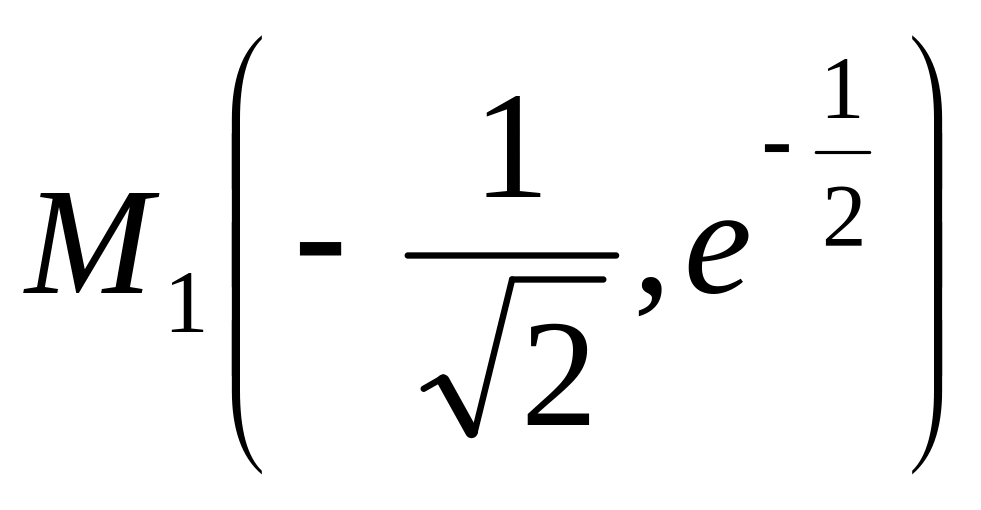 .
Ввиду четности функции
,
точка
.
Ввиду четности функции
,
точка
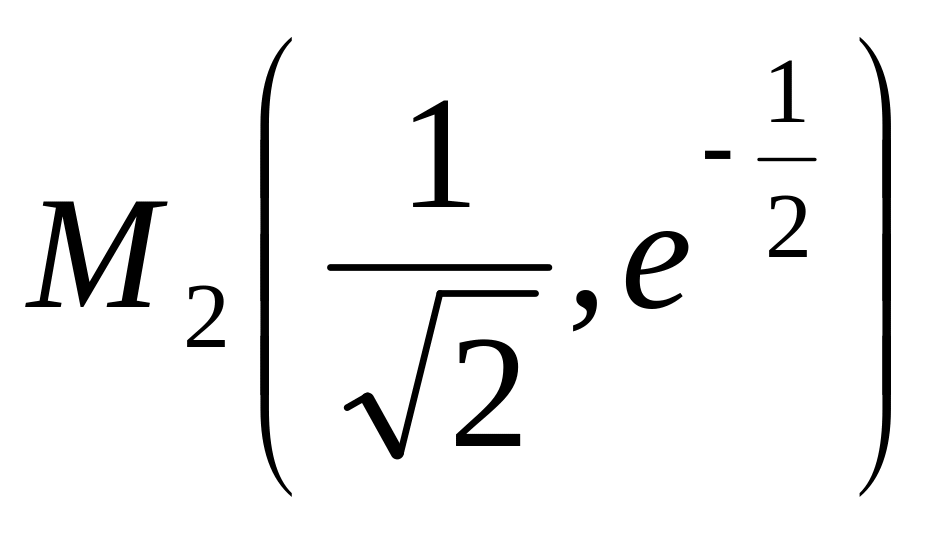 ,
симметричная точке
,
симметричная точке
![]() ,
тоже будет точкой перегиба.
,
тоже будет точкой перегиба.
Итак,
кривая вогнута на интервалах
![]() и
и
![]() кривая выпуклая на интервале
кривая выпуклая на интервале
![]() (рис. 6.5).
(рис. 6.5).
6.4. Второй достаточный признак экстремума
Если
функция
дважды дифференцируема и в некоторой
точке
выполняются условия
,
а
![]() ,
то в этой точке функция имеет экстремум,
причем максимум, если
,
то в этой точке функция имеет экстремум,
причем максимум, если
![]() и минимум, если
и минимум, если
![]() .
.
Пример
6.5.
Найти точку экстремума функции
![]() .
.
Найдем
производные
![]() ;
;
![]() .
Найдем критическую точку первого рода:
.
Найдем критическую точку первого рода:
![]() ,
,
![]() ,
,
![]() - критическая точка. Вычислим
- критическая точка. Вычислим
![]() ,
значит
,
значит
![]() - абсцисса точки минимума. Минимум
функции
- абсцисса точки минимума. Минимум
функции
![]() .
.
Если функция непрерывна в промежутке и имеет единственный экстремум, то он является наименьшим значением функции, если этот экстремум – минимум и наибольшим значением функции, если этот экстремум – максимум.
В прикладных экстремальных задачах нахождение наименьшего или наибольшего значения функции, как правило, сводится к нахождению минимума или максимума функции. В таких задачах больший практический интерес представляют не сами максимумы или минимумы, а те значения аргумента, при которых они достигаются. При решении прикладных задач главная трудность заключается в составлении функции, описывающей рассматриваемый процесс.
Пример 6.6. Дан квадратный лист жести со стороной а. Какого размера квадраты надо вырезать по его углам, чтобы, загнув края, получить коробку наибольшей вместимости.
Р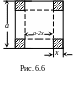 ешение.
Обозначим через
сторону квадрата, который надо вырезать.
Тогда основанием коробки будет квадрат
со стороной
ешение.
Обозначим через
сторону квадрата, который надо вырезать.
Тогда основанием коробки будет квадрат
со стороной
![]() .
Составим функцию объема коробки
.
Составим функцию объема коробки
![]() ,
где
- высота коробки. Или
,
где
- высота коробки. Или
![]() .
Производная этой функции
.
Производная этой функции
![]() .
Найдем критические значения
,
решив уравнение
.
Найдем критические значения
,
решив уравнение
![]() ,
,
![]()
![]() -
не подходит по смыслу задачи;
-
не подходит по смыслу задачи;
![]()
Проверим
характер экстремума при помощи второй
производной. Найдем
![]() .
Подставим
.
Подставим
![]() .
Получим
.
Получим
![]() .
Так как по смыслу задачи
.
Так как по смыслу задачи
![]() ,
то
,
то
![]() .
А если
.
А если
![]() ,
то
- сторона квадрата, при которой объем
будет максимальным. Выше отмечалось,
что если для непрерывной функции
экстремум один и он является максимумом,
то он и есть наибольшее значение функции.
,
то
- сторона квадрата, при которой объем
будет максимальным. Выше отмечалось,
что если для непрерывной функции
экстремум один и он является максимумом,
то он и есть наибольшее значение функции.
