5.11. Дифференциал

Пусть дана дифференцируемая на некотором отрезке [а,Ь] функция . Ее производная, по определению, есть следующий предел

.

А из определения предела следует, что если - предел переменной , то , где  - бесконечно малая, то есть , если . Отсюда получаем приращение функции , состоящее из двух слагаемых. Поскольку в общем случае, а , то первое слагаемое есть главная часть приращения функции при , а второе слагаемое - бесконечно малая величина высшего порядка при , которой во многих задачах можно пренебречь. Главная часть приращения функции называется дифференциалом функции и обозначается символом :

(5.7)

Итак, дифференциал функции есть произведение производной на приращение аргумента.

Рассмотрим функцию и найдем ее дифференциал. По формуле (5.7) получим , откуда видно, что . Тогда формулу (5.7) можно записать так

(5.8)

Из этого соотношения следует, что , то есть, что производная функции есть отношение дифференциала функции к дифференциалу аргумента.

Выше было показано, что , где первое слагаемое есть главная часть приращения. В приближенных вычислениях иногда пользуются равенством , которое в развернутом виде можно записать

откуда (5.9)

Пример 5.7. Вычислить приближенно .

Решение. Будем рассматривать функцию . Найдем ее производную 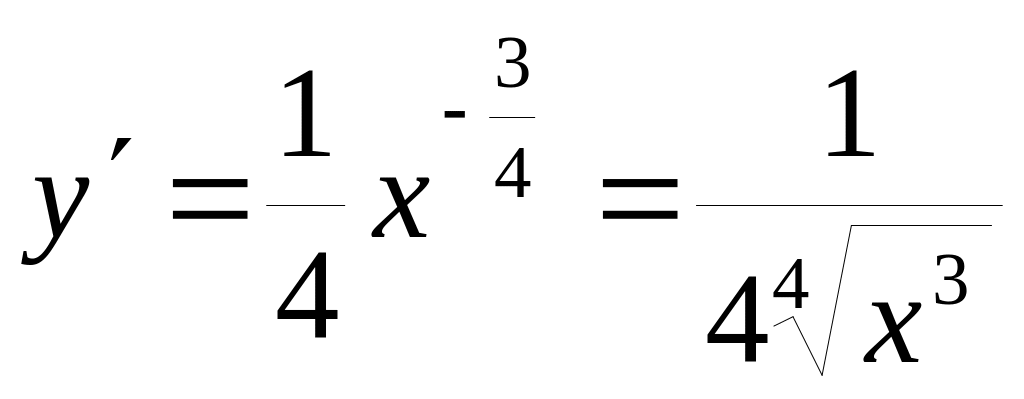. Подставим . Положим в подкоренном выражении (ближайшее целое число, точный корень 4-й степени из которого извлекается и равен 3); . Тогда, по формуле (5.9) будем иметь

.

Поскольку дифференциал функции равен производной этой функции, умноженной на дифференциал независимой переменной, то правила нахождения дифференциала такие же как и для производной. В частности, , , , .

Пример 5.8. Найти дифференциалы следующих функций:

а) ; ;

б) ; ;

в) ; .

5.12. Производные и дифференциалы высших порядков

Пусть функция имеет производную на отрезке . Ее производная тоже будет, вообще говоря, функцией от х. Дифференцируя эту функцию, получим вторую производную или производную второго порядка , а ее производная, то есть - производная третьего порядка и т.д., - производная n-го порядка.

Пример 5.9. Найти производные высших порядков функций:

а) , ;

б) , , , , и т.д.

в) , , , , .

Теперь рассмотрим дифференциалы высших порядков. Если дана функция , имеющая производную, то ее дифференциал по формуле (5.8) будет равен и является тоже функцией от х. Если надо найти дифференциал этой функции, то по той же формуле (5.8) дифференциал 2-го порядка будет таким или . В свою очередь, дифференциал 3-го порядка или и так далее. Вообще дифференциал n-го порядка запишется так

.

Из полученных выражений для дифференциалов 1-го, 2-го, 3-го и т.д. n-го порядков следует такая связь между производными и дифференциалами высших порядков: , , , …, .

Пример 5.10. Дана функция . Найти ее дифференциалы до третьего порядка включительно.

Решение. ,

,

.