
- •Кафедра физики и высшей математики
- •Часть I
- •Лекция 1. Определители и матрицы
- •1.1. Матрицы: основные сведения
- •1.2. Определители: их вычисление и свойства
- •Определители второго порядка вычисляют по формуле
- •1.3. Действия над матрицами. Обратная матрица. Ранг матрицы
- •1.4. Системы линейных уравнений
- •1.4.1. Метод Крамера
- •1.4.2. Метод обратной матрицы
- •1.4.3. Метод Гаусса
- •Лекция 2. Векторы
- •2.1. Геометрические векторы
- •2.2. Линейные операции над векторами
- •2.3. Проекция вектора на ось
- •2.4. Разложение вектора по осям координат
- •2.5. Линейные операции над векторами, заданными в координатной форме
- •2.6. Скалярное произведение двух векторов
- •2.8. Алгебраический подход к понятию n-мерного вектора
- •2.9. Линейная зависимость векторов
- •Лекция 3. Плоскость и прямая
- •3.1. Плоскость в пространстве
- •3.2. Взаимное расположение двух плоскостей
- •3.3. Прямая в пространстве r3
- •3.4. Две важные задачи аналитической геометрии
- •3.5. Прямая на плоскости
- •Если а 0, в 0, с 0, то прямая (3.11) пересекает обе координатные оси.
- •Раскрывая скобки в уравнении (3.15), получим
- •3.6. Угол между двумя прямыми на плоскости
- •3.7. Площадь треугольника
- •Лекция 4. Введение в анализ
- •4.1. Функция
- •4.2. Предел
- •4.3. Предел переменной величины
- •4.4. Предел функции
- •4.5. Бесконечно малые и их основные свойства
- •4.6. Основные теоремы о действиях с пределами
- •4.7. Сравнение бесконечно малых
- •4.8. Два замечательных предела
- •4.9. Непрерывность функции
- •4.9.1. Приращение аргумента и приращение функции
- •4.9.2. Непрерывность функции в точке
- •4.9.3. Свойств непрерывной на отрезке функции
- •4.10. Некоторые приемы раскрытия неопределенностей вида или при вычислении пределов функции
- •Лекция 5. Дифференциальное исчисление
- •5.1. Производная
- •5.2. Механический смысл производной
- •5.3. Геометрический смысл производной
- •5.4. Дифференцируемость и непрерывность функции
- •5.5. Схема нахождения производной
- •5.6. Таблица производных основных элементарных функций
- •5.7. Правила дифференцирования элементарных функций
- •5.8. Производная сложной функции
- •5.9. Производная параметрически заданной функции
- •5.10. Неявная функция и ее дифференцирование
- •5.11. Дифференциал
- •5.12. Производные и дифференциалы высших порядков
- •5.13. Частные производные
- •5.14. Полный дифференциал
- •Лекция 6. Приложения производной к исследованию функций
- •6.1. Правило Лопиталя
- •6.2. Экстремум функции
- •6.2.1. Возрастание и убывание функции, его аналитические признаки
- •6.2.2. Точка максимума и минимума
- •6.2.3. Необходимое условие экстремума
- •6.2.4. Достаточные признаки существования экстремума
- •6.3. Признаки выпуклости и вогнутости графика функции. Точки перегиба
- •6.3.1. Необходимые и достаточные признаки выпуклости и вогнутости графика
- •6.4. Второй достаточный признак экстремума
- •6.5. Асимптоты
- •6.6. Схема общего исследования функции и построения ее графика
- •Лекции для студентов высших учебных заведений, обучающихся заочно по экономическим специальностям. Часть I
5.7. Правила дифференцирования элементарных функций
Из
основных элементарных функций при
помощи арифметических операций сложения,
вычитания, умножения, деления и возведения
в степень можно составить элементарные
функции. Рассмотрим правила их
дифференцирования. Для краткости записей
обозначим одной буквой дифференцируемые
функции
![]() ,
,
![]() ,
,
![]() ,
постоянную величину – буквой С. Итак
имеем правила:
,
постоянную величину – буквой С. Итак
имеем правила:
1)
![]() ,
,
2)
![]() ,
,
3)
![]() ,
,
4)
![]() ,
где
,
где
![]() ,
,
5)
![]() ,
в частности,
,
в частности,
![]() ;
;
![]() .
.
5.8. Производная сложной функции
Пусть
дана сложная функция
такая, что ее можно представить в виде
![]() ,
где
,
где
![]() - промежуточный аргумент. Пусть обе эти
функции дифференцируемы, первая по
- промежуточный аргумент. Пусть обе эти
функции дифференцируемы, первая по
![]() ,
вторая по
,
вторая по
![]() .
.
Рассмотрим
отношение конечных приращений переменных
![]() .
Умножим числитель и знаменатель этой
дроби на конечное приращение
.
Умножим числитель и знаменатель этой
дроби на конечное приращение
![]() .
Получим
.
Получим
![]() .
.
Найдем
пределы выражений в левой и правой
частях этого равенства при
.
Заметим, что функция
![]() ,
дифференцируемы, а значит непрерывны.
Следовательно, при
будет и
,
дифференцируемы, а значит непрерывны.
Следовательно, при
будет и
![]() .
И тогда
.
И тогда
![]()
или
![]() ,
или
,
или
![]() (5.3)
(5.3)
Символ
![]() обозначает
производную функции
по аргументу
обозначает
производную функции
по аргументу ![]() .
.
Правило: Производная сложной функции у по равна произведению производной данной функции у по промежуточному аргументу на производную промежуточного аргумента по конечному аргументу .
Пример
5.2.
Найти
![]() функции
функции
![]() .
.
Решение.
Данную функцию можно представить как
функцию от функции, где
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
По формуле (5.3) получим
.
По формуле (5.3) получим
![]() .
.
Замечание.
Если
![]() ,
где
,
где
![]() ,
,
![]() - два промежуточных аргумента, то
- два промежуточных аргумента, то
![]() ,
и так далее.
,
и так далее.
Пример
5.3.
Найти
функции
![]() .
.
Решение.
Здесь
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
,
![]() .
По формуле (5.4) получим
.
По формуле (5.4) получим
![]() .
Подставляя в правой части вместо
,
.
Подставляя в правой части вместо
,
![]() их значения, выраженные как функции от
,
получим
их значения, выраженные как функции от
,
получим
![]() .
.
5.9. Производная параметрически заданной функции
Функциональная
зависимость ![]() определяет на плоскости
определяет на плоскости ![]() множество точек, координаты которых
связаны этим соотношением. Во многих
случаях эта зависимость весьма сложна
и анализ ее затруднен. В этом случае
бывает целесообразен переход к другим
координатам (например к полярным) или
параметрическое
задание функции.
множество точек, координаты которых
связаны этим соотношением. Во многих
случаях эта зависимость весьма сложна
и анализ ее затруднен. В этом случае
бывает целесообразен переход к другим
координатам (например к полярным) или
параметрическое
задание функции.
В
этом случае координаты точек, связанные
соотношением
задаются как функции параметра
![]() .
.
Например, уравнение Элменса
![]() можно записать в виде
можно записать в виде ![]() ,
,
![]() ,
где
,
где ![]() .
.
Пусть
дана функция
![]() ,
,
![]() ,
где t
– параметр,
,
где t
– параметр,
![]() ,
,
![]() - дифференцируемые функции. Найти
производную
.
- дифференцируемые функции. Найти
производную
.
Рассмотрим
отношение конечных приращений переменных
![]() ,
разделим числитель и знаменатель дроби
на конечное приращение
,
разделим числитель и знаменатель дроби
на конечное приращение
![]() .
.

Ввиду
дифференцируемости функции
,
,
они непрерывны, из чего вытекает, что
при
![]() будет и
будет и
![]() .
Перейдем в предыдущем равенстве к
пределу
.
Перейдем в предыдущем равенстве к
пределу
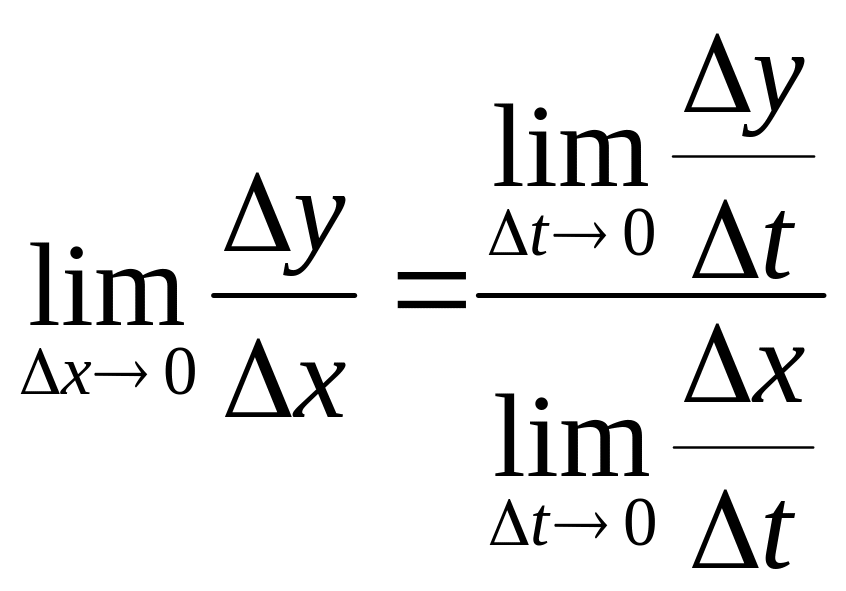
Все эти пределы – производные по определению. Таким образом,
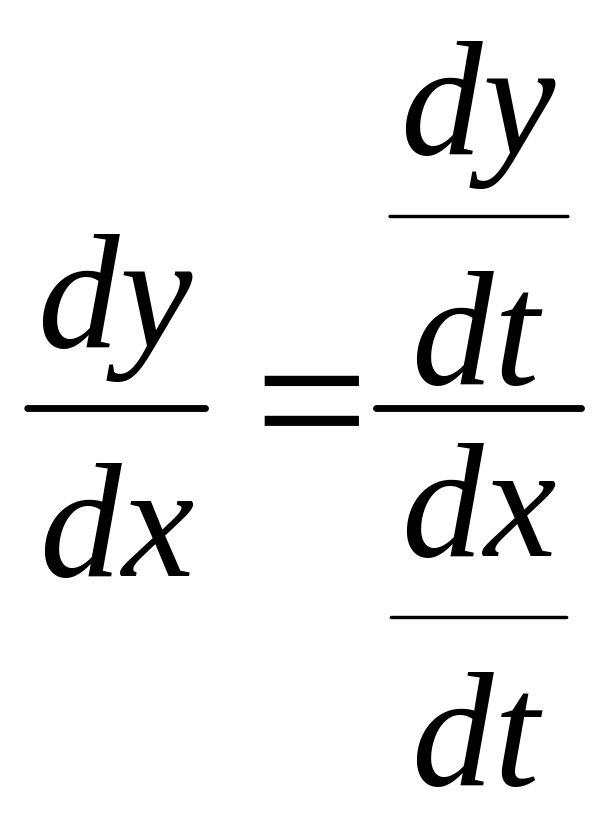 или
или
![]() (5.5)
(5.5)
Пример
5.4.
Дана функция
![]() ,
,
![]() ,
,
![]() .
Найти
.
.
Найти
.
Решение.
Найдем
![]()
![]() .
.
По
формуле (5.5) получим
![]() .
.
5.10. Неявная функция и ее дифференцирование
Если
две переменные
,
связаны между собою функциональной
зависимостью, которую можно записать
в виде
![]() ,
то такую функцию будем называть явной,
то есть такой, из которой явно видно,
что
- независимая переменная, а
- зависимая.
,
то такую функцию будем называть явной,
то есть такой, из которой явно видно,
что
- независимая переменная, а
- зависимая.
Но иногда переменные и связаны зависимостью, символически обозначаемой так:
![]() ,
(5.6)
,
(5.6)
из
которой не видно (не явствует) какая
переменная является независимой, а
какая зависимой. Функции такого вида
называются неявными.
При их дифференцировании одна из
переменных (по вашему выбору, зависящему
от смысла задачи) принимается за аргумент,
а другая за функцию. Так если принять
за аргумент, а
за функцию, то при дифференцировании
по
в тех местах, где встречается
,
следует дифференцировать
как сложную функцию, имея в виду, что
![]() .
.
(Иногда уравнение, задающее неявную функцию, можно разрешить относительно и представить в явном виде).
Пример
5.5.
Найти
![]() функции
функции
![]() .
.
Решение.
Производная суммы равна сумме производных.
Почленно дифференцируя, получим
![]() ,
откуда
,
откуда
![]() .
.
Пример
5.6.
Найти
функции
![]() .
.
Решение.
![]()
![]() ,
(здесь
,
(здесь
![]() )
)
![]()
![]()
![]() .
.
