
- •Кафедра физики и высшей математики
- •Часть I
- •Лекция 1. Определители и матрицы
- •1.1. Матрицы: основные сведения
- •1.2. Определители: их вычисление и свойства
- •Определители второго порядка вычисляют по формуле
- •1.3. Действия над матрицами. Обратная матрица. Ранг матрицы
- •1.4. Системы линейных уравнений
- •1.4.1. Метод Крамера
- •1.4.2. Метод обратной матрицы
- •1.4.3. Метод Гаусса
- •Лекция 2. Векторы
- •2.1. Геометрические векторы
- •2.2. Линейные операции над векторами
- •2.3. Проекция вектора на ось
- •2.4. Разложение вектора по осям координат
- •2.5. Линейные операции над векторами, заданными в координатной форме
- •2.6. Скалярное произведение двух векторов
- •2.8. Алгебраический подход к понятию n-мерного вектора
- •2.9. Линейная зависимость векторов
- •Лекция 3. Плоскость и прямая
- •3.1. Плоскость в пространстве
- •3.2. Взаимное расположение двух плоскостей
- •3.3. Прямая в пространстве r3
- •3.4. Две важные задачи аналитической геометрии
- •3.5. Прямая на плоскости
- •Если а 0, в 0, с 0, то прямая (3.11) пересекает обе координатные оси.
- •Раскрывая скобки в уравнении (3.15), получим
- •3.6. Угол между двумя прямыми на плоскости
- •3.7. Площадь треугольника
- •Лекция 4. Введение в анализ
- •4.1. Функция
- •4.2. Предел
- •4.3. Предел переменной величины
- •4.4. Предел функции
- •4.5. Бесконечно малые и их основные свойства
- •4.6. Основные теоремы о действиях с пределами
- •4.7. Сравнение бесконечно малых
- •4.8. Два замечательных предела
- •4.9. Непрерывность функции
- •4.9.1. Приращение аргумента и приращение функции
- •4.9.2. Непрерывность функции в точке
- •4.9.3. Свойств непрерывной на отрезке функции
- •4.10. Некоторые приемы раскрытия неопределенностей вида или при вычислении пределов функции
- •Лекция 5. Дифференциальное исчисление
- •5.1. Производная
- •5.2. Механический смысл производной
- •5.3. Геометрический смысл производной
- •5.4. Дифференцируемость и непрерывность функции
- •5.5. Схема нахождения производной
- •5.6. Таблица производных основных элементарных функций
- •5.7. Правила дифференцирования элементарных функций
- •5.8. Производная сложной функции
- •5.9. Производная параметрически заданной функции
- •5.10. Неявная функция и ее дифференцирование
- •5.11. Дифференциал
- •5.12. Производные и дифференциалы высших порядков
- •5.13. Частные производные
- •5.14. Полный дифференциал
- •Лекция 6. Приложения производной к исследованию функций
- •6.1. Правило Лопиталя
- •6.2. Экстремум функции
- •6.2.1. Возрастание и убывание функции, его аналитические признаки
- •6.2.2. Точка максимума и минимума
- •6.2.3. Необходимое условие экстремума
- •6.2.4. Достаточные признаки существования экстремума
- •6.3. Признаки выпуклости и вогнутости графика функции. Точки перегиба
- •6.3.1. Необходимые и достаточные признаки выпуклости и вогнутости графика
- •6.4. Второй достаточный признак экстремума
- •6.5. Асимптоты
- •6.6. Схема общего исследования функции и построения ее графика
- •Лекции для студентов высших учебных заведений, обучающихся заочно по экономическим специальностям. Часть I
4.7. Сравнение бесконечно малых
Пусть несколько бесконечно малых , , , … являются функциями одного и того же аргумента x и стремятся к нулю при или . Будем рассматривать их отношения, пользуясь следующими определениями:
1.
Если
![]() ,
то
и
называются бесконечно малыми одного
порядка.
,
то
и
называются бесконечно малыми одного
порядка.
2.
Если
![]() ,
(а
,
(а
![]() ),
то
называется бесконечно малой высшего
порядка
по
сравнению с ,
а
- бесконечно малой низшего
порядка,
по сравнению с .
),
то
называется бесконечно малой высшего
порядка
по
сравнению с ,
а
- бесконечно малой низшего
порядка,
по сравнению с .
3.
Если
![]() ,
то
и
- эквивалентные
бесконечно малые, т.е.:
.
,
то
и
- эквивалентные
бесконечно малые, т.е.:
.
4.8. Два замечательных предела
1)
Предел
функции
![]() при
при
![]() .
.
Ф ункция
ункция
![]() не определена при x
= 0, так как числитель и знаменатель дроби
обращается в нуль. Такое выражение
называют неопределенностью вида
не определена при x
= 0, так как числитель и знаменатель дроби
обращается в нуль. Такое выражение
называют неопределенностью вида
![]() .
Найдем предел этой функции при
.
Рассмотрим окружность радиуса 1 (рис.
4.2). Обозначим центральный угол МОА через
x,
где
.
Найдем предел этой функции при
.
Рассмотрим окружность радиуса 1 (рис.
4.2). Обозначим центральный угол МОА через
x,
где
![]() .
Непосредственно из рисунка 4.2 видно,
что площадь сектора МОА заключена между
площадями треугольников МОА и СОА:
.
Непосредственно из рисунка 4.2 видно,
что площадь сектора МОА заключена между
площадями треугольников МОА и СОА:
пл. МОА < пл. сект. МОА < пл. СОА
или
![]() ,
или после сокращения на
,
или после сокращения на
![]() ,
,
![]() .
.
Разделив
почленно на
![]() ,
получим
,
получим
![]() или
или
![]() .
Переходя к пределу при
и учитывая, что
.
Переходя к пределу при
и учитывая, что
![]() ,
и
,
и
![]() ,
видим, что переменная
заключена между величинами, имеющими
один и тот же предел 1. Тогда, на основании
теоремы 5 о действиях с пределами имеем
,
видим, что переменная
заключена между величинами, имеющими
один и тот же предел 1. Тогда, на основании
теоремы 5 о действиях с пределами имеем
![]() (4.1)
(4.1)
Отсюда следует, что sin x x (sin x эквивалентен х) при .
Число е. Натуральные логарифмы. Экспонента.
Теорема.
Функция
![]() стремится к числу е
при
,
то есть
стремится к числу е
при
,
то есть
![]() ,
(4.2)
,
(4.2)
где число е 2,718281828… Во многих случаях достаточным является приближение е 2,72. Это число прочно вошло в математику и широко используется.
Логарифмы
с основанием е
называют натуральными
логарифмами
и обозначают символом ln.
Если
![]() ,
то
,
то
![]() (4.3)
(4.3)
Связь между десятичными и натуральными логарифмами выражается следующей формулой перехода
![]() (4.4)
(4.4)
где
число
![]() называется модулем
перехода.
называется модулем
перехода.
Еще одним приложением числа е является показательная функция с основанием е – экспонента:
![]() (4.5)
(4.5)
Функции
и
![]() табулированы,
то есть существуют их таблицы.
табулированы,
то есть существуют их таблицы.
4.9. Непрерывность функции
4.9.1. Приращение аргумента и приращение функции
П усть
функция
усть
функция
![]() определена в точке х
= х0
и
некоторой ее
окрестности
с центром в точке х0.
Пусть
определена в точке х
= х0
и
некоторой ее
окрестности
с центром в точке х0.
Пусть
![]() .
Если х
получит
некоторое (положительное или отрицательное)
приращение х
и станет равен
.
Если х
получит
некоторое (положительное или отрицательное)
приращение х
и станет равен
![]() ,
то и функция у
получит
некоторое приращение у.
Новое приращенное значение функции
будет
,
то и функция у
получит
некоторое приращение у.
Новое приращенное значение функции
будет
![]() (рис. 4.5). Итак, разность
(рис. 4.5). Итак, разность
![]() -
приращение
аргумента;
разность
-
приращение
аргумента;
разность
![]() - приращение
функции.
- приращение
функции.
4.9.2. Непрерывность функции в точке
Функция называется непрерывной в точке х0, если она определена в этой точке и некоторой ее окрестности и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то есть
![]() (4.6)
(4.6)
Пример
4.3.
Докажем, что функция
![]() непрерывна в любой точке х0.
Имеем
непрерывна в любой точке х0.
Имеем
![]()
![]() .
Тогда
.
Тогда
![]() .
Пользуясь условием (4.6), найдем предел
.
Пользуясь условием (4.6), найдем предел
![]() .
Это и доказывает непрерывность функции.
.
Это и доказывает непрерывность функции.
Можно
доказать, что всякая
элементарная функция непрерывна в
той
точке, в которой она определена.
Условие непрерывности (4.6) можно записать
и так
![]() ,
где
,
где
![]() -
постоянная
величина,
откуда
-
постоянная
величина,
откуда
![]() .
Приращение
.
Приращение
![]() ,
если
,
если
![]() и
тогда
и
тогда
![]() .
Таким
образом получим
.
Таким
образом получим
![]() .
Но
.
Но
![]() ,
следовательно,
,
следовательно,
![]() .
Иначе говоря, для того, чтобы
найти
предел непрерывной функции при
,
достаточно в выражение функции подставить
.
Иначе говоря, для того, чтобы
найти
предел непрерывной функции при
,
достаточно в выражение функции подставить
![]() ,
что
мы уже делали в примерах 4.1 и 4.2.
,
что
мы уже делали в примерах 4.1 и 4.2.
Пример
4.4.
Функция
![]() непрерывна в любой точке и потому
непрерывна в любой точке и потому
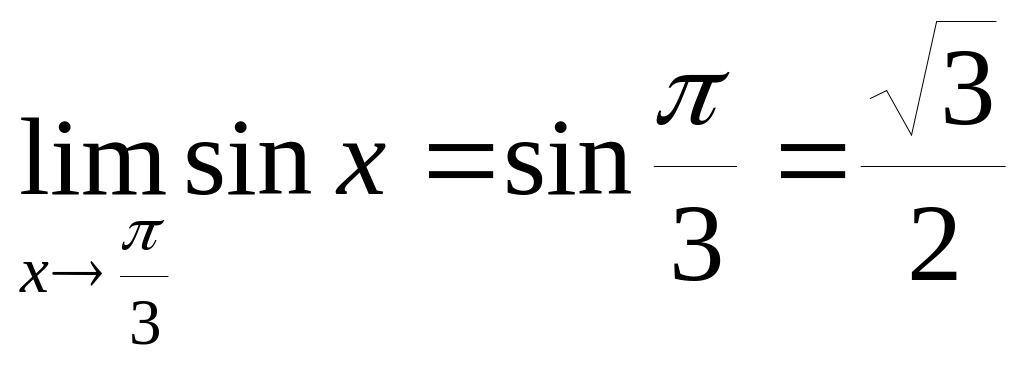 .
.
Если
функция
определена в точке
![]() и ее окрестности и если
и ее окрестности и если
![]() ,
то она непрерывна в точке
.
,
то она непрерывна в точке
.
Если функция непрерывна в каждой точке некоторого интервала (а, b) и непрерывна на концах этого интервала справа и слева, то она называется непрерывной на отрезке [а, b].
Разрывы
функций делят на разрывы первого
и второго ряда.
Если
![]() ,
,
![]() ,
а
,
а
![]() не существует – то
не существует – то ![]() в точке испытывает разрыв
первого рода типа скачок.
в точке испытывает разрыв
первого рода типа скачок.
Пример:
![]() в точке
в точке ![]() .
.
Если
![]() ,а
в -
не существует, то функция
,а
в -
не существует, то функция ![]() в точке испытывает устранимый
разрыв первого рода.
в точке испытывает устранимый
разрыв первого рода.
Пример:
![]() в точке
.
в точке
.
Разрыв, не являющийся не являющийся разрывом первого рода, называют разрывом второго рода.
Примеры:
![]() при
при ![]() , (1)
, (1)
или
![]() при
при
![]() .
(2)
.
(2)
Такие
разрывы как (2) (![]() )
называют бесконечными.
)
называют бесконечными.
