4.4. Предел функции

Рассмотрим некоторые случаи изменения функции при стремлении аргумента х как переменной величины к некоторому пределу а или к бесконечности.

Пусть функция y = f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Функция у = f(х) стремится к пределу при х, стремящемся к , если для каждого сколь угодно малого положительного числа  можно указать такое положительное число , что для всех х, отличных от а и удовлетворяющих неравенству , будет выполняться неравенство .

Е сли b есть предел функции f(x) при , то это обозначают так или при .

Геометрическая иллюстрация последнего определения представлена на рис. 4.1. Видно, что для всех х, отстоящих от а не более, чем на , соответствующая точка М графика функции лежит внутри полосы шириною 2.

Если f(x) стремится к пределу b₁ при х, стремящемся к некоторому числу а так, что х: принимает только значения меньшие а, то пишут , и называют b₁ пределом функции f(x) в точке а слева.

Если х принимает только значения большие, чем а, то пишут и называют b₂ пределом функции f(x)в точке а справа. Это односторонние пределы функции.

Если f(x) стремится к бесконечности при (или ) и при этом принимает только положительные или только отрицательные значения, то пишут или . В этих случаях f(x) называется бесконечно большой величиной. Бесконечно большая величина предела не имеет.

Функция y = f(x) называется ограниченной в данной области изменения аргумента, если существует такое положительное число М, что для всех значений х из данной области выполняется неравенство .

4.5. Бесконечно малые и их основные свойства

Функция а = а(х) называется бесконечно малой при (или ), если ее предел при этих условиях равен нулю. Например, ; .

Сформулируем важные для дальнейшего теоремы о бесконечно малых.

Теорема 1. Если функцию y = f(x) можно представить в виде суммы постоянного числа b и бесконечно малой а, то есть у = b+а, то число b является пределом этой функции: .

Теорема 2. Если , то можно написать у = b+ а, где а – бесконечно малая.

Теорема 3. Если а = а(х) стремится к нулю при (или ), и не обращается в нуль, то обратная ей функция стремится к бесконечности. И обратно, если , то .

Теорема 4. Сумма конечного числа бесконечно малых есть функция бесконечно малая.

Теорема 5. Произведение бесконечно малой функции а = а(х) на функцию ограниченную z = z(x) при есть функция бесконечно малая.

Если ,  - бесконечно малые, то их произведение  тоже бесконечно малая (для любого конечного числа сомножителей).

Если а – бесконечно малая, а , то есть постоянная, то С - бесконечно малая.

4.6. Основные теоремы о действиях с пределами

Будем рассматривать функции u₁, u₂, …, которые зависят от одного и того же аргумента x, при этом аргумент или . Это общее условие позволит нам сократить записи без ущерба для содержания.

Теорема 1. Предел постоянной равен этой же постоянной , где .

Теорема 2. Предел алгебраической суммы конечного числа переменных равен алгебраической сумме пределов этих переменных .

Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же.

Пусть , . Тогда на основании теоремы 1 предыдущего параграфа можем записать

,

где ,  – бесконечно малые, следовательно

.

Так как - постоянная, а - бесконечно малая, то по теореме 2 или .

Следующие теоремы 3 и 4 доказываются аналогично.

Теорема 3. Предел произведения конечного числа переменных равен произведению пределов сомножителей .

Следствие. Постоянный множитель можно выносить за знак предела

Пример 4.1. .

Теорема 4. Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя не равен нулю

Пример 4.2. .

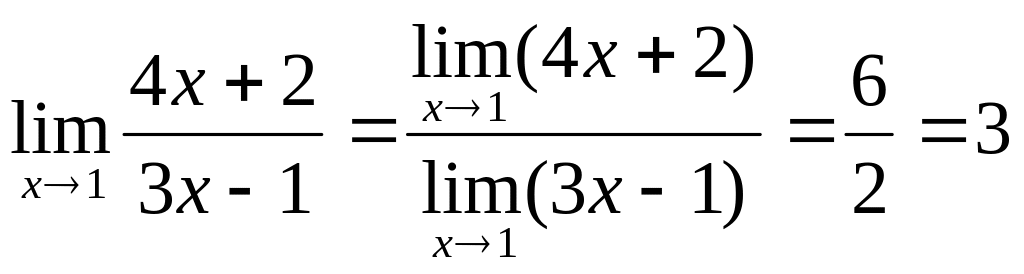Если же предел знаменателя равен нулю или пределы числителя и знаменателя оба равны нулю, то применять теорему 4 нельзя. О том как быть в этих случаях речь пойдет ниже.

Теорема 5. Если - функции, имеющие пределы, причем , и если , то и .

В теории пределов приходится решать две самостоятельные задачи:

1. вычислять предел;

2. доказывать, что предел переменной существует и устанавливать границы, внутри которых предел находится. Иногда эта вторая задача решается с помощью следующей важной теоремы.

Теорема 6. Если переменная величина v возрастающая, то есть каждое ее последующее значение больше предыдущего, и если она ограничена, то есть , то эта переменная величина имеет предел , причем .