
- •030900.62 «Юриспруденция»
- •Программа дисциплины
- •Тема 4. Понятие о математическом моделировании
- •Раздел II. Информатика
- •Тема 1. Информация, информационные процессы. Аппаратные и программные средства реализации информационных процессов. Операционные системы. Офисные приложения
- •Тема 2. Основы и методы защиты информации
- •Тема 3. Алгоритмизация и программирование
- •Тема 4. Локальные и глобальные компьютерные сети
- •Тема 5. Компьютерный практикум по программному обеспечению
- •Методические рекомендации для выполнения контрольных работ
- •Контрольная работа по разделу 1. Математика.
- •Список вопросов для подготовки к экзамену (зачету)
- •Раздел I. Математика
- •Раздел II. Информатика
- •Литература
- •Раздел I. Математика Основная литература:
- •Дополнительная литература:
- •Раздел II. Информатика
- •Глоссарий
- •Раздел I. Математика
- •Раздел II. Информатика
Раздел II. Информатика
Основная литература:
Информатика: базовый курс: учеб. пособие / под ред. С.В. Симоновича. – 2-е изд. – СПб., 2006.
Козырев, А.А. Информатика: конспект лекций / А.А. Козырев, А.П. Юдин. – СПб., 2000.
Дополнительная литература:
Баловсяк, Н.В. Реферат, курсовая, диплом на компьютере / Н.В. Баловсяк. – СПб., 2006.
Вовк, Е.Т. Самоучитель работы на компьютере / Е.Т. Вовк, С.Г. Баричев, О.А. Плотников. – 4-е изд., доп. – М., 2003.
Гиляревский, Р.С. Основы информатики: курс лекций / Р.С. Гиляревский. – М., 2003.
Гукин, Дэн. ПК для «чайников» / Дэн Гукин; пер. с англ. О.В. Зайцевой. – 9-е изд. – М., 2006.
Демина, Л.М. Microsoft PowerPoint в схемах и рисунках: практикум / Л.М. Демина, Р.М. Гатауллин. – М., 2007.
Журин, А.А. Excel 2000: краткие инструкции для новичков / А.А. Журин. – М.; Киров, 2003.
Информатика. Базовый курс: учебник / под ред. С.В. Симоновича. – 2-е изд. – СПб., 2004.
Информатика для юристов и экономистов: учебник для вузов / под ред. С.В. Симоновича. – СПб., 2005.
Каймин, В.А. Информатика: учебник / В.А. Каймин. – 3-е изд. – М., 2003.
Капелюх, С.А. Электронная почта: самоучитель / С.А. Капелюх. – СПб., 2006.
Копыл, В.И. Microsoft Excel / В.И. Копыл. – Минск, 2003.
Кронан, Джон. Microsoft Office Access 2003 / Джон Кронан, Вирджиния Андерсен, Бренда Брайант Андерсон; пер. с англ. О.Б. Вереиной. – М., 2005.
Левин, А.Ш. Windows – это очень просто! / А.Ш. Левин. – СПб., 2005.
Левин, А.Ш. Краткий самоучитель работы на компьютере / А.Ш. Левин. – 2-е изд. – СПб., 2004.
Малюк, А.А. Введение в защиту информации в автоматизированных системах: учеб. пособие / А.А. Малюк, С.В. Пазизин, Н.С. Погожин. – 2-е изд. – М., 2004.
Методическое пособие по курсу пользователь персонального компьютера / сост. А.М. Полонский. – СПб., 2003.
Солоницын, Ю.А. Презентация на компьютере / Ю.А. Солоницын. – СПб., 2006.
Шевченко, Н.А. Access 2003: искусство создания базы данных / Н.А. Шевченко. – М., 2005.
Глоссарий
Раздел I. Математика
Аксиома – предложение, принимаемое без доказательства.
Дискретная случайная величина (ДСВ) – случайная величина, которая может принимать отдельные, изолированные друг от друга значения.
Дисперсия
ДСВ X –
числовая характеристика этой величины,
характеризующая меру рассеивания
значений вокруг математического ожидания
M(X). Дисперсия может быть вычислена двумя
способами:
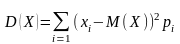 или D(X)=M(X2)-(M(X))2, где xi – значение СВ, pi –
вероятность соответствующего значения
СВ (i= 1, 2,…).
или D(X)=M(X2)-(M(X))2, где xi – значение СВ, pi –
вероятность соответствующего значения
СВ (i= 1, 2,…).
Достоверное событие – событие, которое в результате опыта произойдет при любых обстоятельствах.
Классическая
вероятность события А
есть число
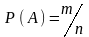 ,
где n – количество всевозможных исходов
опыта, образующих полную группу событий,
m – число исходов опыта, благоприятных
для появления А.
,
где n – количество всевозможных исходов
опыта, образующих полную группу событий,
m – число исходов опыта, благоприятных
для появления А.
Комбинаторное правило суммы: если предмет А можно выбрать n способами, а предмет В – m способами и при этом в k случаях предметы А и В считаются одинаковыми, то хотя бы один предмет, А или В, можно выбрать n+m-k способами.
Комбинаторное правило произведения: если для выбора предмета А существует n вариантов, а для выбора В предмета m вариантов, то упорядоченную пару АВ можно выбрать nm способами.
Математическое ожидание ДСВ X – числовая характеристика этой величины, определяемая следующим образом:
M
(X) =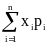 ,
,
где xi – значения СВ, pi – вероятности соответствующих значений СВ .
Невозможное событие – событие, которое в результате опыта не может произойти ни при каких обстоятельствах.
Независимые события – события, появление каждого из которых не влияет на вероятность появления другого.
Несовместные события – события, которые в опыте не могут появляться оба (вместе).
Определение понятия – логическая операция, раскрывающая содержание понятия или устанавливающая значение вводимого термина или символа.
Перестановка
без повторений из n элементов
– любое упорядоченное расположение из
n различных элементов. Число перестановок
без повторений из n элементов вычисляется
по формуле:
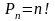 ,
где n! =12…n.
,
где n! =12…n.
Перестановки
с повторениями из k элементов
– упорядоченные выборки из k элементов,
которые не отличаются друг от друга
составом и имеют повторяющиеся элементы,
принадлежащие к одному из m типов. Число
перестановок с повторениями вычисляется
по формуле:
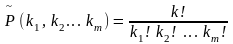 ,
где k1 + k2 + … + km = k и ki + – количество
элементов i- го типа (i =1,2,…, m).
,
где k1 + k2 + … + km = k и ki + – количество
элементов i- го типа (i =1,2,…, m).
Произведением событий А и В называется событие АВ, состоящее в появлении и события А, и события В в результате некоторого опыта.
Размещения
без повторений из n элементов по k
– упорядоченные выборки, которые
получаются при отборе k элементов из n
различных (k
n). Число размещений без повторений из
n элементов по k вычисляется по формуле:
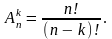
Размещения
с повторениями из n элементов по k
– упорядоченные выборки, которые
составляются из k элементов, каждый из
которых принадлежит одному из n типов
элементов. Число размещений с повторениями
из n элементов по k:
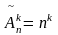 .
.
Ряд распределения ДСВ – это функция, описывающая распределение вероятностей между возможными значениями данной случайной величины. Задается в виде таблицы:
X |
x1 |
x2 |
… |
p |
p1 |
p2 |
… |
где xi – значения СВ, pi – вероятности соответствующих значений СВ .
Случайные величины (СВ) - величины, которые в результате опыта (наблюдения) принимают одно из возможных значений, наперед неизвестное.
Случайные события – любой факт, которые может произойти или не произойти в результате некоторого опыта (действия, наблюднения).
Сочетания
без повторений из n элементов по k
– неупорядоченные выборки, которые
получаются при отборе k элементов из n
различных. Число сочетаний без повторений
из n элементов по k вычисляется по формуле:
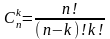 .
.
Сочетания
с повторениями из n элементов по k
– неупорядоченные выборки, которые
получаются при отборе k элементов, каждый
из которых имеет один из n типов. Число
сочетаний с повторениями из n элементов
по k вычисляется по формуле:
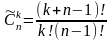 .
.
Суммой событий А и В называется событие А+В, состоящее в появлении в результате некоторого опыта хотя бы одного из событий А или В.
Теорема – предложение, требующее доказательства.
Теорема умножения вероятностей: вероятность произведения событий равна произведению вероятности одного из событий на условную вероятность другого: Р(АВ)= Р(А)РА (В)=Р(В)РВ (А).
Теорема сложения вероятностей: вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А+В)=Р(А)+Р(В)-Р(АВ). Если события А и В несовместны, то Р(А+В)=Р(А)+Р(В).
Формула
полной вероятности:
если событие А может наступить только
при появлении одного из несовместных
событий (гипотез) Н1, Н2… Нn; и
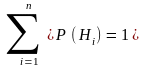 ,
,
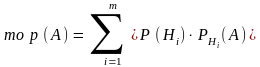 ,
где Р(Нi) – вероятность гипотезы Нi;
,
где Р(Нi) – вероятность гипотезы Нi;
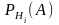 –
условная вероятность события А при
гипотезе Нi.
–
условная вероятность события А при
гипотезе Нi.
Формула
Байеса
применяется для вычисления условной
вероятности гипотезы Нi (i=1,2,…,n) при
условии, что событие А считается
произошедшим:
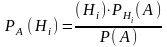 , где Р (А) – вероятность события А, Р
(Нi) – вероятность гипотезы Нi ;
–
условная вероятность события А при
гипотезе Нi.
, где Р (А) – вероятность события А, Р
(Нi) – вероятность гипотезы Нi ;
–
условная вероятность события А при
гипотезе Нi.
Формула
Бернулли:
вероятность того, что в n независимых
испытаниях, в каждом из которых вероятность
события равна p, событие наступит ровно
k раз (безразлично, в какой последовательности),
равна
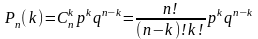 ,
где q=1-p.
,
где q=1-p.
