
Практическое занятие № 9-10 Случайная величина и закон ее распределения
Величина, которая принимает различные числовые значения под влиянием случайных обстоятельств, называется случайной величиной.
Различают дискретные и непрерывные случайные величины.
Случайная величина называется дискретной, если она принимает только определенные отделенные друг от друга значения, которые можно установить и перечислить.
Примеры:
1) число студентов в аудитории – может быть только целым положительным числом: 0,1,2,3,4….. 20…..
2) цифра, которая появляется на верхней грани при бросании игральной кости – может принимать лишь целые значения от 1 до 6.
3) относительная частота попадания в цель при 10 выстрелах - ее значения:
0; 0,1; 0,2; 0,3 ….. 1
Случайная величина называется непрерывной, если она может принимать любые значения внутри некоторого интервала, который иногда имеет резко выраженные границы, а если они не известны, то считают, что значения случайной величины Х лежат в интервале (-; ).. К непрерывным случайным величинам относятся, например, температура, давление, вес и рост людей и т.п.
Понятие случайной величины играет определяющую роль в современной теории вероятностей, разработавшей специальные приемы перехода от случайных событий к случайным величинам.
Закон распределения дискретной случайной величины
Чтобы дать полную характеристику дискретной случайной величины необходимо указать все ее возможные значения и их вероятности.
Соответствие между возможными значениями дискретной случайной величины и их вероятностями называется законом распределения этой величины.
Обозначим
возможные значения случайной величины
Х через
![]() ,
а соответствующие им вероятности через
,
а соответствующие им вероятности через
![]() .
Тогда закон распределения дискретной
случайной величины можно задать тремя
способами: в виде таблицы, графика или
формулы.
.
Тогда закон распределения дискретной
случайной величины можно задать тремя
способами: в виде таблицы, графика или
формулы.
1. В таблице, которая называется рядом распределения, перечисляются все возможные значения дискретной случайной величины Х и соответствующие этим значениям вероятности Р(Х):
-




…
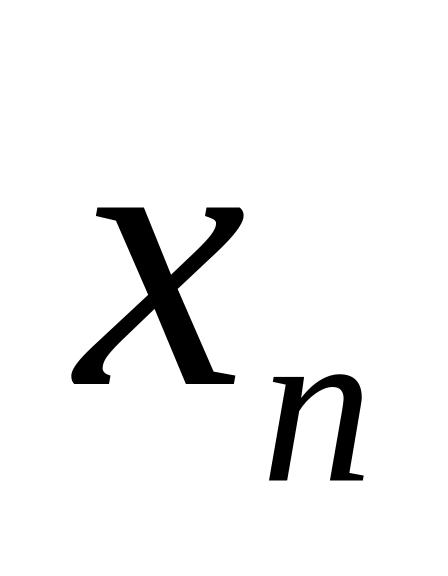
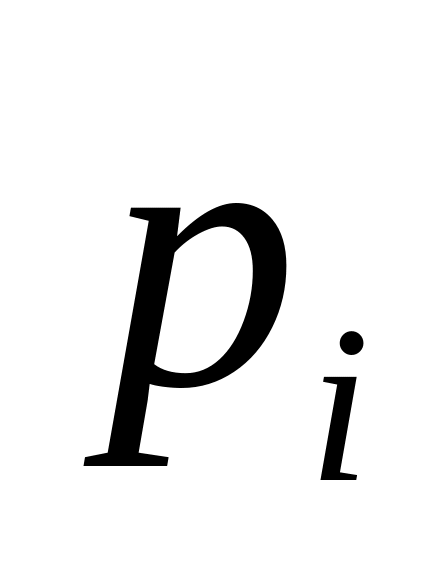
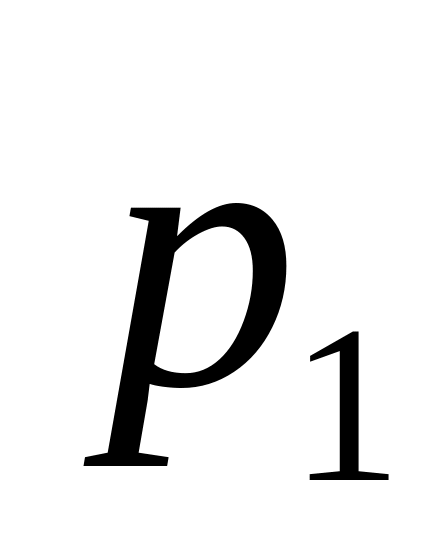
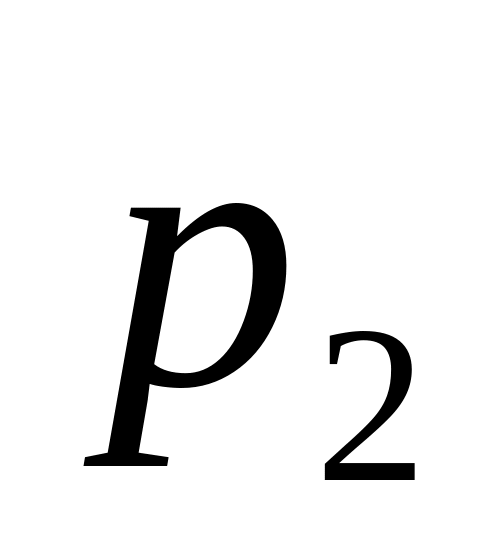
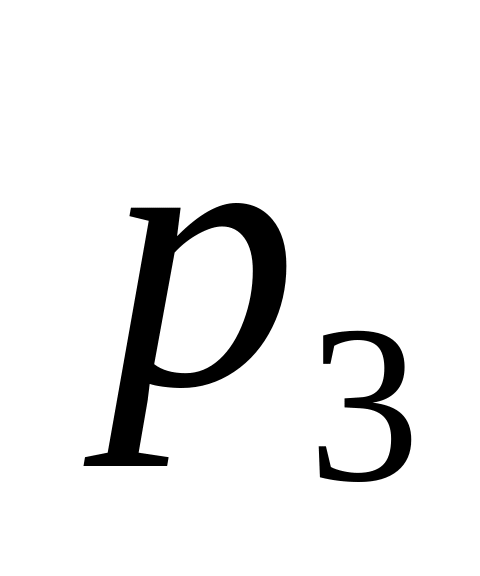
…

П ри
этом сумма всех вероятностей
должна
быть равна единице (условие
нормировки):
ри
этом сумма всех вероятностей
должна
быть равна единице (условие
нормировки):
![]()
2.
Графически
– в виде ломаной линии, которую принято
называть многоугольником
распределения.
Здесь по горизонтальной оси откладывают
все возможные значения
случайной величины
![]() ,
а по вертикальной оси – соответствующие
им вероятности
.
,
а по вертикальной оси – соответствующие
им вероятности
.
3.
Аналитически
- в виде функции:
![]()
Пример 1. В партии из 6 деталей имеется 4 бракованных. Из партии наугад выбирают 2 детали. Составьте закон распределения дискретной случайной величины Х – числа бракованных деталей среди отобранных.
Решение.
В ходе испытания могут получиться следующие комбинации:
1) 0 бракованных и 2 стандартные детали;
2) 1 бракованная и 1 стандартная детали;
3) 2 бракованных и 0 стандартных детали.
Следовательно,
возможные значения Х:
![]()
Найдём соответствующие вероятности возможных значений:
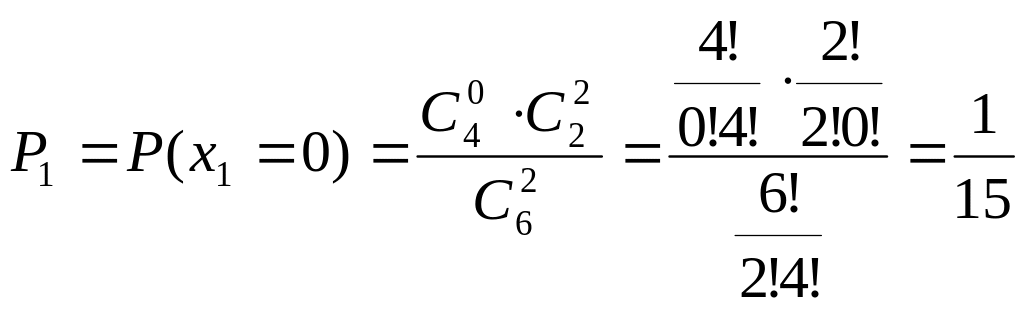 .
.


Следовательно, данная величина Х имеет закон распределения:
Х |
0 |
1 |
2 |
Р |
|
|
|
Проверка:
![]() .
.
