Практическая часть:

1. Рассчитайте профили имплантированных ионов для всех трех случаев – симметричного распределения, слабой асимметрии и сильной асимметрии.

2. В соответствии со своим вариантом выберите энергию ионов (для случая сильной асимметрии) и их тип (для всех трех случаев)

	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5	Вариант 6	Вариант 7	Вариант 8
E, кэВ	10	30	100	10	30	100	30	30
Тип иона	B	B	B	P	P	P	B	P

3. Значение дозы возьмите такое же, что и в предыдущей работе.

Лабораторная работа 3.

Моделирование подвижности электронов в короткоканальных

МОП-транзисторах

Цель работы: Рассчитать распределение значения подвижности электронов по области протекания электрического тока в короткоканальных МОП-транзисторах.

Теоретическая часть:

На рис. 3.1 представлена конструкция моделируемого МОП-транзистора, и в ней в правой части рисунка отмечена область моделирования. Внутри этой области в короткоканальных МОП-транзисторах протекает весь электрический ток, составляющий рабочий ток транзистора – ток стока. В длинноканальных приборах (L_ch>0,7 мкм) это утверждение несправедливо, но они рассматриваться не будут.

Рис. 3.1. Конструкция моделируемого прибора и область моделирования

Величина тока стока внутри области моделирования зависит от концентрации электронов и их подвижности . Оба этих параметра являются сильно неоднородными, т.е. существенно изменяются с координатами x и y, являясь таким образом, функциями и . Точное определение этих функций возможно только с помощью кинетического моделирования электронного переноса в МОП-транзисторе на основе метода Монте-Карло. Однако для подвижности электронов предложено несколько моделей, которые позволяют во многих случаях с высокой степенью точности рассчитать распределение подвижности по области моделирования, т.е. получить функцию .

В модели подвижности в качестве базовых входят четыре параметра — температура кристалла Т, концентрация легируемой примеси в подложке (в нашем случае акцепторной) , напряженности продольной составляющей и поперечной составляющей электрического поля. За исключением температуры три остальных параметра также являются функциями координат, причем зависит только от x (величина концентрации изменяется в глубь подложки, а с изменением y не меняется), зависит только от y (с изменением x не меняется), а зависит и от x и от y.

Рассчитать распределение подвижности можно по следующим трем формулам, которые составляют так называемые модели подвижности Когей–Томаса и Ширахаты:

,

,

.

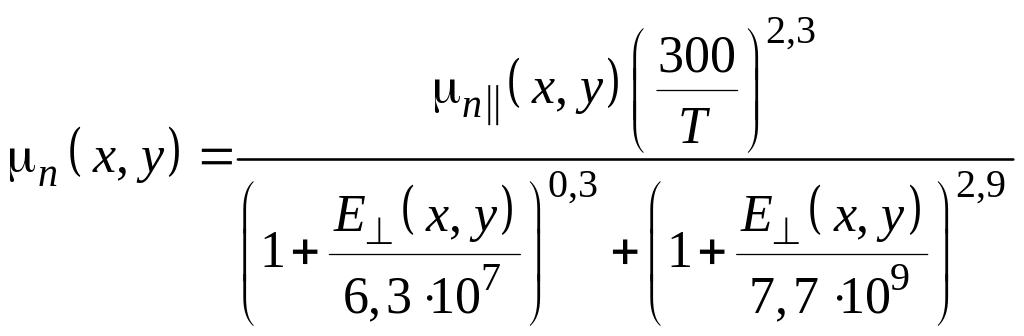Особо следует отметить, что размерности входящих в эти формулы величин следующие: T [К], [м^–3], и [Всм^–1].

Точно определить функции и можно только с помощью численного решения уравнения Пуассона в области моделирования. Однако для многих практических случаев можно воспользоваться аналитическими приближениями. В настоящей работе это будут линейные приближения, т.е. есть линейно возрастающая с ростом функция от 0 до , а есть линейно убывающая с ростом функция от до 0. Причем величина постоянна и равна , а изменяется в области моделирования от 0 у самого истока до у самого стока для любого x. Величина вообще говоря есть функция y, т.е. линейно изменяется вдоль x, но для каждого y будет наблюдаться свое линейное изменение. 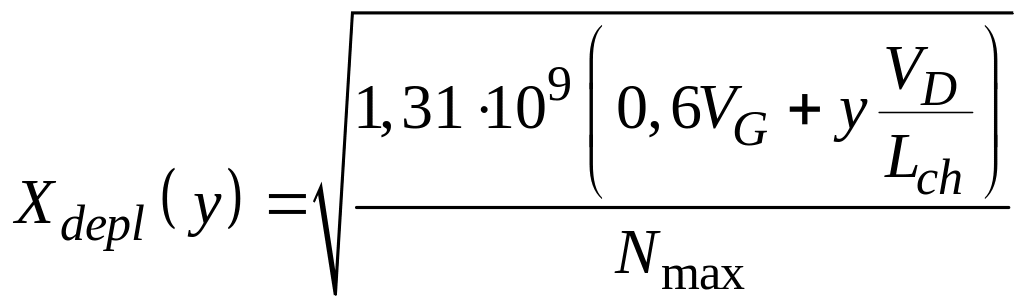Величину можно рассчитать согласно , где и есть максимальное значение концентрации легируемой примеси в подложке. С ростом y, как легко видно из двух последних формул, величина уменьшается (так как растет ).

Замечание: при расчете распределения вдоль любого x нужно иметь в виду, что величина при конкретном значении y равна для и равна 0 для . В то же время область моделирования ограничена размером , величина которого всегда меньше , а для некоторых случаев может наблюдаться и <<

. Это означает, что в действительности в области моделирования величина будет изменяться от до какого-то значения, которое будет заметно больше 0.