Лабораторная работа 1.

Моделирование диффузии примеси в электронных структурах

Цель работы: Рассчитать профили диффундирующих в кремний атомов бора и фосфора.

Теоретическая часть:

Диффузия атомов одного вещества, в частности, бора или фосфора, интенсивно используемых для получения активных областей в приборах интегральной электроники, в объемный образец другого вещества, в частности, кремния, являющегося базовым материалом данной электроники, описывается вторым законом Фика. Его можно записать как

,

где – распределение концентрации диффундирующих в глубь поверхности кремния атомов примеси в определенный момент времени , – коэффициент диффузии соответствующих атомов в кремнии. Точное решение этого уравнения, т.е. нахождение функции возможно, если известны начальное и граничные условия. Начальное условие обычно задается для момента времени в виде – концентрация равна какому-то значению для всех точек в объеме кремния. Чаще всего А = 0. Граничные условия, как правило, задаются для и также в виде установления определенных значений концентрации в этих координатах.

Обычно диффузию атомов примеси в кремнии описывают с помощью двух механизмов – диффузии из бесконечного источника и диффузии из ограниченного источника.

Диффузия из бесконечного источника. Этот механизм задает постоянство концентрации примеси, диффундирующей в глубь кремниевого образца, на его поверхности, а также нулевые значения концентрации в начальный момент времени и на бесконечном удалении от поверхности кремния. Эти условия математически записываются как , , . Используя эти условия, можно получить следующее решение уравнения диффузии, описываемого вторым законом Фика

.

Здесь функция есть дополнительная функция ошибок, которая по определению задается как

.

Значение данной функции можно получить только с помощью численного расчета интеграла. В зависимости от аргумента дополнительная функция ошибок изменяется от 2 для аргументов – 2 и меньше и до 0 для аргументов от 2 и выше.

Диффузия из ограниченного источника. Этот механизм задает постоянство находящегося внутри кремния количества атомов диффузанта, т.е. как бы на поверхность кремния мгновенно произвели осаждение определенного количества атомов примеси и потом эти атомы с течением времени диффундируют в глубь кремния. Физически смысл этого количества атомов в том, что они представляют собой поверхностную концентрацию примеси. Математически начальное и граничные условия записываются как , , . Используя эти условия, можно получить следующее решение уравнения диффузии

.

Учет влияния температуры на диффузию. Физически процесс диффузии представляет собой движение атомов примеси внутри кристалла кремния. Атомы бора и фосфора диффундируют путем занятия вакансий в узлах решетки атомов кремния. Очевидно с изменением температуры процесс диффузии должен каким-то образом менять свой темп, так как атомам диффузанта будет либо легче, либо тяжелее перемещаться по вакансиям. Простой анализ показывает, что с ростом температуры диффузия ускоряется. Это может быть связано с изменением коэффициента диффузии . Был установлен следующий закон зависимости от температуры

,

где – какая-то диффузионная константа, – энергия активация, Кл – заряд электрона, Дж·К^–1 – постоянная Больцмана, – температура. Для атомов бора и фосфора экспериментально были установлены следующие значения диффузионных констант и энергии активации: бор – см²·с^–1, эВ, фосфор – см²·с^–1, эВ.

Ускорение диффузии с ростом концентрации. Однако не только рост температуры ускоряет диффузию – фактически она сама себя ускоряет. Когда в какой-то области кремния концентрация диффундирующей примеси сравняется с собственной концентрацией кремния, сама эта излишняя концентрация примеси становится дополнительным источником диффузии, т.е. диффундирующие в глубь кремния атомы начинают поступать не только от внешнего источника, но и от тех областей внутри кремния, где их становится много – больше собственной концентрации кремния. Это явление можно учесть при определении профиля диффундирующей примеси с помощью следующих моделей коэффициента диффузии.

Для бора при .

Для фосфора при .

Здесь – собственная концентрация кремния, которая является функцией температуры. Но при очень высоких концентрациях примеси – см³ – начинает зависеть и от . Рассчитать величину для конкретных значений температуры и концентрации диффундированной примеси в точке с координатой х можно с помощью следующей модели.

,

,

.

Замечание. В модели собственной концентрации в кремнии размерности всех концентраций [м^–3]. Коэффициент же диффузии дан в размерности [см^3·с^–1] – все расчеты обязательно вести в системе СИ.

Практическая часть:

1. В соответствии со своим вариантом определите какие профили нужно построить. Варианты с 1 по 4 строят профиль бора для механизма диффузии из бесконечного источника и профиль фосфора для механизма диффузии из ограниченного источника. Варианты с 5 по 8 наоборот строят профиль фосфора для механизма диффузии из бесконечного источника и профиль бора для механизма диффузии из ограниченного источника.

2. Нужно построить профили для следующих температур

	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5	Вариант 6	Вариант 7	Вариант 8
Т, К	300 350	250 300	200 300	300 310	300 350	250 300	200 300	300 310

3. Рассчитайте значения D и R для пяти значений энергии в соответствии с нижеприведенной таблицей

	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5	Вариант 6	Вариант 7	Вариант 8
, м–3	2·1024	4·1023	5·1023	2·1023	1024	2·1024	7·1023	8·1023
, м–2	4·1015	5·1015	8·1014	3·1015	9·1014	6·1014	1015	2·1015

4. Постройте зависимости для двух моментов времени с и с. Вы должны построить два графика – отдельно для бора и отдельно для фосфора, и на каждом должны быть по четыре профиля.

Лабораторная работа 2.

Моделирование процесса ионной имплантации при создании легированных карманов в кремнии

Цель работы: Рассчитать распределения концентрации имплантированной примеси в условиях симметричного и асимметричного профилей.

Теоретическая часть:

Процесс ионной имплантации, когда поверхность кремния облучается пучком ионов высокой плотности и разогретых до больших энергий, используется для создания в кремниевом образце областей (так называемых карманов) с высокой концентрацией примеси. Причем пик концентрации не обязательно должен находиться на поверхности кремния. Процесс имплантации задается дозой имплантируемых ионов , которая физически является поверхностной концентрацией ионов в пучке, и энергией ионов Е, величина которой имеет порядок в десятки кэВ.

Проникновение разогретых ионов в глубь кремния и движение в его толще характеризуется тремя параметрами: проецированной длиной пробега , флуктуацией проецированной длины пробега и бокового рассеяния . На рис. 2.1 дано схематичное определение данных параметров.

Рис. 2.1. Определение параметров пробега имплантированных ионов

Экспериментальным путем для ионов бора и фосфора были получены следующие значения этих параметров

Энергия		Е = 10 кэВ	Е = 30 кэВ	Е = 100 кэВ
Бор (B)	, Å	382	1065	3070
	, Å	190	390	690
	, Å	190	465	871
Фосфор (P)	, Å	150	420	1350
	, Å	78	195	535
	, Å	61	168	471

Симметричный профиль. В случае, когда ионы имплантируются с малыми дозами ( < 10¹⁴ м^–2) и энергиями Е (Е < 10 кэВ) в толще кремния формируется профиль примеси практически симметричной формы, который можно описать смещенным распределением Гаусса в виде

.

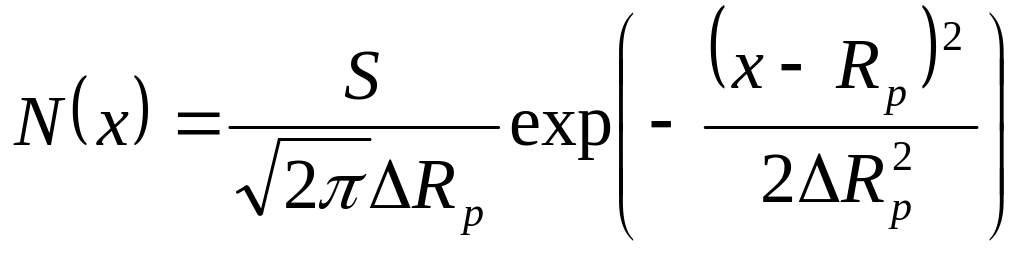Однако обычно расчет осуществляют по чуть более точной формуле

.

Слабая асимметрия профиля. Распределение Гиббонса. С увеличением дозы и энергии профиль имплантированной примеси начинает отличаться от симметричного. Этот случай получил название слабой асимметрии, и профиль описывается распределением Гиббонса, записываемом в следующем виде

,

где , если и , если . Данные параметры называются флуктуацией проецированного пробега и проецированным пробегом в условиях слабой асимметрии. Их значения отличаются от величин и на 10÷20 % в ту или иную сторону. Их точные значения можно найти с помощью следующих трех соотношений

,

Для удобства определения и следует отметить, что первое больше второго приблизительно на величину 0,2 .

Сильная асимметрия профиля. Распределение Пирсона IV типа. При высоких энергиях имплантированных ионов ( кэВ) их профиль в кремнии формируется с довольно существенной асимметрией. Рассчитать данный сильно асимметричный профиль можно только с помощью распределения Пирсона IV типа. Всего математики выделяют 7 разных распределений Пирсона, которые описывают сложные нелинейные распределения случайных величин. Экспериментальные исследования всех получаемых при имплантации ионов профилей показали, что их можно описать с помощью именно распределения Пирсона IV типа. Данное распределение имеет следующий вид

,

,

,

,

,

.

Параметр удовлетворяет следующему соотношению

.

Определить величину можно только рассчитав численно интеграл.

Как видно, все параметры распределения Пирсона IV типа зависят от двух параметров, получивших название асимметрии ( ) и эксцесса ( ). Величины этих параметров в свою очередь зависят от энергии имплантированных ионов. В результате многочисленных экспериментальных измерений были установлены следующие значения асимметрии и эксцесса:

Энергия		Е = 10 кэВ	Е = 30 кэВ	Е = 100 кэВ
Бор (B)		–0,32	–0,85	–1,12
		3,2	4,49	5,49
Фосфор (P)		0,45	0,2	–0,37
		3,4	3,1	3,26

Профиль концентрации примеси, если известен вид распределения Пирсона , легко найти как

.