
- •I. Программа дисциплины «линейная алгебра»
- •1. Линейные пространства
- •2. Системы линейных уравнений. Матрицы и определители
- •3. Многочлены и комплексные числа
- •4. Линейные преобразования и квадратичные формы
- •5. Элементы аналитической геометрии
- •6. Линейное программирование
- •II. Структура зачета и экзамена
- •Методика расчета итоговой оценки
- •III. Содержание зачета и экзамена Теоретические вопросы (а)
- •Теоретические вопросы (б)
- •Практические задания
- •Примеры задач (а)
- •Примеры задач (б)
- •IV. Образцы билетов к зачету (1-ый семестр) Вариант 1
- •Вариант 2
- •Решить матричное уравнение
- •V. Образцы экзаменационных билетов (2-ой семестр) Вариант 1
- •Вариант 2
- •VI. Ответы Примеры задач (а)
- •Примеры задач (б)
- •Образцы билетов для зачета (1-й семестр)
- •Образцы экзаменационных билетов (2-й семестр)
- •VII. Рекомендуемая литература
Примеры задач (б)
1.
![]() ,
,
![]() ;
2.
;
2.
![]() ,
,
![]() ;
3.
;
3.
![]() ,
,
![]() ,
,
![]() ;
4.
;
4.
![]() ;
5.
;
5.
![]() ,
,
![]() ;
6.
;
6.
![]() ;
7.
;
7.
![]() ;
8.
;
8.
![]() ;
9. а)
;
9. а)
![]() ;
б)
;
б)
![]() ;
10. а)
;
10. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
11.
;
11.
![]() ;
12.
;
12.
![]() ,
,
![]() ;
13.
;
13.
![]() ,
,
![]() ;
14.
;
14.
![]() ,
,
![]() ;
15.
,
,
;
15.
,
,
![]() ,
,
![]() ;
16.
;
16.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
17.
;
17.
![]() ;
18.
;
18.
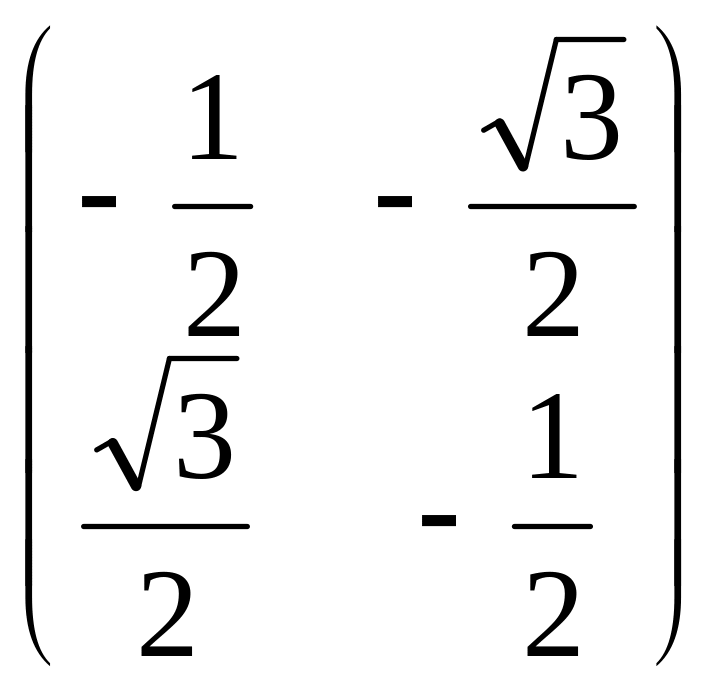 ;
19. а) 8;
б) 72;
в)
;
19. а) 8;
б) 72;
в)![]() ;
20.
;
20.
![]() ;
21. а)
;
21. а)
![]() ;
б)
;
б)
![]() 22. (1; 4); 23.
22. (1; 4); 23.
![]() ;
24.
;
24.
![]() ;
25.
;
25.
![]() ;
26. а)
;
26. а)
![]() ;
б)
;
б)![]() ;
27. а)
;
27. а)
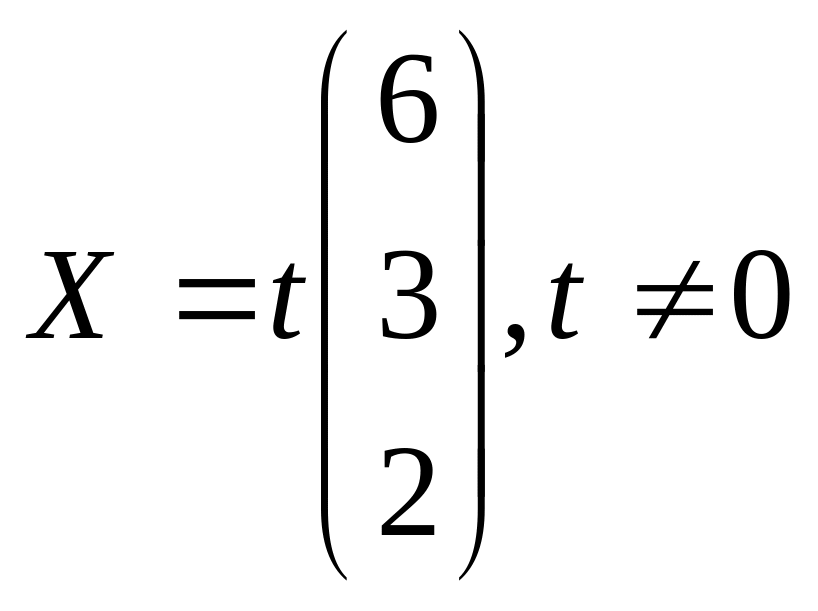 ;
б)
;
б)
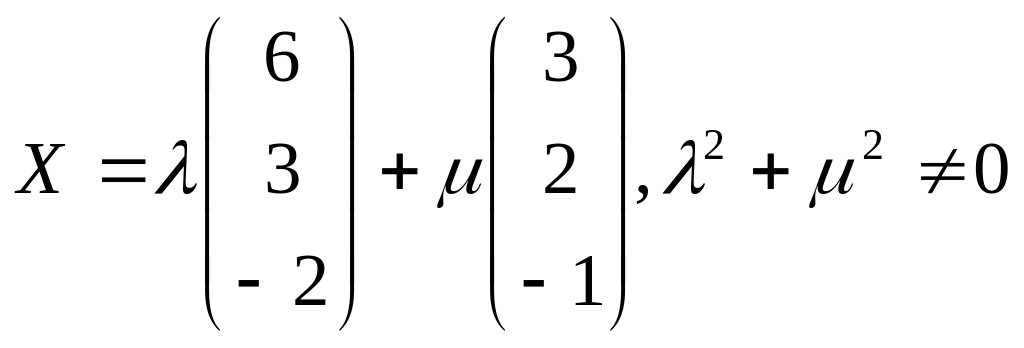 ;
28.
;
28.
![]() ,
;
29. а)
,
;
29. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
30.
;
30.
![]() ;
31.
;
31.
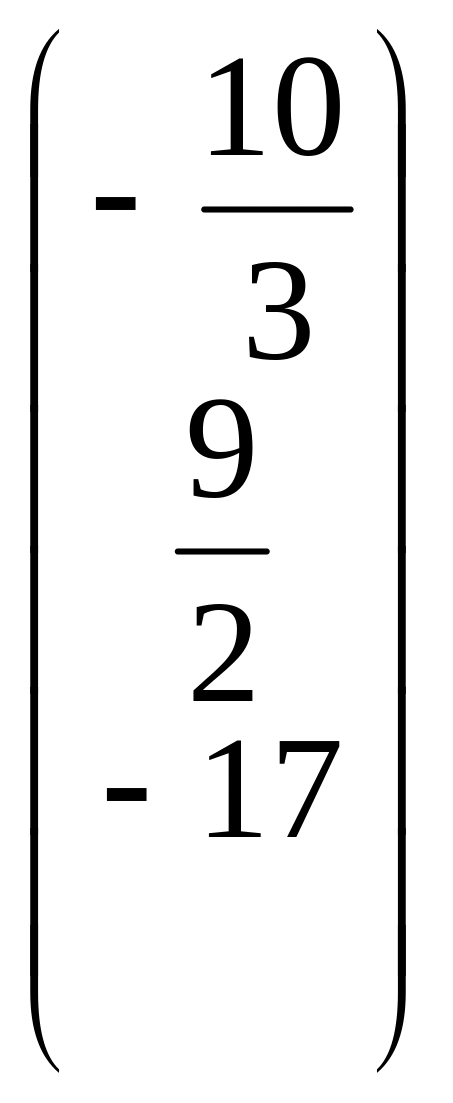 ;
32.
;
32.
![]() ,
,
![]() ,
,
![]() ;
33.
;
33.
![]() ;
34.
;
34.
![]() ;
35.
;
35.
![]() ;
36.
;
36.
![]() ;
37. 12;
38.
;
37. 12;
38.
![]() ;
39.
;
39.
![]() ;
40.
;
40.
![]() ;
41.
;
41.
![]() ;
42.
;
42.
![]() ;
43.
;
43.
![]() ;
44.
;
44.
![]() ;
45.
;
45.
![]() ;
46.
;
46.
![]() ;
47.
;
47.
![]() ;
48.
;
48.
![]() ;
49.
;
49.
![]() ;
50.
;
50.
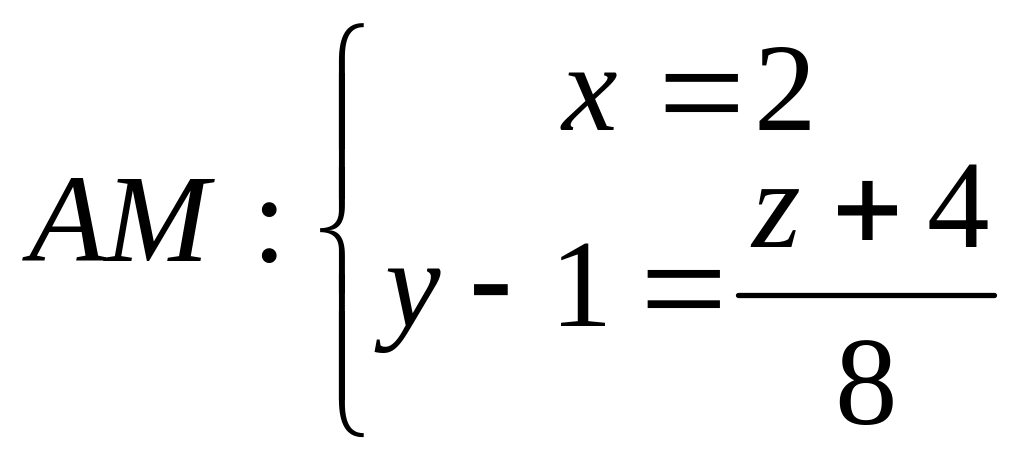 ;
51.
;
51.
![]() ;
52.
;
52.
![]() ;
53.
;
53.
![]() ,
,
![]() ,
,
![]() ;
54.
;
54.
![]() ;
55.
;
55.
![]() ;
56.
;
56.
![]() ;
57. а) (3; 3),
(12; 7), (7; 13); б)
(2;4;0;60;0),
(11;8;60;0;0), (5;12;0;0;60);
58. а) max
в точке
;
57. а) (3; 3),
(12; 7), (7; 13); б)
(2;4;0;60;0),
(11;8;60;0;0), (5;12;0;0;60);
58. а) max
в точке
![]() б) max
в точке
б) max
в точке
![]() min
в точке
min
в точке
![]() 59.
59.
![]()
![]()
![]() .
.
Образцы билетов для зачета (1-й семестр)
Вариант 1
2.![]()
![]()
![]() ;
4.
;
4.
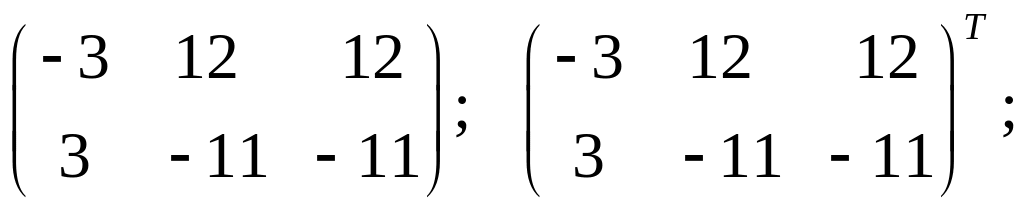
5..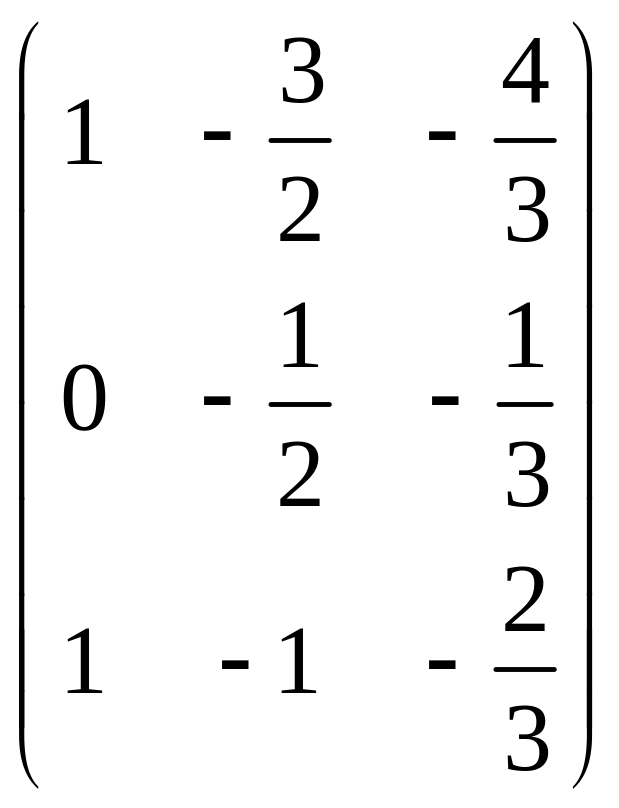 .
.
Вариант 2
3.
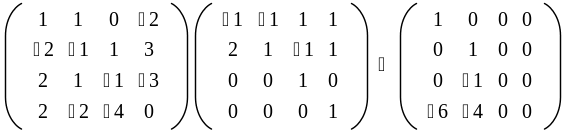 .
.
Ранг матрицы A
равен 2. Ответ.
![]() .4.
114;
.4.
114;
5.
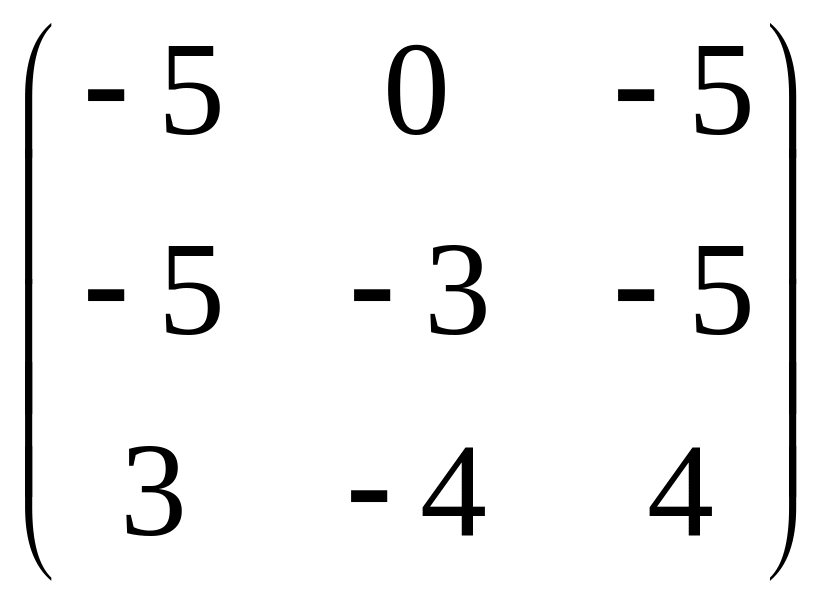 .
.
Образцы экзаменационных билетов (2-й семестр)
Вариант 1
4.
Ответ.
![]() ;
5.
;
5.
 .
6.
48; 7.
.
6.
48; 7.
![]() ,
,
![]() ,
,
![]() ;
8.
Оптимальное решение
;
8.
Оптимальное решение
![]() достигается при
достигается при
![]()
Вариант 2
4.
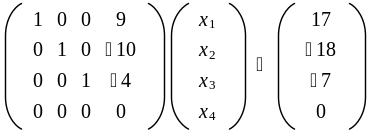 .
Ранг системы равен 3.
.
Ранг системы равен 3.
Частное решение:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
5.
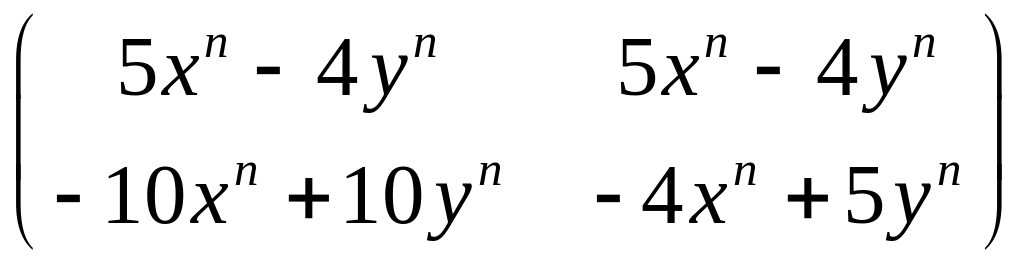 .
.
6. 4.
7.
![]() :
:
![]() ,
,
![]() :
:
![]() ,
,
![]() :
:
![]() .
.
8.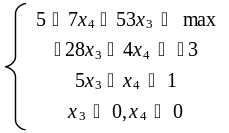 .
.
VII. Рекомендуемая литература
Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике: Учебник для вузов: Ч. 1. – М.: Финансы и статистика, 2003 (рекомендовано Министерством образования РФ).
Калачев Н.В. Линейные и евклидовы пространства. Пособие для бакалавров экономики и менеджмента. Ч. 1, – М.: Финакадемия, 2009. – 130 с. Под редакцией В.Б. Гисина и С.В. Пчелинцева.
Винюков И.А., Попов В.Ю., Пчелинцев С.В. Многочлены и комплексные числа. Собственные значения и собственные векторы. Модель Леонтьева. Пособие для бакалавров экономики и менеджемента. – М.: Финакадемия, 2009.
Тищенко А.В. Линейная алгебра: Элементы аналитической геометрии: Учебное пособие для бакалавриата. Ч. 3. М.: Финакадемия, 2009.
Винюков И.А., Попов В.Ю., Пчелинцев С.В. Линейная алгебра. Ч. 4: Линейное программирование: Учебное пособие для подготовки бакалавров / Под ред. В.Б. Гисина и С.В. Пчелинцева. М.: Финакадемия, 2009.
Бабайцев В.А., Гончаренко В.М., Шандра И.Г. Математика для экономистов. Ч. 1. Линейная алгебра (руководство к решению задач). – М.: Финансовая академия, 2001.
Браилов А.В., Липагина Л.В., Швецов Ю.Н. Математика в экономике. Ч. 2. Аналитическая геометрия. Линейное программирование (руководство к решению задач). – М.: Финансовая академия, 1999.
Браилов А.В., Орлова М.Г., Рылов А.А. Математика для экономистов. Ч. 2. Аналитическая геометрия (руководство к решению задач). – М.: Финансовая академия, 2003.
Волкова Е.С. Теория кривых второго порядка (тексты лекций). – М.: Финансовая академия, 2001.
Пчелинцев С. В. Вопросы и задачи по линейной алгебре. – М.: Финансовая академия, 2006.
Сборник задач по курсу математики (под ред. Солодовникова А.С. и Браилова А.В.). – М.: Финансовая академия, 2001.
Калачев Н.В., Липагина Л.В., Орлова М.Г. Математика. Учебно-методический материал для подготовки домашних контрольных заданий по линейной алгебре с элементами аналитической геометрии и линейному программированию. Часть I. – М.: Финансовая академия, 2005.
Калачев Н.В., Липагина Л.В., Орлова М.Г. Математика. Учебно-методический материал для подготовки домашних контрольных заданий по линейной алгебре с элементами аналитической геометрии и линейному программированию. Часть II. – М.: Финансовая академия, 2005.
Красс М.С. Математика для экономических специальностей. Учебник. – М.: ИНФРА-М, 1999 (рекомендовано Министерством образования РФ).
* Без доказательства (здесь и далее по тексту).
