
Лекция 6
6.1. Прямая линия на плоскости
Из аксиом геометрии известно, что через две точки проходит единственная прямая, и через точку, лежащую на прямой можно провести единственную прямую, перпендикулярную данной прямой.
В плоскости зададим
прямоугольную систему координат и
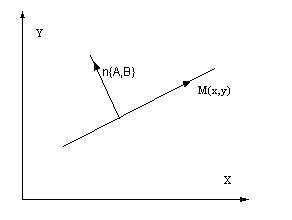
прямую, проходящую через точку
![]() ,
перпендикулярно вектору
,
перпендикулярно вектору
![]() .
Пусть
.
Пусть
![]() -
произвольная точка прямой. Обозначим
через
-
произвольная точка прямой. Обозначим
через
![]() и
и
![]() радиус-векторы точек
и
.
Вектор
радиус-векторы точек
и
.
Вектор
![]() лежит на прямой, а следовательно векторы
лежит на прямой, а следовательно векторы
![]() и
и
![]() перпендикулярны. Значит, их скалярное
произведение равно нулю:
перпендикулярны. Значит, их скалярное
произведение равно нулю:
![]() .
.
Полученное равенство
называется векторным уравнением прямой
на плоскости. Поскольку
![]() ,
то, расписывая это равенство, получаем
следующее уравнение:
,
то, расписывая это равенство, получаем
следующее уравнение:
![]() .
.
Раскрывая скобки
и обозначая:
![]() ,
получим общее
уравнение
прямой:
,
получим общее
уравнение
прямой:
![]() .
.
Вектор
называется
нормальным вектором прямой. Допустим,
что
![]() ,
тогда
,
тогда
![]() .
.
Разделим соотношение на B:
![]() .
.
Обозначим
![]() .
.
Получаем уравнение прямой с угловым коэффициентом:
![]() ,
,
где
![]() – угловой коэффициент прямой,
– угловой коэффициент прямой,
![]() ─
угол, образованный прямой с положительным
направлением оси Ох. Число b
представляет собой величину отрезка,
отсекаемого на оси Оу этой прямой.
─
угол, образованный прямой с положительным
направлением оси Ох. Число b
представляет собой величину отрезка,
отсекаемого на оси Оу этой прямой.
Пусть прямая
проходит через точку
.
Тогда
![]() .
Вычтем полученное соотношение и уравнения
с угловым коэффициентом. Получили
уравнение прямой, проходящей через
точку
,
имеющую угловой коэффициент k:
.
Вычтем полученное соотношение и уравнения
с угловым коэффициентом. Получили
уравнение прямой, проходящей через
точку
,
имеющую угловой коэффициент k:
![]() .
.
Пусть прямая
проходит через точки
![]() и
и
![]() .
Тогда справедливы соотношения
.
Тогда справедливы соотношения
![]() ,
,
![]() .
Разделив одно соотношение на другое
получим уравнение прямой, проходящей
через две
точки:
.
Разделив одно соотношение на другое
получим уравнение прямой, проходящей
через две
точки:
![]() .
.
Определим
направляющий вектор прямой как ненулевой
вектор, параллельный данной прямой.
Найдем уравнение прямой, проходящей
через заданную точку
и имеющей направляющий вектор
![]() .
Очевидно, что точка
лежит на указанной прямой если векторы
.
Очевидно, что точка
лежит на указанной прямой если векторы
![]() и
коллинеарны, а значит, координаты
пропорциональны:
и
коллинеарны, а значит, координаты
пропорциональны:
![]() .
.
Это уравнение и называют каноническим уравнением
прямой линии на плоскости.
Из канонического уравнения можно получить параметрические уравнения прямой. Действительно, из этого уравнения можно записать:
![]() ,
или
,
или
![]()
Эту систему можно
наглядно представить. Если считать t
временем, то координаты х и у есть
координаты точки, двигающейся по линии
с направляющим вектором
и имеющей скорость
![]() .
.
Пусть две прямые
заданы уравнениями с угловыми
коэффициентами:
![]() и
и
![]() ,
причем
,
причем
![]() .
.
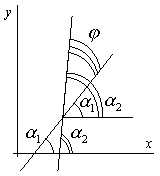
Из геометрических
соображений ясно, что
![]() ,
,
тогда
![]() .
.
Угол между прямыми может быть найден по формуле:
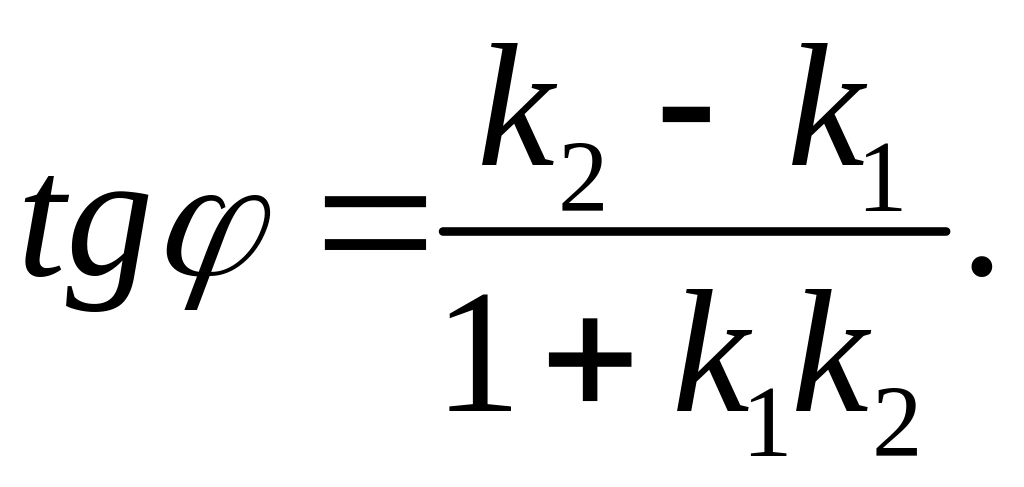
Из данной формулы получаем следующие утверждения.
Условие параллельности
прямых:
![]()
Условие
перпендикулярности прямых:
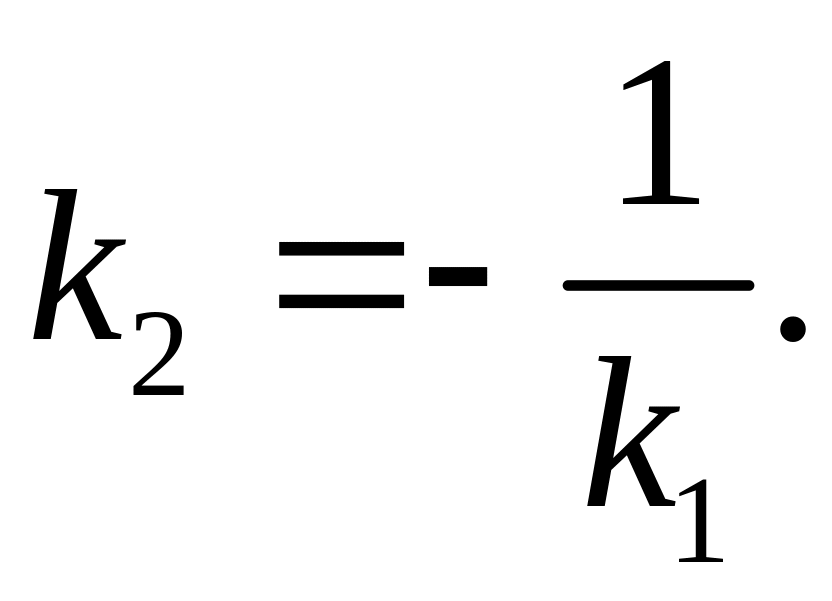
Допустим, что в
общем уравнении
![]() Разделим уравнение
Разделим уравнение
![]() на (- С):
на (- С):
![]() .
.
Обозначив
![]() ,
получим уравнение прямой «в отрезках»:
,
получим уравнение прямой «в отрезках»:
![]() .
.
Эта прямая пересекает оси координат в точках (a, 0) и (0, b).
Уравнение прямой в нормальной форме имеет вид:
![]() ,
,
где р- расстояние
от начала координат до прямой. Общее
уравнение прямой приводится к нормальной
форме умножением на нормирующий множитель
![]() .
Знак выбирается противоположным знаку
свободному члену C,
то есть из условия
.
Знак выбирается противоположным знаку
свободному члену C,
то есть из условия
![]() .
Получается уравнение
.
Получается уравнение
![]() .
.
Расстояние от
точки
![]() до прямой
находится по формуле:
до прямой
находится по формуле:
![]() .
.
Если прямая задана общим уравнением , то расстояние от точки до прямой находится по формуле:
![]() .
.
Пример. Найти уравнения прямых, проходящих через точку М(1,-2) параллельно и перпендикулярно прямой 2х-3у+6=0.
Решение.
Преобразуем уравнение заданной прямой
к виду:
![]() .
Параллельная прямая имеет коэффициент
.
Параллельная прямая имеет коэффициент
![]() ,
ее уравнение
,
ее уравнение
![]() ,
,
![]() .
.
Прямая, проходящая
перпендикулярно, имеет коэффициент
![]() ,
ее уравнение
,
ее уравнение
![]() ,
,
![]() .#
.#
Пример. Даны вершины треугольника A(-2,1), B(3,2), C(1,5). Найти : уравнение стороны АС; длину высоты BD; уравнение медианы АК.
Решение. Для определения уравнения АС используем уравнение прямой, проходящей через две точки:
![]() ,
,
![]() ,
,
![]() .
.
Длину высоты BD найдем как расстояние от точки В(3,2) до прямой АС (4х-3у+11=0):
![]() .
.
Найдем середину
К стороны ВС:
![]() ,
,
![]() .
.
Уравнение медианы АК:
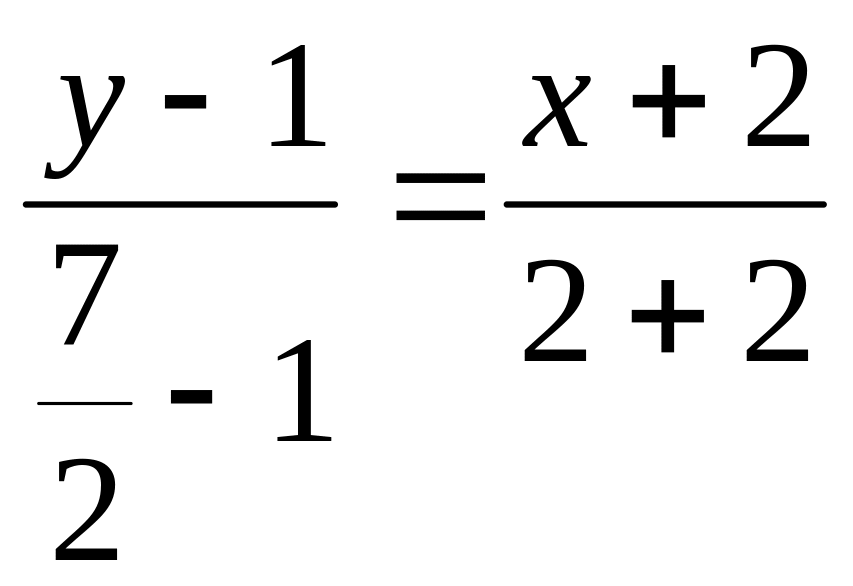 ,
,
![]() ,
,
раскроем скобки и умножим на 2:
![]() .#
.#
