§5. Модель Вселенной с учетом центробежных сил (с-модель)

Как показано в предыдущих параграфах, действие сил отталкивания в однородных идеализированных нерелятивистской и релятивистской Вселенных отличается принципиально. Реальная Вселенная является многокомпонентной. Для правильного описания ее динамики это необходимо учитывать.

Хорошим приближением для описания динамики Вселенной может быть двухкомпонентное приближение, в котором рассматривается идеализированная космическая среда, состоящая из двух однородно перемешанных компонент: нерелятивистской и релятивистской.

Целью настоящего параграфа является подробное описание предлагаемой нами двухкомпонентной космологической модели Вселенной. Существенное отличие этой модели от «стандартной» (ΛCDM- модели) заключается в описании сил отталкивания.

В предлагаемой нами модели, для краткости далее называемой С-модель, учитываем следующее:

космическая среда состоит из двух однородно перемешанных компонент: а) нерелятивистской; б) релятивистской.

В нерелятивистскую компоненту включаются все составляющие космической среды, как наблюдаемые («барионная компонента»), так и ненаблюдаемые (нерелятивистская часть «темной материи»), состоящие из частиц, масса покоя которых много больше их кинетической энергии. Нерелятивистская «темная материя» является кластеризуемой и в настоящее время основной по массе частью всей «темной материи».

Считаем, что влияние давления нерелятивистской компоненты на динамику Вселенной несущественно.

В релятивистскую компоненту включаем все составляющие космической среды, как наблюдаемые (реликтовое излучение), так и ненаблюдаемые (релятивистская часть «темной материи») уравнение состояния для которых . Эта компонента состоит из частиц, масса покоя которых много меньше их полной энергии.

Предположение о присутствии в «темной материи» релятивистской составляющей является важным. Оно позволяет в рамках идеи о центробежной природе космологических сил отталкивания получить достаточную их величину для объяснения наблюдаемой динамики Вселенной. В релятивистскую компоненту включаем все составляющие космической среды, как наблюдаемые (реликтовое излучение), так и ненаблюдаемые (релятивистская часть «темной материи»), уравнение состояния для которой . Эта компонента состоит из частиц масса покоя которых много меньше их полной энергии.

Считаем, что релятивистская составляющая «темной материи» является некластеризуемой. Полагаем, что в настоящее время ее вклад в полную массу «темной материи» не является основным.

Отношение концентраций частиц нерелятивистской компоненты n₁ и релятивистской n₂ в процессе эволюции Вселенной остается постоянным. Учитываем, что, согласно наблюдательным данным n₂ /n₁~10⁹, но, возможно, и значительно больше.

Отметим, что описание некоторых из составляющих «темной материи» (например, нейтрино) должно быть более тщательным и учитывать возможную конечность их массы покоя.

Считаем, что силы отталкивания обусловлены изменением тепловой энергии космической среды.

Исходными при описании динамики Вселенной в рамках С-модели являются космологические уравнения А. А. Фридмана.

Чтобы учесть действие сил отталкивания, производим в этих уравнениях следующие преобразования:

.

(5.1)

Смысл этих преобразований аналогичен тем, которые производились в §3 для идеализированной нерелятивистской Вселенной.

Слагаемые, которые вводятся в космологические уравнения А. А. Фридмана, за счет преобразований (5.1), описывают силы отталкивания, связанные с изменением некоторой энергии, которая взаимосвязана с энергией расширяющейся Вселенной. Это может быть, например, энергия которая связанна с -членом, либо – тепловая энергия космической среды, как мы предполагаем.

Величина определена в расчете на единицу массы космической среды.

С учетом (5.1), обобщенные уравнения А. А. Фридмана для двухкомпонентной среды запишутся в виде:

,	(5.2)
.	(5.3)

Значки 1 и 2, здесь и далее, используются для обозначения нерелятивистской и релятивистской компоненты, соответственно.

При написании уравнений (5.2), (5.3) считаем, что полное давление космической среды . Плотности энергий ₁ и ₂ связаны с плотностями ₁ и ₂ уравнениями: .

Уравнения (5.2), (5.3), легко преобразовать к виду:

,	(5.4)
.	(5.5)

При , уравнение (5.4) описывает не только действие сил гравитации, но и действие сил отталкивания.

Уравнение, описывающее закон сохранения энергии двухкомпонентной космической среды в адиабатическом процессе, имеет вид (5.5) при любом виде функции и значении параметра k.

Уравнение (5.5) в двухкомпонентной модели распадается на два:

,	(5.6)
.	(5.7)

Интегрируя эти уравнения, заключаем, что плотности нерелятивистской ₁ и релятивисткой ₂ компонент связаны с характерным размером Вселенной a(t) соотношениями:

.

(5.8)

Учитывая (5.8), уравнения А. А. Фридмана (5.2), (5.3) запишем в виде:

,	(5.9)
.	(5.10)

Постоянные величины ₁ и ₂ определяются формулами:

, .

(5.11)

Уравнение (5.9) описывает закон сохранения энергии в расчете на единицу массы космической среды. Согласно этому уравнению, сумма кинетической энергии разлета космической среды , энергии , являющейся источником сил отталкивания и потенциальной энергии , являющейся источником сил притяжения, в процессе эволюции Вселенной остается постоянной.

Уравнение (5.10) описывает радиальное движение космической среды в четырехмерном фиктивном пространстве. Первое слагаемое правой части (5.10) описывает действие сил притяжения. Оно связано с изменением потенциальной энергии космической среды. Второе слагаемое описывает силы отталкивания. Они связаны с изменением энергии . Видно, что необходимым условием присутствия объемных сил отталкивания в однородной и изотропной Вселенной является переменность энергии в процессе эволюции Вселенной.

Стандартным уравнениям А. А. Фридмана без учета -члена соответствует . Уравнениям А. А. Фридмана с -членом соответствует «темная энергия»:

,

(5.12)

где  – космологическая постоянная. С учетом (5.12) уравнения А. А. Фридмана (5.2), (5.3) запишутся в виде (2.8), (2.9).

Эти уравнения являются компонентами уравнения Эйнштейна с -членом для однородной и изотропной Вселенной.

Учитывая (2.8) и (2.9) находим радиальное ускорение космической среды обусловленное преобразованием энергии (5.12) в энергию разлета среды:

,

(5.13)

см. (2.13).

Уравнения (2.8), (2.9) лежат в основе «стандартной ΛCDM модели» [6,7]. В рамках идеи о взаимосвязи сил отталкивания с изменением энергии у нас нет разумного объяснения физического смысла формулы (5.12), а, следовательно, и эйнштейновских сил отталкивания.

Считаем правильным другой вариант объяснения сил отталкивания имеющий ясный физический смысл. Полагаем, что энергия (²/2) – это тепловая энергия космической среды в расчете на единицу массы. В предлагаемой С-модели она имеет вид:

,	(5.14)
,	(5.15)

где E(a) и M(a)– тепловая энергия и масса космической среды, соответственно.

Тепловые энергии нерелятивистской E₁ и релятивистской компонент E₂меняются в процессе эволюции Вселенной. Меняется также и отношение E₁/E₂. Есть основание считать, что во все времена, для которых применимо двухкомпонентное приближение, E₂>>E₁. Это обусловлено тем, что число частиц релятивистской компоненты N₂ много больше числа частиц нерелятивистской компоненты (N₂ /N₁~10⁹). В период, когда эти компоненты находились в термодинамическом равновесии . В последующий период отношение E₂ /E₁ растет, так как в это время .

Учитывая эти оценки, вкладом нерелятивистской компоненты в общую тепловую энергию космической среды пренебрегаем и считаем, что E(a)=E₂(a).

Вкладом тепловой энергии E₁ в изменение массы нерелятивистской компоненты также пренебрегаем и считаем, что в процессе эволюции Вселенной масса M₁ этой компоненты остается постоянной.

Масса M₂ излучения в процессе эволюции Вселенной изменяется, но при этом выполняется соотношение:

.

(5.16)

Формулу, определяющую полную массу космической среды , удобно записать в виде:

,

(5.17)

Индексом eq (equality) обозначаем значение величины a в момент, когда во Вселенной достигается равенство плотностей энергий релятивистской и нерелятивистской компонент космической среды. При .

Параметр является одним из определяющих, как в С-, так и в ΛCDM- модели. Учитывая, что , а , заключаем, что величина параметра связана с современными значениями плотностей и формулой:

.

(5.18)

С учетом приведенных выше оценок, тепловую энергию космической среды описываем формулой:

.

(5.19)

Используя (5.17), (5.19), находим удельную тепловую энергию космической среды :

.

(5.20)

Силы отталкивания связаны с изменением тепловой энергии среды в процессе эволюции Вселенной. Величина этих сил, в расчете на единицу массы, определяется формулой:

.

(5.21)

В эпоху преобладания релятивистской компоненты, когда , и :

.

(5.22)

Видно, что в эту эпоху объемные силы отталкивания, в расчете на единицу массы, оставались постоянными.

В эпоху преобладания вещества, когда и , силы отталкивания определяются формулой:

.

(5.23)

Видно, что эти силы аналогичны ньютоновским силам притяжения, но имеют другой знак.
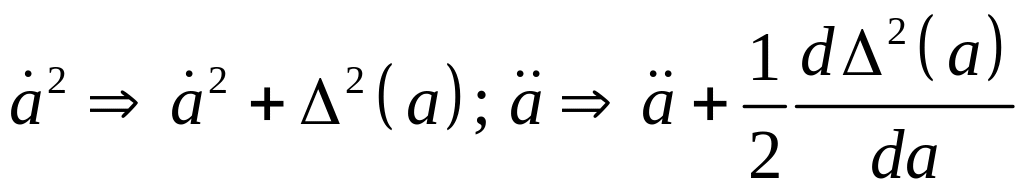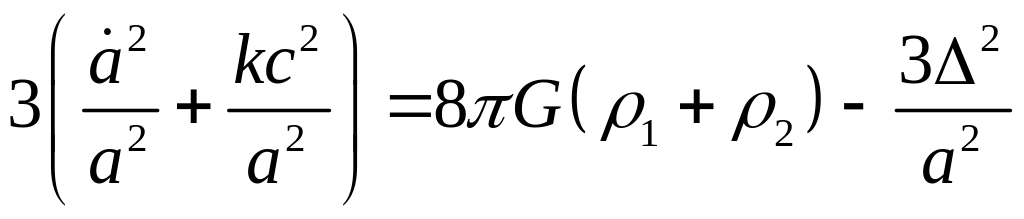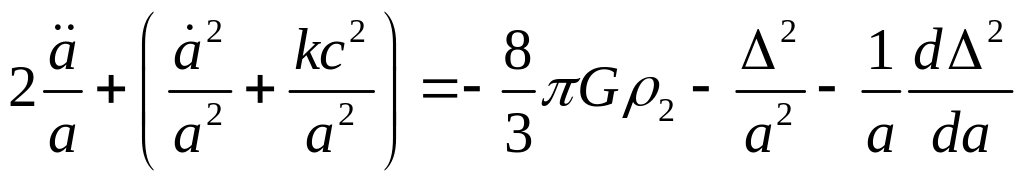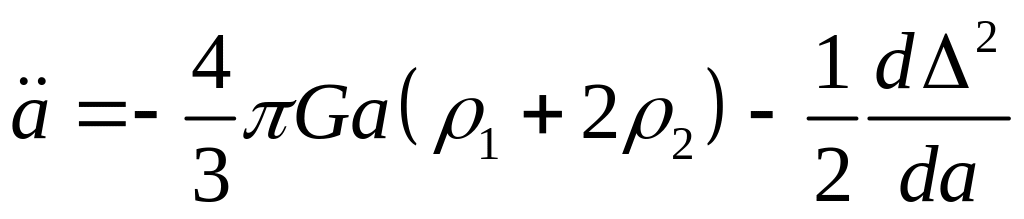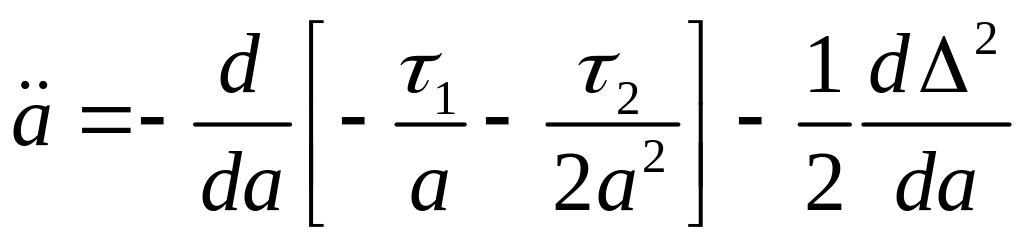