§4 Динамика идеализированной релятивистской Вселенной
В настоящем параграфе рассмотрим следующую задачу. Безграничное однородное и изотропное пространство однородно заполнено чернотельным излучением, уравнение состояния которого имеет вид:
|
(4.1) |
.Значок , здесь и далее, означает, что соответствующая величина описывает излучение.
Изучим динамику этой идеализированной релятивистской Вселенной, для того, чтобы понять, как в этом случае проявляется действие космологических сил отталкивания, связанных с тепловой энергией.
Проведем исследование, используя стандартные космологические уравнения А. А. Фридмана (2.2) и (2.3). С учетом (4.1), эти уравнения запишем в виде:
|
(4.2) |
|
(4.3) |
,
.
Преобразования вида
,
которые могли бы иметь смысл учета
энергии излучения, структуры уравнений
А. А. Фридмана не меняют, поэтому можно
думать, что энергия излучения в уравнениях
(4.2), (4.3) уже учтена.
Уравнения (4.2), (4.3) можно преобразовать к виду:
|
(4.4) |
|
(4.5) |
.
.Эти уравнения имеют место при любом значении постоянной k.
Интегрируя уравнение (4.5), получаем:
|
(4.6) |
.Учитывая термодинамические свойства чернотельного излучения, заключаем, что с изменением масштаба Вселенной a, частота излучения , температура T и плотность частиц n меняются следующим образом:
|
(4.7) |
.Уравнение (4.4), с учетом (4.6), запишем в виде:
|
(4.8) |
Величина , определяется формулой:
|
(4.9) |
.В процессе эволюции Вселенной эта величина остается постоянной.
Первым интегралом уравнения (4.8) является энергия
|
(4.10) |
.Уравнение (4.10) с учетом (4.9) можно записать в виде:
|
(4.11) |
.Сравнивая (4.2) и (4.11), заключаем, что параметр k, определяющий тип кривизны пространства, связан с энергией E формулой:
|
(4.12) |
.Конкретным начальным условиям соответствует определенное значение энергии E, а, следовательно, и параметра k. В зависимости от того, E < 0, E = 0 или E > 0, принципиально различными являются решения, описывающие динамику релятивистской Вселенной, различными являются и типы пространств, соответствующие этим решениям.
Из уравнения (4.8) видно, что динамику релятивистской Вселенной определяют только силы притяжения.
Этот результат может вызвать сомнение. Возникает вопрос: почему в идеализированной нерелятивистской однородной Вселенной силы отталкивания действуют, а в идеализированной Вселенной, заполненной излучением, таковые отсутствуют? Поясним с чем это связано.
В идеализированной нерелятивистской Вселенной удельная тепловая энергия в расчете на единицу массы изменяется в процессе эволюции Вселенной. Это влияет на радиальное движение космической среды. Ускорение, обусловленное силами отталкивания, определяется формулой (3.32).
Совершенно другая ситуация в идеализированной Вселенной, однородно заполненной излучением. Удельная тепловая энергия в этом случае определяется формулой:
|
(4.13) |
.В процессе эволюции Вселенной эта энергия не меняется. Вследствие этого динамика релятивисткой Вселенной определяется лишь изменением потенциальной энергии излучения в гравитационном поле.
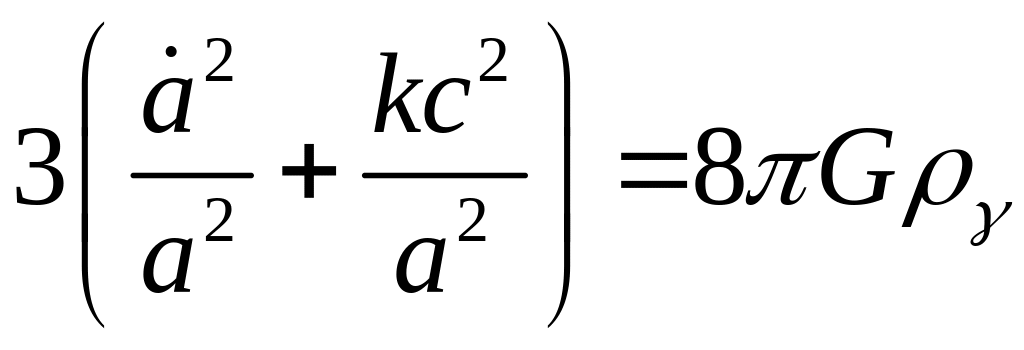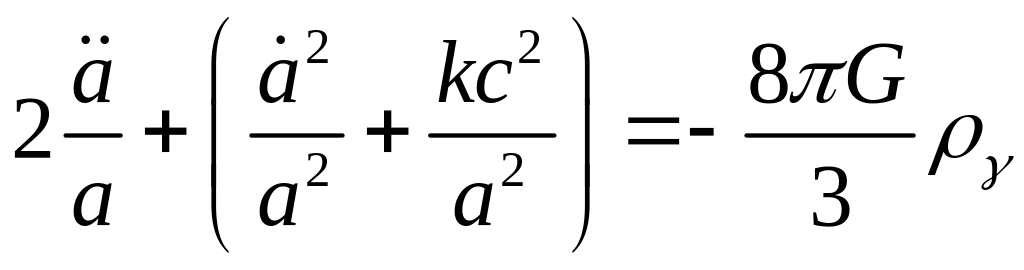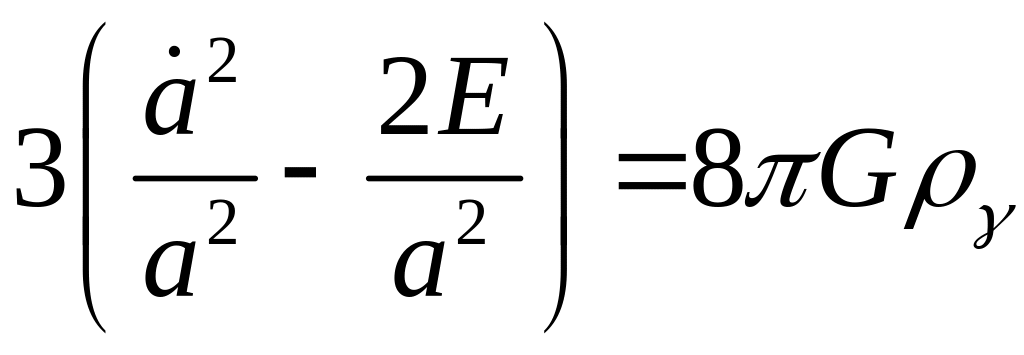