Динамика d–мира в сопутствующей системе координат

Находясь в сопутствующей системе координат , не выходя из D–мира и учитывая лишь локальные его свойства, описать динамику D–мира сложно. В то же время, зная уравнения, описывающие его динамику в сферических координатах, переписать их на случай двухмерной криволинейной, внутренней для D–мира полярной системы координат не составляет труда.

В процессе эволюции D–мира, расстояние между D–наблюдателями меняется. Если – расстояние между двумя произвольными D–наблюдателями в сопутствующей системе координат в момент времени , а это же расстояние, но в начальный момент времени, то очевидно, что для любых пар D–наблюдателей справедливо равенство:

.

(П.61)

Индекс 2 здесь и далее обозначает размерность D–мира. Используя обозначение: и учитывая (П.52) и (П.61) заключаем, что уравнение для будет иметь вид:

,

(П.62)

где

.

(П.63)

Решения уравнения (П.62) должны удовлетворять начальным условиям:

.

(П.64)

Уравнения (П.62), (П.64) совершенно аналогичны уравнениям (П.52) и (П.53).

Учитывая (П.47) и (П.48) находим, как меняются в сопутствующей системе координат концентрация частиц и кинетическая энергия в расчете на единицу массы:

,	(П.65)
.	(П.66)

Отметим некоторые особенности рассмотрения D–мира с точки зрения произвольного D–наблюдателя. Изучая свой мир, он отметит следующее:

-мир является двухмерным, однородным, изотропным и нестационарным;

-радиус кривизны одинаков во всех точках D–мира;

-движение других типичных наблюдателей, относительно него подчиняется закону Хаббла: не зависит от , а есть функция лишь времени ( );

-через точку, в которой он находится все частицы движутся с одинаковой скоростью ; распределение скоростей по направлениям является изотропным;

-изменение концентрации частиц n(t) и дисперсии скоростей однозначно связано с изменением и описывается формулами (П.65), (П.66).

Спросим себя, может ли D–наблюдатель, основываясь лишь на своем локальном опыте, написать уравнения описывающие динамику его мира (П.62) – (П.66)? Сможет ли он понять, почему микроскопические скорости движения частиц ответственны за возникновение сил отталкивания?

Для правильного решения задачи ему необходимо понять следующее:

-геометрия его мира не является евклидовой, а центр его мира не является точкой его пространства;

-для описания динамики D-мира удобно использовать фиктивное для него трехмерное пространство. Разумеется, оно не имеет ничего общего с трехмерным пространством-временем D-мира. Отметим, что использование фиктивного евклидового пространства большей размерности удобно для описания геометрических свойств не только искривленного пространства D-мира, но и пространства однородной изотропной Вселенной (см., например, §107 [22]);

-его пространство является двухмерной однородной, изотропной поверхностью в этом фиктивном пространстве. Радиус кривизны поверхности меняется со временем.

-изменение радиуса кривизны определяется действием гравитационных и центробежных сил, действующих в фиктивном для него третьем измерении. Эти силы в его мире проявляются как силы притяжения и силы отталкивания;

-для любых пар типичных наблюдателей справедливо равенство: ;

-уравнение для совершенно аналогично уравнению для ;

-уравнение для – это уравнение, описывающее движение D-частиц в радиальном, фиктивном к D–миру измерении;

-движение D- частиц в фиктивном трехмерном пространстве происходит в центральном поле;

-на D-частицы действуют две силы: сила притяжения и сила отталкивания ;

-записав уравнения для и учитывая, что , D-наблюдатель сможет написать и понять смысл каждого из уравнений (П.62)-(П.66). В частности, он поймет, что космологические силы отталкивания в D-мире являются центробежными по своей природе. Они связаны с дисперсией скоростей D-частиц и кривизной двухмерного D-пространства.
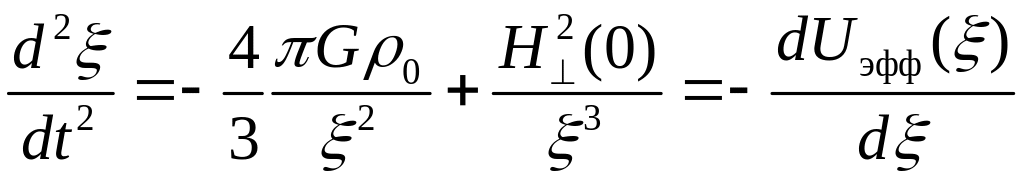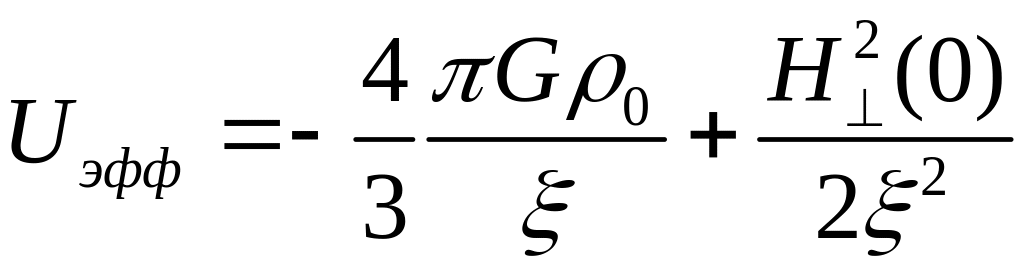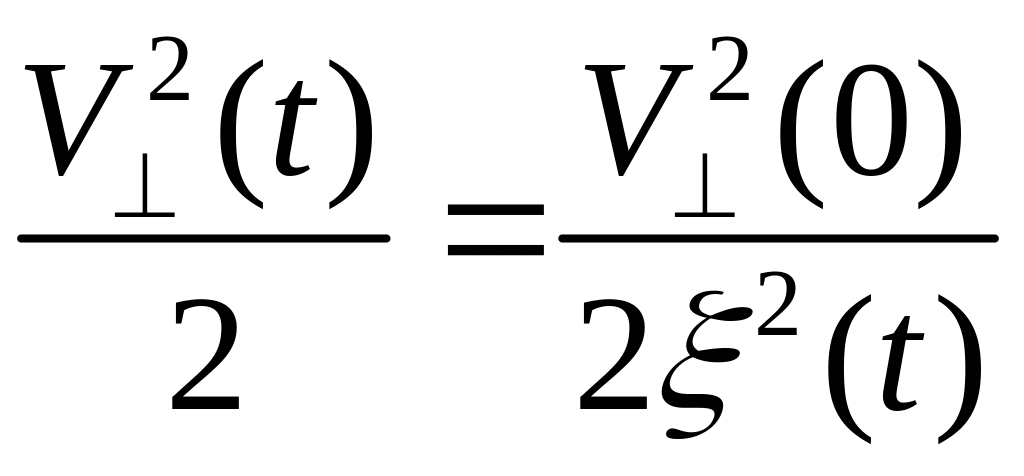