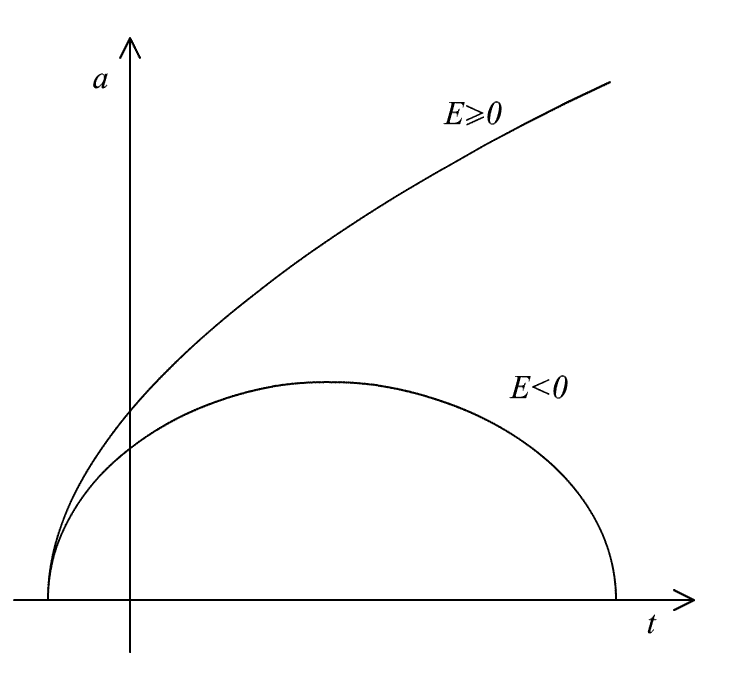Общие замечания

Вследствие предполагаемых начальных условий, а так же бесстолкновительности системы, все частицы относительно центра в радиальном направлении движутся одинаково. Они все время остаются равноудаленными от центра сферы, у них одинаково меняются продольная и поперечная компоненты скорости. Частицы однородно заполняют сферу переменного радиуса .

Частицы, удовлетворяющие указанным условиям, для краткости будем называть D–частицами, а однородную и изотропную сферическую гравитирующую оболочку, состоящую из D–частиц, будем называть 2D–миром. 2D-мир, по существу, является упрощенным двухмерным аналогом реального мира. Индекс 2 перед буквой D, обозначающий размерность рассматриваемой двухмерной гравитирующей системы, будем далее, для краткости, опускать.

Движение D–частиц происходит в центральном поле, поэтому сохраняются их вращательные моменты движения, а траектории частиц являются плоскими. Плоскость движения любой D–частицы содержит центр сферы (см., например,[25]).

Системы координат

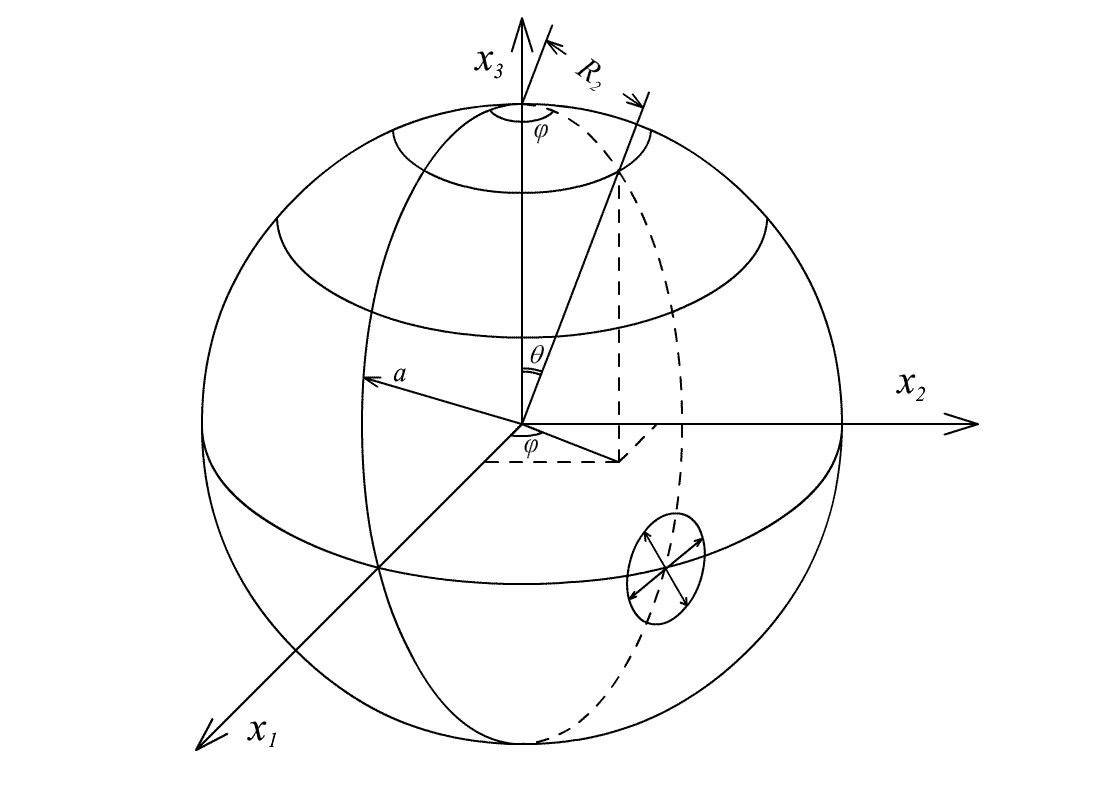
Динамику D–мира можно описывать, используя различные системы координат. На рис.16. приведены некоторые из них. Динамику D–мира удобно рассматривать в трехмерной сферической системе координат ( ). В то же время, его динамику, с точки зрения D–наблюдателей, естественно описывать, используя двухмерную, «внутреннюю» для них полярную систему координат ( ). Эту систему координат будем называть системой D–наблюдателей.

D–наблюдатель – это некоторый абстрактный объект, постоянно находящийся на гравитирующей сфере и совершающий относительно ее центра лишь радиальные движения. Система отсчета D–наблюдателей – это бесконечное их множество, равномерно и непрерывно заполняющее D–мир. Система отсчета D–наблюдателей является сопутствующей системой координат.

Динамика d – мира в сферической системе

Уравнения, описывающие D–мир в ньютоновском приближении в сферической системе координат ( ), очевидно, могут быть записаны в виде:

,	(П.47)
,	(П.48)
,	(П.49)

Индекс ноль здесь и далее относится к величинам, заданным в начальный момент времени t₀. Для простоты полагаем, что t₀=0.

Уравнение (П.47) описывает закон сохранения числа частиц. Закон сохранения вращательного момента частиц описывается уравнением (П.48). Уравнение (П.49) является уравнением, описывающим радиальное движение любой D–частицы в центральном поле (см. пункт «Уравнение, описывающее радиальное движение D- мира»). Решения этого уравнения удовлетворяют начальным условиям:

.

(П.50)

Используя обозначения:

, , , ,

(П.51)

уравнения (П.49), (П.50) после некоторых преобразований запишем в виде:

,	(П.52)
, .	(П.53)

Рис. 16. Системы координат, удобные для описания D–мира. – «внешняя», фиктивная для D–мира сферическая система координат. – «внутренняя» для D–мира, полярная система координат. – декартова система координат.

Из (П.52), (П.53) видно, что динамика D–мира в ньютоновском приближении определяется заданием трех параметров:

, и .

(П.54)

D–миры могут отличаться размерами , но при одинаковых значениях параметров (П.54) их динамика будет подобной. Уравнение (П.52) удобно записать в виде:

,

(П.55)

где

(П.56)

Это уравнение аналогично уравнению, описывающему одномерное движение частицы в потенциальном поле (см., например, §14 [25]). Используем эту аналогию для качественного анализа решений уравнения (П.55).

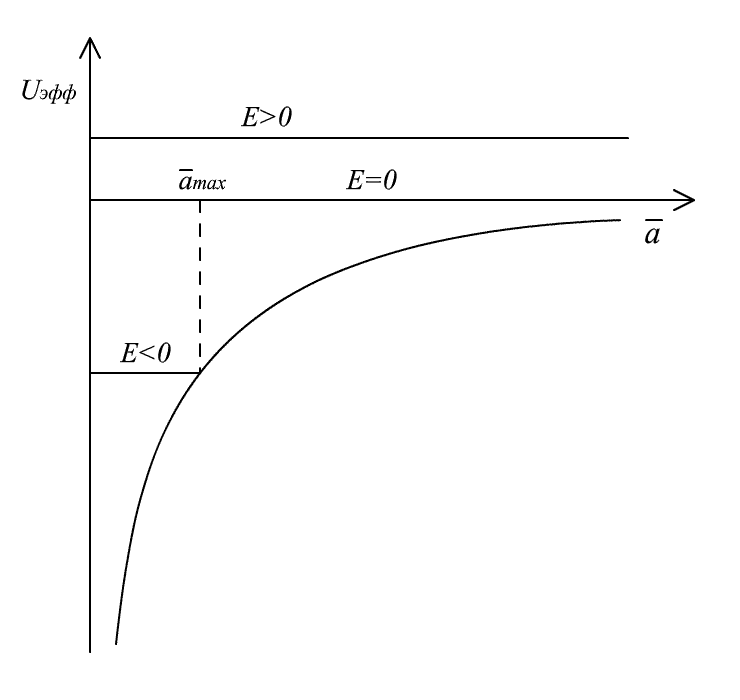
На Рис.17. и Рис.18. приведен вид функций , для случаев и . В зависимости от значений параметров (П.54) возможны различные типы решений, описывающих D–миры.

Параметром, определяющим характер эволюции D–мира, является энергия E. Она является первым интегралом уравнения (П.55). Интегрируя это уравнение, находим:

.

(П.57)

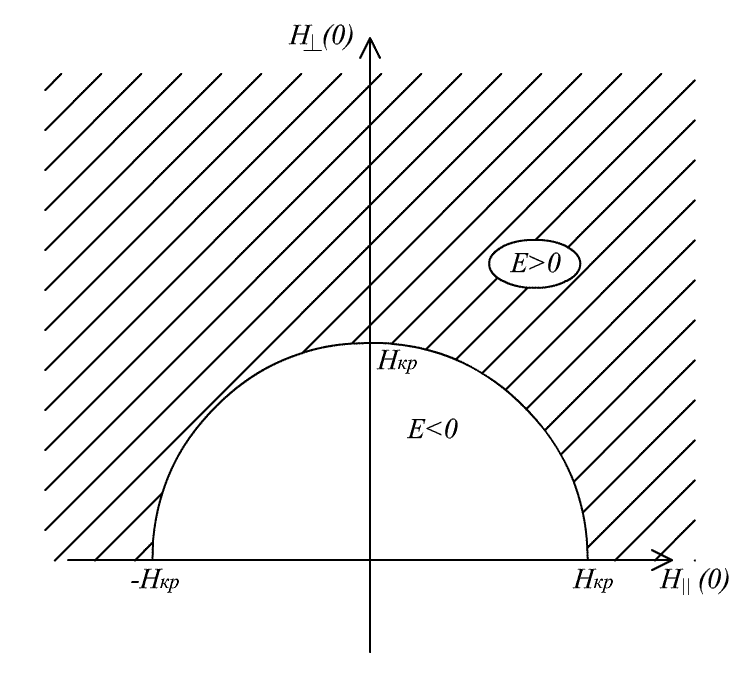
На рис.19. схематично изображены области параметров и для которых, при фиксированном значении , энергия 0 или , и D–миры имеют различный характер эволюции.

Используя начальные условия, энергию можно записать в виде:

,

(П.58)

где

.

(П.58)

Рис. 17. Вид функции при . Рис. 18. Вид функции при .

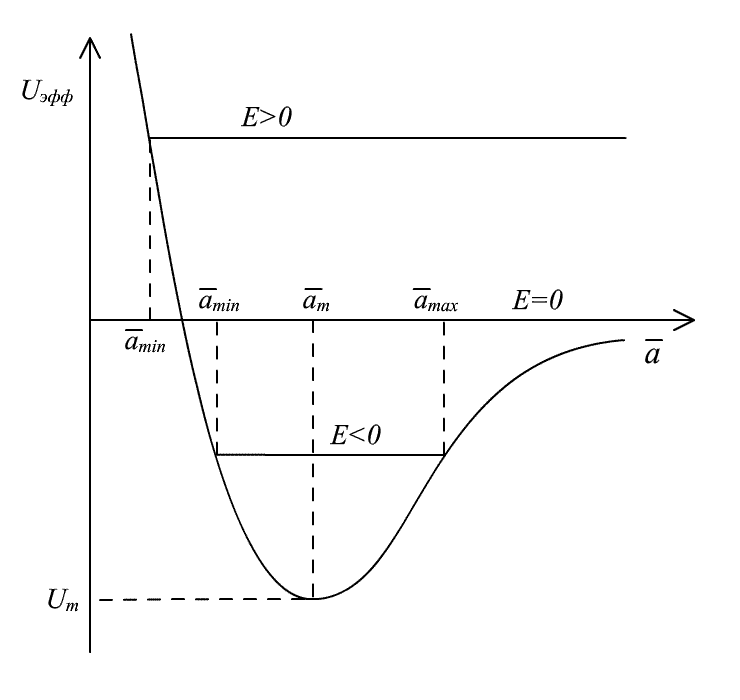
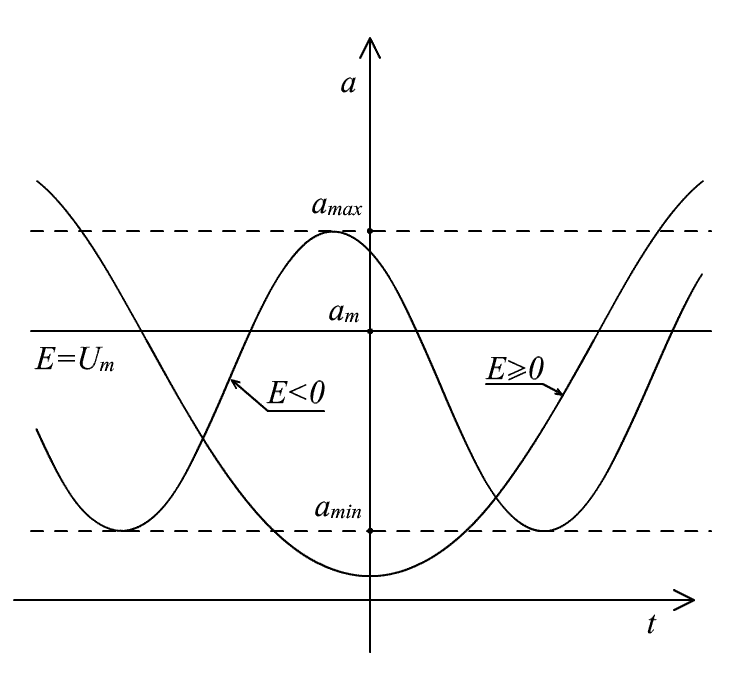
Характер эволюции D–миров при E<0  и схематично изображен на Рис.20. и Рис.21.

На эволюцию D–мира существенно влияет параметр , определяющий дисперсию скоростей D–частиц. Его влияние аналогично влиянию параметра . При даже вначале покоящийся D–мир, расширяясь, уйдет на бесконечность. Если , то решения, описывающие D–мир, не имеют сингулярности. При E<0 имеет место осцилляторная динамика D–мира. Область изменения : , где и – корни уравнения .

Рис. 19. Области параметров и для которых энергия или и D–миры имеют различный характер эволюции; .

При _E≥0 уравнение (рис.18.) имеет лишь один действительный корень . В этом случае область изменения : .

Как при E<0, так и при _E≥0, в области  расширение D–мира происходит с ускорением, а при с замедлением. Ускоренного режима расширения D–мира в области значений больших чем , в рассматриваемой нами модели, нет. Учитывая (П.57) и (П.58), заключаем, что асимптотическое значение радиальной скорости расширения, при и определяется формулой:

.

(П.60)

Рис. 20. Типы решений, описывающие D–миры, при . Финитный D–мир (E<0); Инфинитный D–мир (E≥0). Рис. 21. Типы решений, описывающие D–миры при Осциллирующий D–мир (E<0); Стационарный D–мир (E=Um); Инфинитный D–мир (E≥0).