8.3. Угловые размеры удаленных объектов
Формула, определяющая угол
,
под которым виден объект, имеющий размер
d и красное смещение
z, может быть
записана в виде:
|
(8.6) |
,
см. 4,7 [7]. В этой формуле r(z)
– расстояние до наблюдаемого объекта.
Учитывая, что физический размер объекта,
испускающего фотоны в момент времени
равен
,
отношение
,
а
,
а также измеряя длины в единицах
,
(8.6) запишем в виде:
|
(8.7) |
,
где
,
.
В ΛCDM- модели
вычисляется по формуле (7.18). Для того,
чтобы ΛCDM- модель давала
правильное значение для углов, под
которыми видны яркие пятна на однородном
фоне реликтового излучения, приходится
считать, что пространство является
плоским и полагать параметр
[6, 7]. Учитывая это, формулу (7.18) запишем
в виде:
|
(8.8) |
.Параметры, входящие в (8.8) связаны соотношением:
|
(8.9) |
,см. (7.19). Параметр в ΛCDM- модели вычисляем по формуле:
|
(8.10) |
.В расчетах h полагаем равным 0.7. С учетом (8.9), (8.10), заключаем, что в (8.8) независимым является лишь один параметр. Удобно считать, что им является параметр .
В С- модели
вычисляется по формуле (7.23). Независимыми
параметрами, входящими в (7.23) являются
,
и
(см. пункт 6.3). Приближение плоской
Вселенной, когда
полагается равным нулю, в С- модели не
используется. Для этого, как мы полагаем,
при наблюдениях объектов с
нет оснований.
Если бы пространство было плоским и
стационарным (евклидовым), а размер
наблюдаемого объекта был d,
то очевидно, что
определяло бы угол, под которым этот
объект в этом пространстве наблюдался
бы с расстояния
(считаем, что
<<1).
Величина определяет расстояние, которое проходят фотоны за время . Величина определяет возраст Вселенной. Она достаточно точно определяет также время свободного движения фотонов после рекомбинации, поскольку время между Большим взрывом и рекомбинацией много меньше времени .
Угол
будем обозначать величиной
.
Значок Е обозначает, что этот угол
вычислен в приближении плоского
стационарного евклидова пространства.
С учетом обозначения
формулы, определяющие углы
в ΛCDM- и в С- модели, запишутся
в виде:
|
(8.11) |
|
(8.12) |
,
.
Как видно из (8.7), для того, чтобы определить
угол
,
необходимо знать величины
и
.
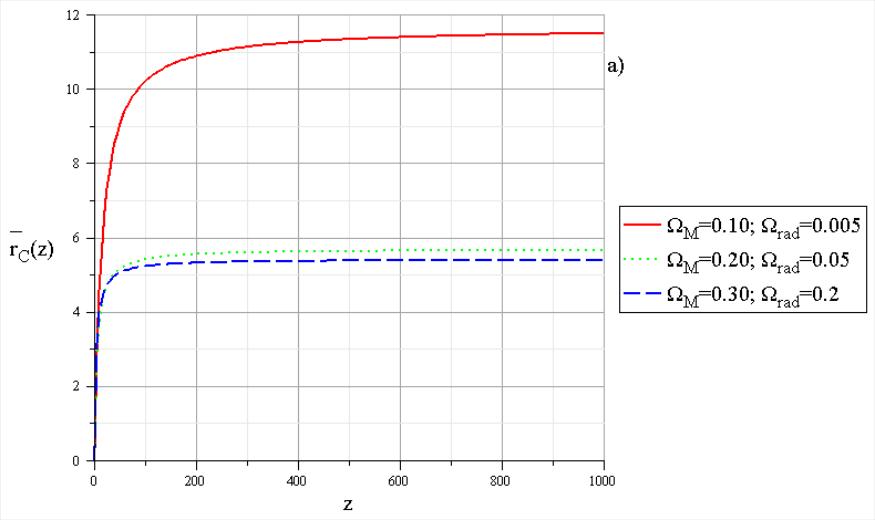
На рис.15.а) приведены графики функции
для случаев (8.5). Видно, что значения
при
в рассматриваемых случаях отличаются
существенно. Вычисление
проводилось по формуле (7.23) для
.
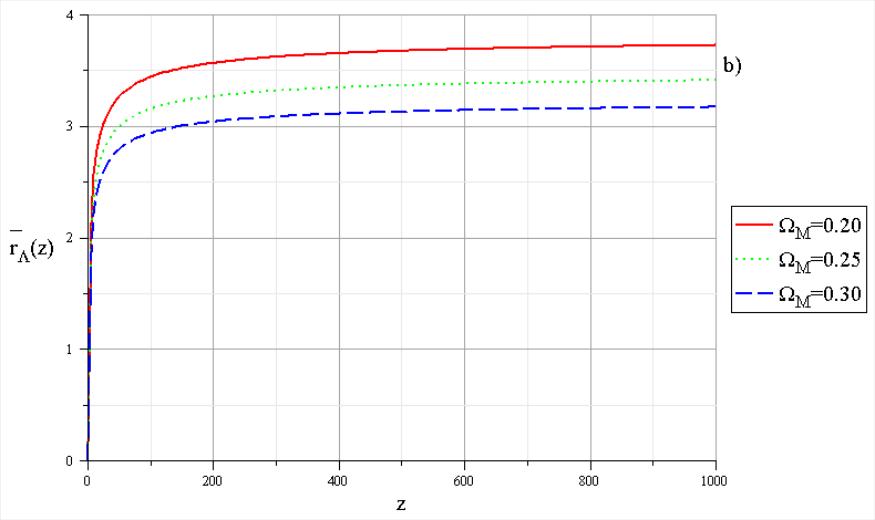
Графики зависимости для значений , рассчитанные в рамках ΛCDM-модели по формуле (8.8), приведены на рис.15.b). Приведенные графики построены для трех случаев. Им соответствуют следующие значения параметров ΛCDM-модели:
|
(8.13) |
,
,
,
;
,
,
,
.Из рис.15.b) видно, что значения при для случаев (8.13) отличаются заметно.
Из рис.15.a) и 15.b)
видно, что в области значений
зависимости
и
выходят на насыщение и практически не
зависят от z.
При расчетах угла считаем, что рекомбинация имела место при z=1100.
Время жизни Вселенной
для каждого из рассматриваемых случаев
(8.5), (8.13), находим из условия:
.
В расчетах полагаем, что современной
Вселенной соответствует τ=0.
Возраст Вселенной, согласно С-модели, оказывается равным:
1.45·1010 лет; 1.41·1010 лет; 1.37·1010 лет |
(8.14) |
для случаев 1), 2) и 3) (см. (8.5)), соответственно.
Согласно ΛCDM-модели соответствующие возрасты Вселенной оказываются равными:
1.51·1010 лет; 1.42·1010 лет ; 1.35·1010 лет |
(8.15) |
для случаев 1), 2) и 3) (см. (8.13)), соответственно.
Расстояние d, входящее
в формулу (8.6), существенным образом
зависит от параметров модели. Согласно
[32], [33], расстояние d
определяется возрастом Вселенной в
момент рекомбинации. Далее этот возраст
обозначаем как
.
Этот возраст в каждом из рассматриваемых
случаев (8.5) и (8.13) оказывается своим.
Возраст
находим из условия:
.
Считаем, что
.
Возраст согласно С-модели оказывается равным:
2.56·106 лет; 8.07·105 лет; 4.04·105 лет |
(8.16) |
для случаев 1), 2) и 3) (см. (8.5)), соответственно.
Согласно ΛCDM-модели, возраст оказывается равным:
4.16·105 лет; 3.72·105 лет; 3.39·105 лет |
(8.17) |
для случаев 1), 2) и 3) (см. (8.13)), соответственно.
Размер d, определяющий расстояние между центрами соседних пятен в момент рекомбинации вычисляем по формуле:
|
(8.18) |
.
Рис. 15. Зависимость в С-модели a) и в ΛCDM-модели b) при больших значениях z. |
Учитывая (8.18), формулу (8.6), определяющую угол запишем в виде:
|
(8.19) |
.
Используя эту формулу, находим углы
для случаев (8.5) и углы
для случаев (8.13). Они оказываются равными:
2.008; 1.285; 0.675 |
(8.20) |
для случаев 1), 2) и 3) (см. (8.5)) С-модели и
1.004; 0.981; 0.963 |
(8.21) |
для случаев 1), 2) и 3) (см. (8.13)) ΛCDM-модели. Значения углов приведены в градусах.
Наблюдения показывают, что характерное угловое расстояние между соседними яркими пятнами на равномерном фоне реликтового излучения равно одному градусу (с точностью до 2%) (см. [6],[7]). Из (8.21) видно, что ΛCDM-модель с параметрами 2) (см. (8.13)) достаточно точно определяет угловые размеры наблюдаемых пятен. Эти параметры ΛCDM-модели являются хорошими также и для объяснения наблюдений в области (см. §7).
Из (8.20) видно, что есть основания считать, что С-модель с правильно подобранными значениями параметров и , также даст правильное значение углового расстояния между яркими пятнами на равномерном фоне реликтового излучения.