7.2. Зависимость в λcdm- модели

Для расчета зависимости , предварительно вычисляем функцию . Учитывая (7.5), (7.6) и (5.29), формулу, определяющую расстояние до наблюдаемого объекта, имеющего красное смещение z, запишем в виде:

.

(7.18)

Параметры , , и не являются независимыми. Из (5.29), (5.31) следует:

.

(7.19)

Далее, учитывая, что [7] и предполагая применение модели в области не слишком больших , влиянием релятивистской компоненты на гравитационное космологическое ускорение пренебрегаем. Формально это означает, что в расчетах полагаем равным нулю.

Обычно для интерпретации наблюдений используется «плоская ΛCDM- модель » в которой полагают .

Считая, что , , формулы (7.18), (7.19) записывают в виде:

,	(7.20)
.	(7.21)

Если согласиться, с утверждением о «плоскостности» пространства и полагать , а так же пренебрегать влиянием релятивистской компоненты на динамику Вселенной, то параметрами, определяющими , а, следовательно, и зависимость в ΛCDM- модели, являются и , причем вследствие соотношения (7.21) независимым является лишь один из них, например, .

В «плоской» ΛCDM- модели чем больше значение , тем меньше , т.е. тем больше влияние сил гравитации и тем меньше влияние сил отталкивания.

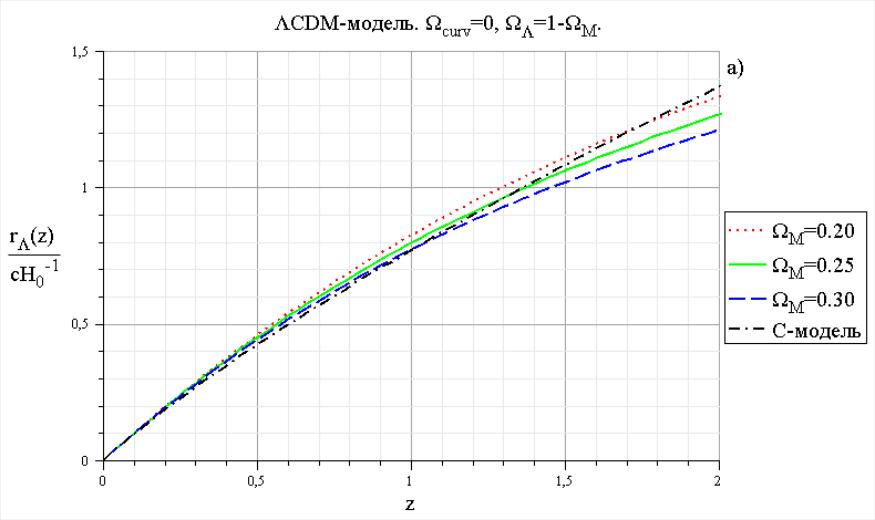
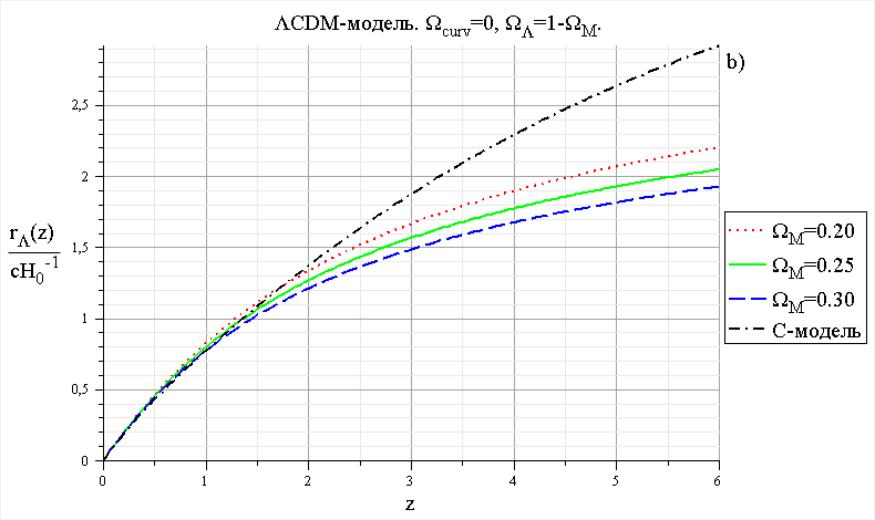
На рис.9. приведены графики зависимости для значений и в интервале от 0.2 до 0.3 с шагом 0.05. Соответствующие значения взяты равными . Выбор интервала для связан с учетом современных предположений о наиболее вероятном значении этого параметра. Эти предположения основаны на практике применения ΛCDM- модели для интерпретации различных наблюдательных данных (см., например, [6, 7, 16, 17, 18]).

При различие расстояний , соответствующих различным значениям параметров и , несущественно. Однако при оно становится заметным, а при значительным. Видно, что чем меньше и, соответственно, больше , тем больше при заданном z расчетное значение . Это означает, что чем больше влияние сил отталкивания, тем дальше согласно ΛCDM- модели находятся объекты с заданным z и тем меньше их видимая яркость. Именно это и пытаются обнаружить в реальных наблюдениях сверхновых типа Ia [3, 4, 17, 18].

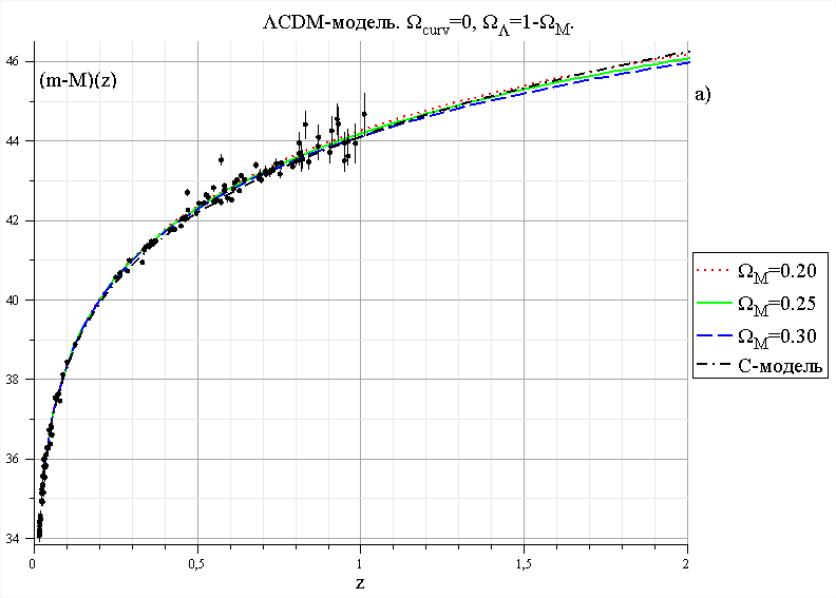
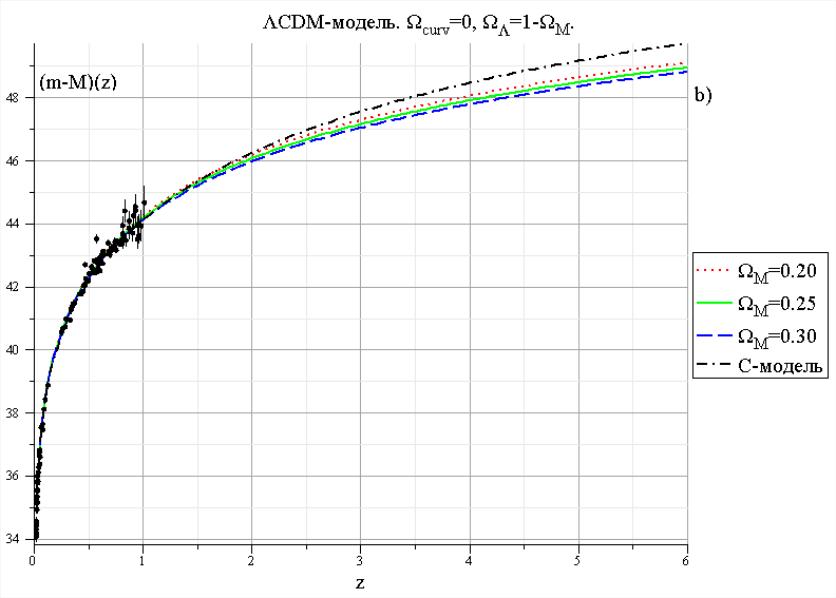
На рис.10. приведены графики зависимости , рассчитанные по формуле (7.12) с использованием значений функции , вычисленных для тех же значений и , что и на рис.9. Сравнение теоретически рассчитанных в рамках ΛCDM- модели зависимостей с наблюдаемой для сверхновых типа Ia (см. рис.10.), показывает, что «плоская» ΛCDM- модель , если считать, что значение параметра , а , качественно правильно описывает изменение при . Стандартная математическая процедура выбора теоретически рассчитанной зависимости , наилучшим образом описывающей наблюдательные данные в области , показывает, что это имеет место при , , см., например, [16- 19].

В то же время утверждать, что именно эти параметры близки к реальным, а ΛCDM- модель является правильной, преждевременно. Это связано со следующими причинами.

1. Велики погрешности в определении величины . В то же время теоретически рассчитанные функции даже с заметно отличающимися значениями параметров , , в области красных смещений различаются мало. Но именно к этой области значений z и относятся наблюдаемые сверхновые.

2. Правильная модель должна объяснять наблюдения не только относящиеся к области 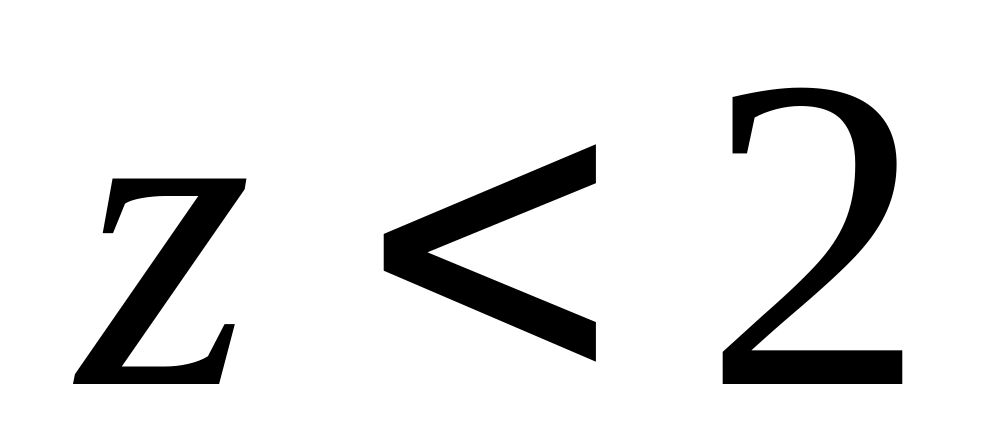, но и для любых других . В том числе, объяснять наблюдения относящиеся к .

3. Де-Ситтеровские решения, являющиеся асимптотиками для решений ΛCDM-модели при , на наш взгляд не являются физически разумными.

Согласно ΛCDM- модели ускоренное расширение Вселенной имеет место при выполнении неравенства: (см. (5.32)). Если предполагать, что , а , то упомянутое выше неравенство выполняется с большим запасом. Это означает, что согласно ΛCDM- модели современная Вселенная расширяется с ускорением. Поскольку ΛCDM- модель лежит в основе интерпретации наблюдательных данных, то это и явилось основанием для утверждения об ускоренном расширении Вселенной [3, 4]. В настоящее время мнение о том, что Вселенная расширяется ускоренно является практически общепринятым, см., например, [6, 7, 17, 18].

Рис. 9. Зависимость в ΛCDM- модели. Приведен также график сравнения для С-модели с параметрами и . Приведены графики для следующих значений параметров: , от 0.2 до 0.3 с шагом 0.05; . Области изменения : а) ; б) .

Рис. 10. Зависимость в ΛCDM- модели. . Приведен также график сравнения для С-модели с параметрами и . Приведены графики для следующих значений параметров: , от 0.2 до 0.3 с шагом 0.05; . Области изменения : а) ; б) . Вертикальные черточки на рисунке определяют неопределенность значений наблюдаемых величин , связанную с ошибками измерений. Наблюдательные данные взяты из [17].

Согласно ΛCDM- модели в прошлом при достаточно больших z, когда условие не выполнялось, Вселенная расширялась с замедлением ( ). Из (5.32) видно, что переход от замедленного расширения к ускоренному произошел при [7]:

.

(7.22)

Зависимости и для значений параметров , и от 0.2 до 0.3 с шагом 0.05, , полученные численным решением уравнения (5.33) с граничными условиями (5.34), приведены на рис.5а. и рис.5б.

Видно, что при , значение достигается при . Это означает, что возраст Вселенной при этих значениях параметров и оказывается приблизительно равным лет. Переход к режиму ускоренного расширения, для значений параметров и , как видно из рис.5б, произошел при то есть приблизительно лет назад.
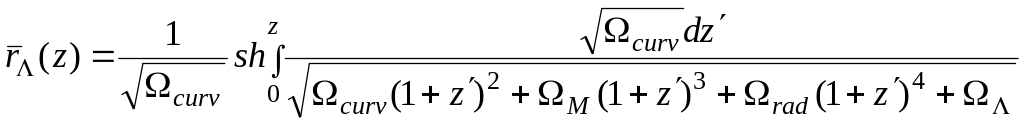