6.3. Возможные варианты эволюции Вселенной в с- модели
Параметрами, определяющими характер эволюции Вселенной в рамках С- модели являются:
,
,
|
(6.17) |
.Эти параметры, не являются независимыми. Из уравнения (5.24), с учетом граничных условий (5.34), находим соотношение между ними:
|
(6.18) |
.Параметры и связаны с параметрами , и соотношениями (5.29). Учитывая это, из (6.18) заключаем, что в С-модели независимыми являются лишь два параметра. Удобно считать, что этими параметрами являются и .
Опыт применения С- модели для интерпретации наблюдательных данных отсутствует. Работа по выбору оптимальных значений параметров С- модели не проведена. Полагать, что значения аналогичных параметров в С- и ΛCDM- моделях совпадают нет оснований. Значения параметров в ΛCDM- модели взяты не из непосредственных измерений, а являются, в основном, результатом подгонки параметров модели под наблюдения. Выбор параметров С- модели, как и параметров ΛCDM- модели, должен производится с учетом ее наилучшего соответствия наблюдениям.
Уравнение (5.25), определяющее изменение характерного масштаба в С- модели, запишем в виде:
|
(6.19) |
,где
|
(6.20) |
.Уравнение (6.19) используем для качественного анализа его решений. Учитываем, что это уравнение аналогично уравнению, описывающему одномерное движение частицы в потенциальном поле (см., например, §11 [25]).
Интегрируя (6.19) с начальными условиями (5.34), находим его первый интеграл- энергию:
|
(6.21) |
.Используя начальные условия (5.34), а так же (6.18), находим константу интегрирования:
|
(6.22) |
.
На рис.6. схематически изображен график
функции
,
для значений параметра
>1.
На этом же рисунке, для сравнения,
приведен график
.
Используя стандартную методику анализа решений уравнения, описывающего одномерное движение частицы в потенциальном поле и учитывая графики зависимости и , заключаем, что возможны три типа решений уравнений (6.13), (6.19), описывающих динамику Вселенной в рамках этих моделей.
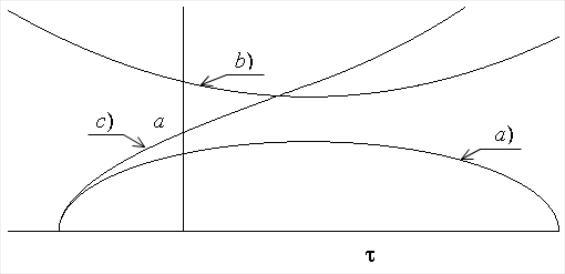
В этом пункте рассмотрим решения,
описывающие С- модель. Графики, качественно
изображающие различные типы этих
решений, описывающие С- модель при
изображены на рис.7.
Если
,
то реализуются решения типа a).
Они описывают замкнутую Вселенную,
имеющую конечную массу и объем. В этих
решениях силы гравитации во все моменты
эволюции Вселенной играют определяющую
роль. Расширение Вселенной происходит
с замедлением. После достижения
максимального размера Вселенная начинает
сжиматься, повторяя динамику расширения,
но в обратном направлении.
Рис. 6. Схематические графики функций
и
.
1-
;
2-
,
|
.
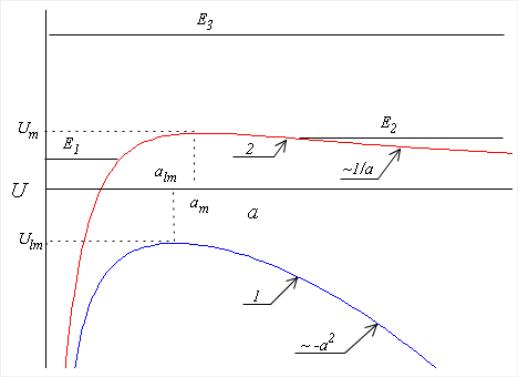
Рис. 7. Возможные типы решений уравнения
(6.19), описывающего динамику Вселенной
в С- модели при значениях параметра
.
a)
|
,
–
замкнутая Вселенная;
b)
,
–
открытая Вселенная без сингулярности;
c)
–
открытая Вселенная с сингулярностью.
При
,
реализуются решения типа b).
Они описывают открытую Вселенную,
имеющую бесконечную массу, а также
бесконечный объем. В решениях этого
типа космологические силы отталкивания
всегда больше сил притяжения. Отсутствует
сингулярность. В решениях типа b),
значение
может быть достаточно малым и «остановка»
Вселенной происходит при очень большой
плотности и температуре космической
среды. Объемные центробежные силы
отталкивания при этом оказываются
достаточными, чтобы воспрепятствовать
гравитационному сжатию Вселенной в
сингулярное состояние. В то же время
отметим, что исследование динамики
Вселенной в области температур и
плотностей, при которых двухкомпонентное
приближение может перестать быть
правильным, потребует уточнения С-
модели и отдельного детального анализа.
В настоящей работе он не проводится.
Если
,
то реализуются решения типа с). Они
описывают открытую Вселенную, у которой
бесконечны и масса, и объем. Эволюция
этой Вселенной начинается из сингулярного
состояния. В области
главными являются силы притяжения. При
этих
Вселенная расширяется с замедлением.
При
силы притяжения и отталкивания
сравниваются по величине. В области
силы отталкивания становятся главными.
Расширение Вселенной происходит с
ускорением. Если при
скорость расширения Вселенной мала, то
в окрестности
будет иметь место длительная «задержка
развития» Вселенной.
Решения как типа b), так и типа с), позволяют объяснить ускоренное расширение Вселенной. Но какое из них описывает реальную Вселенную? Полагаем, что скорее всего им является одно из решений типа c). В решениях типа b) силы отталкивания во все времена больше сил притяжения и поэтому, как мы полагаем, отсутствуют условия для роста таких структур, как галактики и их скопления. Эти решения могли бы описывать бесструктурную Вселенную.
Начальный период эволюции Вселенной,
при
,
ΛCDM- и С-моделью описывается
одинаково. В то же время динамика,
рассчитанная в рамках этих моделей, для
современной Вселенной и ее будущего,
оказывается различной. Это связано с
тем, что силы отталкивания в этих моделях
описываются по-разному.
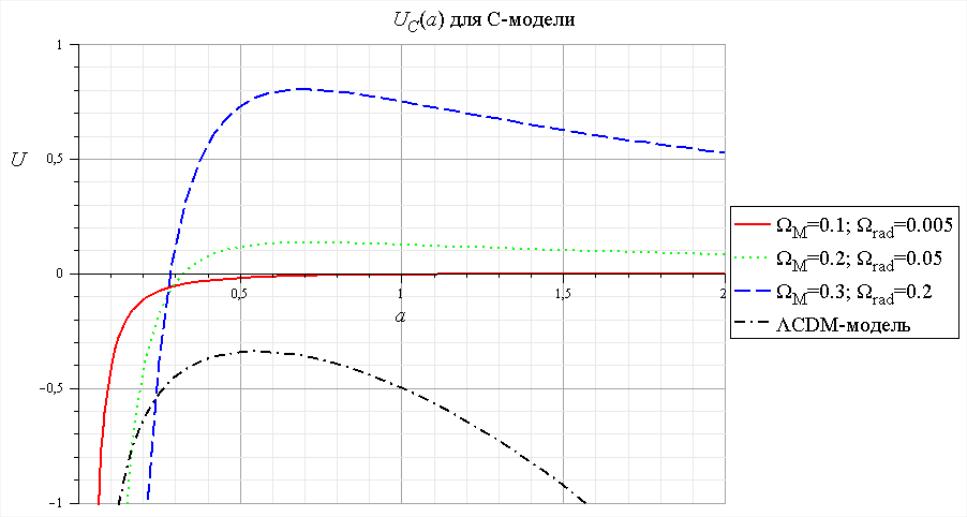
На рис.8. приведены графики
для различных значений параметра
.
Приведен так же график зависимости
для наиболее вероятных значений
параметров ΛCDM- модели.
Видно, что существенные различия в
зависимостях
и
могут иметь место в области
.
Это имеет место, если в С- модели значение
параметра
,
а
»
10-4. Отметим так же, что
характер поведения функции
при
в области малых значений
,
существенным образом зависит от величины
параметра
.
Силы притяжения в ΛСDМ
- модели и С-модели во все времена,
описываются одинаково. На ранних стадиях
эволюции Вселенной в эпоху доминирования
релятивистской компоненты, когда
эти силы играют определяющую роль (см.
рис.3). (Напомним, что значения параметра
в С- и ΛCDM- моделях существенно
отличаются). В литературе эпоху
доминирования релятивистской компоненты
обозначают как RD-эпоха,
см., например, [1].
Рис. 8. Графики, определяющие функцию
для различных значений параметров
и
.
Приведен так же график «потенциала»
для наиболее вероятных значений
параметров ΛСDМ-
модели
|
.
Уравнение, описывающее изменение линейных масштабов Вселенной в RD- эпоху, как в С-модели, так и ΛСDМ-модели, имеет вид:
|
(6.23) |
.Это уравнение имеет решение
|
(6.24) |
Вселенная расширяется с замедлением.
В RD- эпоху
.
Изменения во времени плотности энергии
,
давления P и температуры
Т космической среды в RD-
эпоху описываются соотношением:
~ P ~ T4 ~ 1/t2. |
(6.25) |
Закономерности протекания физических процессов в горячей Вселенной в эпоху преобладания релятивистской компоненты хорошо изучены (см., например, [1, 2, 6, 7]). Надежно установленные выводы современной космологии, касающиеся природы реликтового излучения, а также первичного состава космической среды, существенным образом связаны с закономерностями эволюции Вселенной на ранних стадиях. В рамках С-модели они могут быть объяснены также как и в рамках ΛСDМ-модели. Самые ранние стадии эволюции Вселенной в этих моделях описываются одинаково.
В процессе эволюции Вселенной, плотность
массы релятивисткой компоненты (
)
падает, с увеличением характерного
масштаба a, существенно
быстрее, чем плотность нерелятивистской
компоненты (
)
и поэтому, как показывают расчеты в
рамках ΛСDМ-
модели, RD-эпоха закончилась
достаточно быстро. Это имело место
приблизительно через восемьдесят тысяч
лет после начала расширения Вселенной
[7].
Чтобы в рамках С- модели объяснить ускоренное расширение Вселенной, необходимо считать, что Вселенная существенно более релятивистская, чем это предполагается в современной космологии. Необходимо предполагать, что значение параметра »10-4. При этом влияние релятивистской компоненты на динамику Вселенной и по длительности и по интенсивности существенно больше, чем это считается в ΛCDM- модели. Длительность RD-эпохи в С-модели зависит от параметров и .
Согласно С- модели, именно релятивистская
компонента и определяет космологические
силы отталкивания во Вселенной. В тоже
время, как и в ΛCDM-модели,
согласно С-модели уже давно
и поэтому в современной Вселенной
определяющую роль в создании гравитационного
поля играет нерелятивистская компонента,
а вклад релятивистской компоненты
является пренебрежимо малым.
В литературе часто времена, когда определяющую роль в создании гравитационного поля играет нерелятивистская компонента называют пылевидной стадией, см., например, [7]. В ΛCDM-модели время перехода от RD-эпохи к пылевидной стадии лежит в области семидесяти - девяноста тысяч лет после Большого взрыва. В С-модели возраст Вселенной во время перехода от RD-эпохи к пылевидной стадии существенным образом зависит от значения параметров и . Он заметно больше, чем соответствующий возраст в ΛCDM-модели. Его значение может быть установлено, когда будут найдены параметры и С-модели при которых она правильно описывает эволюцию Вселенной.
Будущее Вселенной, предсказываемое
ΛCDM- моделью [6, 7], описывается
де- Ситтеровскими решениями, в которых
.
В С-модели особенность в поведении
скорости расширения Вселенной при
отсутствует. Она предсказывает плавный
переход Вселенной в будущем в стадию
равномерного расширения со скоростью:
|
(6.25) |
.
Эта скорость лишь незначительно будет
превышать современное значение скорости
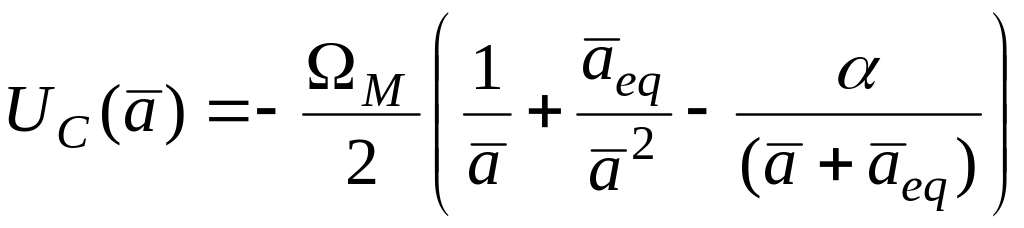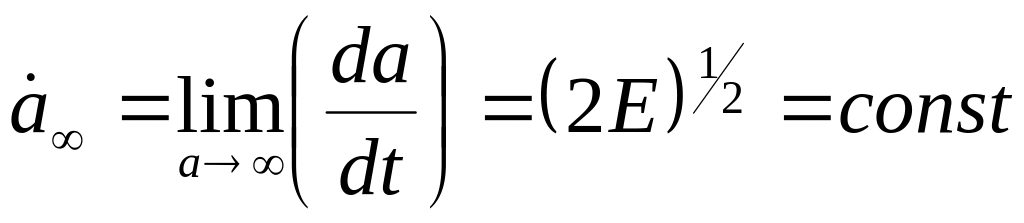