6.2. Сценарий эволюции Вселенной в λcdm- модели

Параметрами, определяющими характер эволюции Вселенной в рамках ΛCDM- модели являются:

.

(6.11)

Эти параметры, входящие в описание ΛCDM- модели, не являются независимыми. Из уравнения (5.31), с учетом граничных условий (5.34), следует:

.

(6.12)

Практика применения ΛCDM- модели для интерпретации наблюдательных данных существенно сузила область допустимых значений каждого из параметров (6.11).

Например, для того, чтобы в рамках ΛCDM- модели объяснить наблюдаемую анизотропию реликтового излучения, необходимо считать, что пространственная кривизна Вселенной или точно равна нулю, или весьма мала. Полагают, что наблюдаемая часть Вселенной с хорошей точность является пространственно плоской. Количественно в ΛCDM- модели это сводится к ограничению на величину , см., например, [6, 7]. Для интерпретации наблюдений, часто используется «плоская» ΛCDM- модель в которой полагают .

При использовании ΛCDM- модели учитывается, что отношение параметров и , определяющее соотношение плотностей релятивистской и нерелятивистской компонент в современной Вселенной, много меньше единицы ( см., например, [7]). Следствием малости отношения является часто используемое приближение . Формально оно означает пренебрежение влиянием релятивистской компоненты на динамику Вселенной. В рамках ΛCDM- модели это приближение является хорошим в области .

С учетом высказанных замечаний о значениях параметров (6.11) считают, что параметрами ΛCDM- модели, определяющими динамику Вселенной во все времена ее эволюции (за исключением ранней Вселенной, когда ) являются два: и . Учитывая (6.12), заключаем, что независимым, фактически является лишь один из них, например, . При этом .

Знание значений параметров (6.11), которые в ΛCDM- модели являются наиболее вероятными, позволяет существенно упростить практику применения этой модели для интерпретации наблюдений.

Уравнение (5.32), определяющее изменение характерного масштаба Вселенной в ΛCDM- модели, запишем в виде:

,

(6.13)

где

.

(6.14)

Уравнение (6.13) аналогично уравнению, описывающему одномерное движение частицы в потенциальном поле (см., например, §11 [25]). Используя стандартную процедуру, можно определить допустимые типы решений уравнения (6.13) не решая его аналитически или численно. Можно качественно изобразить вид функций , соответствующих возможным типам решений этого уравнения. В работе, ограничимся рассмотрением лишь той из них, которая, как полагают, правильно описывает наблюдения.

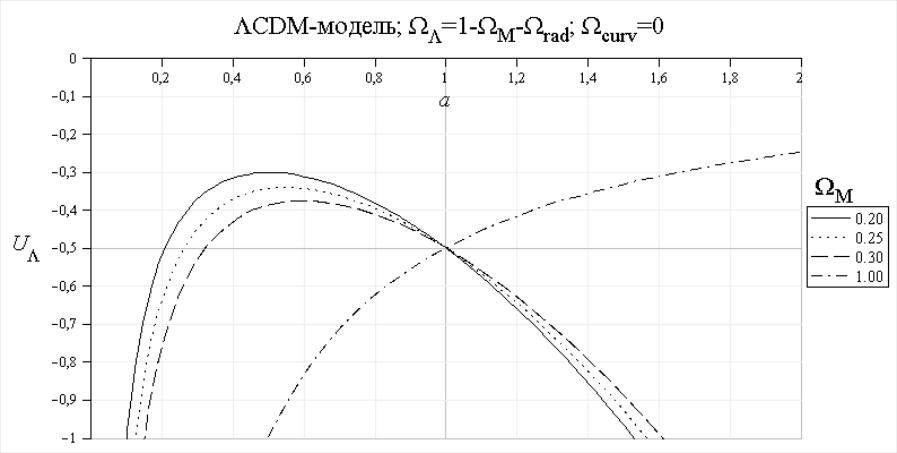
Рис. 4. Графики зависимости для некоторых вероятных значений параметров ΛCDM- модели. График, соответствующий значению , проведен для сравнения.

Интегрируя (6.13), находим его первый интеграл – энергию:

.

(6.15)

Учитывая начальные условия (5.34), а так же соотношение (6.12) находим константу интегрирования:

.

(6.16)

Приближение «плоской» ΛCDM- модели ( ) означает, что константу интегрирования полагают равной нулю.

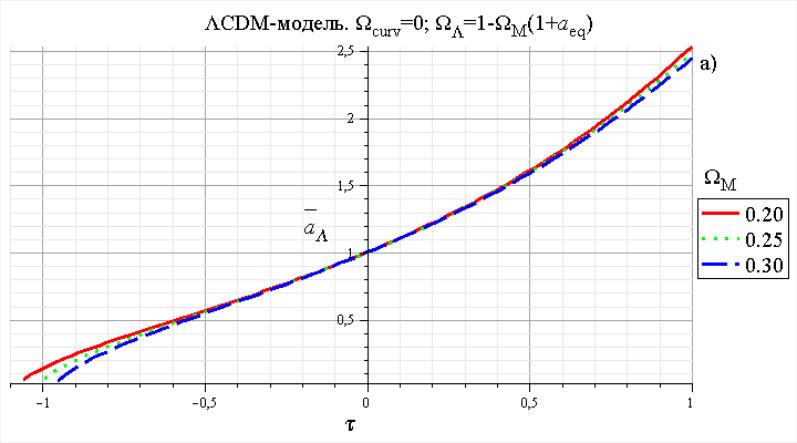
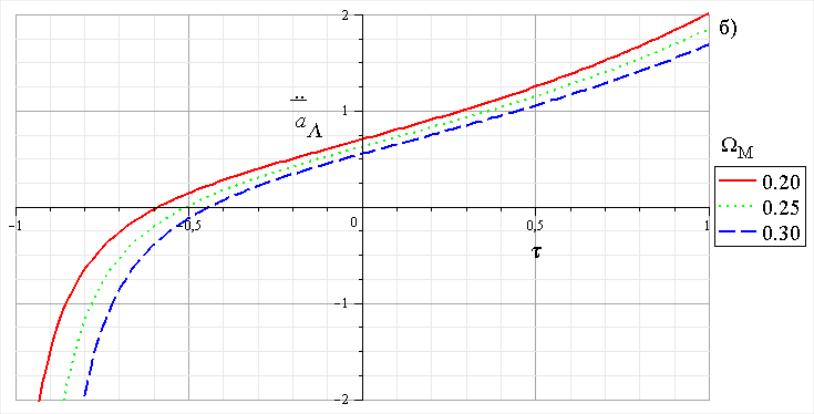
Рис. 5. Зависимости и в ΛCDM- модели. Приведены графики для следующих значений параметров: , : от 0.2 до 0.3 с шагом 0.05; ; .

На рис.4. изображены графики зависимости для значений , и в интервале от 0.2 до 0.3 с шагом 0.05. Выбор такого интервала для связан с учетом данных о наиболее вероятном значении этого параметра, основанных на практике применения ΛCDM- модели для интерпретации различных наблюдений. Значительные изменения (например, на порядок) параметра , который в расчетах полагается равным мало влияет на вид и соответствующие решения . Влияние этого параметра на решения имеет место лишь в области значений . Значительное увеличение параметра не приводит к качественному изменению решений , описывающих ΛCDM- модель.

На рис.5. изображены графики зависимостей и , найденные численным решением уравнения (5.32) с граничным условием (5.34). Приведены решения для тех же значений параметров модели, что и на рис.4.

Многочисленные применения ΛCDM- модели для интерпретации различных наблюдательных данных показывают, что, по-видимому, наиболее вероятными значениями параметров и являются: , см. [16-19]. При этих значениях параметров и , как видно из рис.5., согласно ΛCDM- модели, возраст Вселенной оказывается приблизительно равным . Первую половину этого времени Вселенная расширялась с замедлением. Последние приблизительно семь миллиардов лет она расширяется с ускорением. Согласно (6.6), в настоящее время космологические силы отталкивания значительно превосходят силы притяжения (приблизительно в шесть раз).
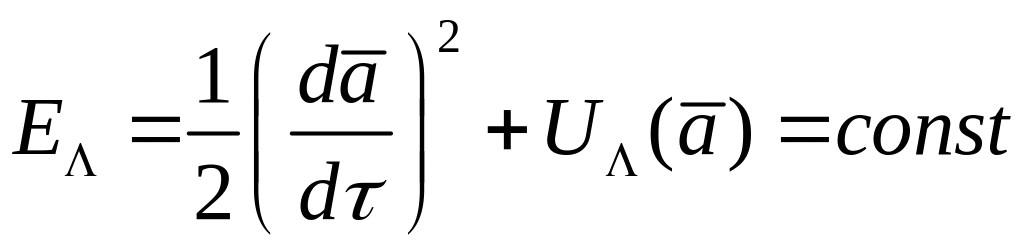