Параметры и

Хорошее согласие ΛCDM- модели с наблюдениями имеет место при значениях параметров

,

(5.44)

см. [16- 18]. Эти значения в значительной степени являются не результатом непосредственных измерений, а следствием подгонки параметров ΛCDM- модели с целью наилучшего объяснения наблюдательных данных. Возможно, что значение параметра в C-модели заметно отличается от предполагаемого в (5.44). В настоящей работе рассматривается такая возможность. Выбор значения параметра в С-модели производим на отрезке [0.10, 0.30]. Полагаем что лишь в процессе длительного и тщательного применения С-модели для объяснения различных наблюдательных данных, с учетом точности их измерения, можно будет определить наиболее вероятные значения параметров и этой модели при которых она правильно описывает динамику Вселенной.

Настоящая работа является лишь демонстрацией возможности использования предлагаемых нами сил отталкивания для объяснения наблюдаемой динамики Вселенной. Полагаем, что лишь практика применения С-модели для объяснения различных наблюдательных данных определит наиболее вероятные значения параметров и этой модели, при которых она правильно описывает динамику Вселенной.

§6. О решениях уравнений, описывающих λcdm- и с – модели

В этом параграфе качественно рассмотрены возможные типы решений уравнений, описывающих ΛCDM- и С- модели. Показано, какие эпохи эволюции Вселенной в этих моделях описываются одинаково, а какие различно.

В С- модели, также как и в ΛCDM- модели, учитываются данные о глобальных свойствах Вселенной, которые в настоящее время являются общепринятыми. Они обе являются моделями однородной изотропной Вселенной. Теоретической основой этих моделей являются космологические уравнения А.А.Фридмана.

Принципиальное отличие С- модели от ΛCDM- модели состоит в том, что так называемая «темная энергия» определяется в С- модели как известная тепловая энергия космической среды.

Для объяснения космологических сил отталкивания в С- модели используется гипотеза об их центробежной природе. В этой модели тепловая энергия является не только одним из источников гравитационного поля. Но и источником сил отталкивания.

В следующем пункте проведен сравнительный качественный анализ характера изменения космологических сил, определяющих динамику Вселенной в С- и ΛCDM- моделях.

6.1. О соотношении космологических сил притяжения и отталкивания в с- и λcdm- моделях

Описание сил притяжения в С- и ΛCDM- моделях одинаково, а сил отталкивания совершенно различно (см. уравнения (5.25), (5.32)).

Космологическое ускорение, создаваемое силами притяжения, определяется в обеих моделях формулой:

(6.1)

Формула, определяющая космологическое ускорение, создаваемое силами отталкивания в С- модели, имеет вид:

.

(6.2)

Соответствующее ускорение в ΛCDM- модели определяется формулой:

.

(6.3)

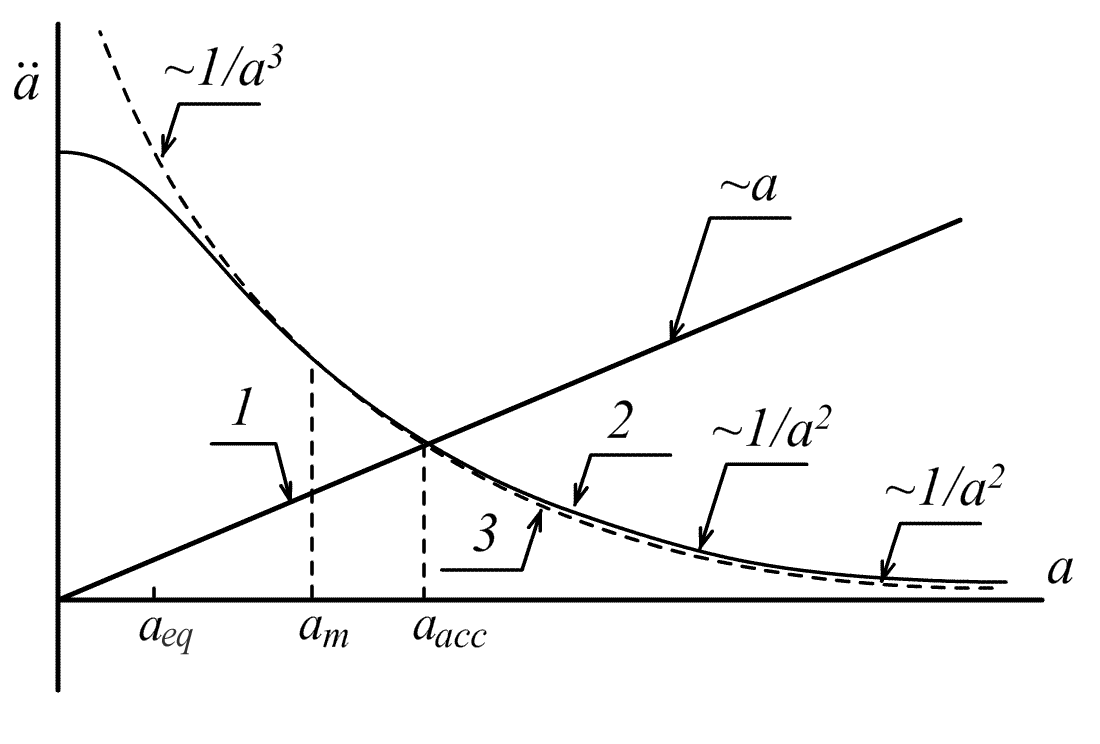
На рис.3. приведены графики, качественно характеризующие зависимости , и от радиуса кривизны Вселенной. Эти графики наглядно показывают в чем состоит принципиальное различие ΛCDM- и С- моделей.

Здесь и далее величины рассчитанные в рамках ΛCDM- модели будем обозначать индексом Λ, а величины рассчитанные в рамках С- модели индексом С.

В ΛCDM- модели, параметр (см., например, [6, 7]). Значение параметра в С-модели может быть значительно большим чем в ΛCDM- модели, так как в С-модели предполагается, что заметная часть «темной материи» может быть релятивисткой. Полагаем, что величины в ΛCDM- и С- моделях могут отличаться на два-три порядка.

При и формулы (6.1), (6.2) приближенно записываем в виде:

,	(6.4)
.	(6.5)

Из (6.3), (6.4) находим:

.

(6.6)

Эта формула определяет соотношение величин сил отталкивания и притяжения в процессе эволюции Вселенной в области в ΛCDM- модели. Видно, что в процессе эволюции отношение монотонно растет. За время от эпохи рекомбинации, когда , до современной эпохи, когда , величина (6.6) увеличилась приблизительно в миллиард раз. Вследствие существенного различия сил притяжения и отталкивания, согласно ΛCDM- модели, Вселенная расширяется неравномерно. Функция , описывающая расширение, являться сильно нелинейной.

Рис. 3. Характер зависимости космологических сил от радиуса кривизны. 1 – эйнштейновские силы отталкивания в ΛCDM- модели ( ); 2 – центробежные силы отталкивания в С-модели ( ); 3 – силы притяжения в ΛCDM- и С- моделях ( ).

В современной космологии считают, что отношение близко к трем(см. [6, 7, 17, 18]). При таком отношении величин параметров и , согласно ΛCDM- модели, силы отталкивания в современной Вселенной приблизительно в шесть раз больше, чем силы притяжения.

Соотношение сил отталкивания и притяжения в С- модели для времен, когда , согласно (6.4), (6.5), описывается формулой:

.

(6.7)

Параметр определяется формулой (5.28) и является универсальной постоянной С- модели. Его значения, вычисленное для любых моментов времени, является одном и тем же. Как видно из (6.7), параметр определяет величину отношения сил отталкивания и притяжения в С- модели в эпоху преобладания вклада нерелятивистской компоненты в полную массу космической среды.

Непосредственно использовать формулу (5.28) для определения значения не представляется возможным. В эту формулу входят плотности и , точность определения которых оставляет желать лучшего и, что существенно, она содержит радиус кривизны современной Вселенной непосредственное определение которого затруднительно. Выбор значения параметра аналогичен выбору значения космологической постоянной Λ в ΛCDM- модели. Параметр должен быть взят таким, чтобы С- модель правильно описывала наблюдения.

Теоретически, значение параметра может быть меньшим, равным или большим единицы. Если предположить, что значение параметра меньше единицы, то это, согласно С- модели, означает, что Вселенная во все времена расширяется с замедлением. Возможно, что это предположение является правильным, но оно находится в противоречии с выводами многочисленных работ последнего десятилетия (см., например, [3, 4, 6, 7, 16-20]) в которых доказывается, что расширение Вселенной происходит с ускорением.

Вывод об ускоренном расширении Вселенной, по-видимому, не является окончательно доказанным. Он сделан в рамках ΛCDM- модели, бесспорность которой не является очевидной. Безусловно, вариант ускоренного расширения Вселенной возможен. В то же время полагаем, что вариант ее расширения с замедлением пока также не является исключенным. В настоящей работе допускаем возможность обоих вариантов.

Из (5.25) видно, что равновесие сил притяжения и отталкивания достигается при , если:

.

(6.8)

Если , то равновесие сил наступило при . Если , то равновесие наступит при . Если же , то Вселенная, согласно С- модели, при всех расширяется с замедлением.

Значение , при котором силы отталкивания и притяжения в С-модели становятся равными по величине, обозначим как . Как видно из (5.25), находится из уравнения:

.

(6.9)

В современной космологии предполагается, что существующие структуры во Вселенной: галактики и их скопления, могли образоваться лишь в то время, когда определяющую роль играли силы притяжения. Считается, что существовал длительный период, благоприятный для роста этих структур. Предполагается, что процесс их формирования интенсивно происходил еще при [1, 7]. Если считать, что в это время силы гравитации были больше, чем силы отталкивания, то это автоматически означает, что . В С-модели значения параметров , и являются функциями независимых параметров и (см. пункт 6.3). Как будет показано в §8, согласно С-модели, .

Уравнение, определяющее значение , при котором согласно ΛCDM-модели имеет место переход от режима замедленного расширения к режиму ускоренного расширения, может быть записан в виде:

.

(6.10)

В ΛCDM-модели , поэтому из (6.10) следует: .
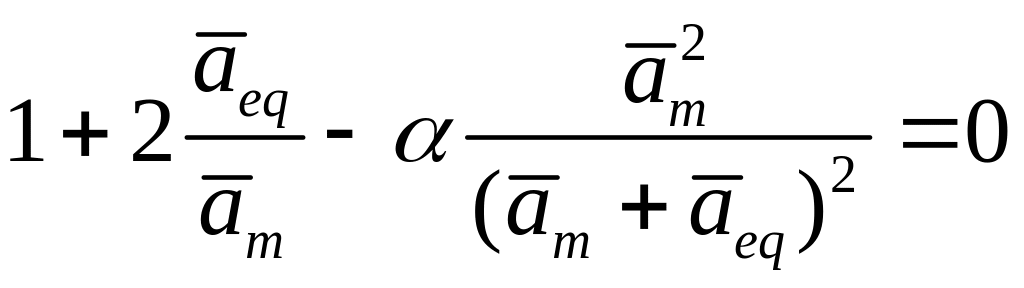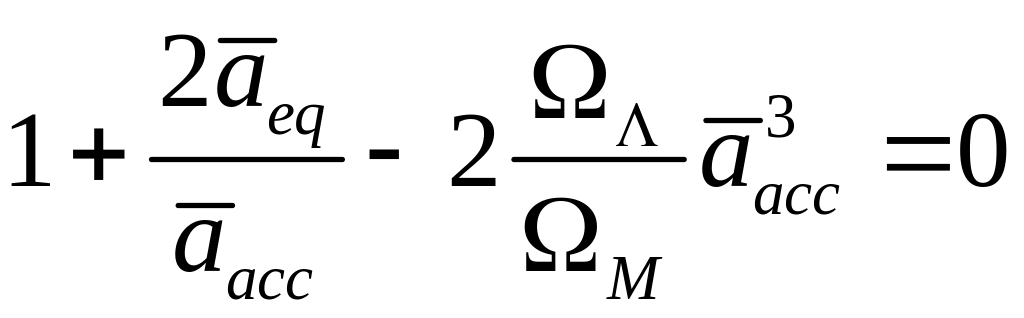