19. Соотношения неопределенности. Роль обратного флуктуационного влияния прибора. Стандартные квантовые пределы. Квантовые невозмущающие измерения. Квантовые эталоны единиц физических величин (примеры). Эффект Джозефсона и сверхпроводящие квантовые интерферометры.

Опыты Планка  Энергия фотона E = ħω

Опыты Лебедева по измерению давления света  Импульс фотона P = ħω/c

Если фотон монохроматичен, то есть описывается одной волной с фиксированной частотой, то он бесконечен по времени. Чтобы фотон был локализован во времени, нужно, чтобы он представлял собой сумму волн и имел конечную ширину спектра Δω. Δωτ ≥ 1.

Из неопределённости частоты следует неопределённость энергии

Чем хуже локализован фотон, тем лучше определена его энергия.

Длину фотона можно измерить по схеме Д. Колышко: фотон делится на два нелинейным кристаллом. Один фотон всегда падает не детектор, который включает оптический затвор, через который проходит второй фотон. Затвор можно двигать, измеряя тем самым корреляционную функцию между двумя фотонами, полученными из одного фотона.

Длина обычно определяется длиной кристалла и составляет Исходная когерентность лазера уменьшается из-за конечности длины фотона. Очень малые энергии можно измерять с помощью калориметров.

Соотношение неопределённостей импульс – координата:

Это соотношение неопределённости относится к фотону как к частице.

Микроскоп Гейзенберга

Микроскоп Гейзенберга – мысленный опыт по измерению координат тела, с помощью рассеяния на нём частиц. Схем может быть много.

Дифракция на щели. Характерный угол дифракции света θ = λ/d. Если фотоны летят по одному, то этот угол будет определять неопределённость положения отдельных фотонов.

Неопределённость поперечной координаты в случае пролёта через щель при этом соответствует ширине щели, т.е. d.

Таким образом, соотношение неопределённостей справедливо и для поперечных координат. Δp_⊥Δx_⊥ ~ħ.

Пусть мы пытаемся измерить координату щели по распределению измеренных фотонов. Для одного фотона Δx_щели ~ d. В случае большого числа фотонов Δx_щели ~ d/√N.

Поскольку при пролете через щель фотоны получают поперечный импульс, щель тоже должна получать импульс от фотонов и после измерения щель будет иметь неопределённость импульса: =

Тут опять же сохраняется соотношение неопределённости, но связано оно не с измерением, а с возмущением.

Квантовый измеритель скорости Фон Неймана

Фотон отражается от движущегося тела и изменяет свою скорость за счёт эффекта Доплера.

Ошибка измерения скорости за счёт неопределённости энергии фотона:

Отражаясь от тела фотон передаёт ему импульс в момент времени с неопределённостью τ. Длина фотона при этом тоже τ. Поэтому пробное тело в процессе измерения неконтролируемым образом сдвигается на координату:

Ошибка измерения скорости (импульса) и возмущение координаты связаны соотношением неопределённостей:

В результате квантовых измерений происходит измерение одной наблюдаемой величины и возмущение другой.

В квантовом измерении всегда есть необратимый процесс, связанный с квантовой считывающей системой: носители информации разрушаются при считывании.

Стандартный квантовый предел

Хотим измерить разность координат X = x₂ – x₁. Измерения проводятся с помощью квантового прибора типа микроскопа Гейзенберга.

Пусть ошибка первого измерения Δx₁, при этом в результате обратного влияния прибора объекту будет передан случайный импульс Δp₁. Этот импульс проявится во время второго измерения в виде добавочного возмущения координаты.

Δx_add = Δp₁τ/m = ħ τ/(2mΔx₁).

Ошибка измерения разности:

Ошибка разности координат ограничена снизу. Её нельзя свести в ноль.

Нижняя граница – стандартный квантовый предел.

Если мы измеряем изменение импульса через изменение координаты, то можно получить СКП для импульса:

Если изменение импульса вызвано силой, то СКП для силы равно:

СКП для гармонического осциллятора.

Измеряем координату в начале движения и через четверть периода, то есть в момент времени

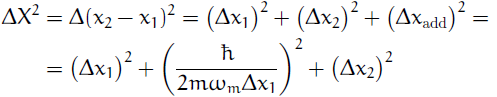
Для частоты 10³ с^-1 и массы 10 г, СКП ~ 10^-16 см.

Для импульса:

СКП для энергии

С какой ошибкой можно измерить изменение энергии механического осциллятора по измерению его координаты дважды в момент времени t = 0 и через четверть периода (как и в прошлый раз).

(кажется, тут должен быть «-»)

N – среднее число квантов в осцилляторе.

СКП для LC контура

ω_e – собственная частота LC-контура.

Схема с тремя измерениями

Схема с тремя измерениями избавляет от необходимости узнавать начальные условия (начальная координата и начальный импульс) или готовить систему так, чтобы начальные условия были заданными.