28. Фурье-анализ. Дискретное преобразование Фурье. Быстрое преобразование Фурье. Вэйвлетный анализ.

Дискретное преобразование Фурье

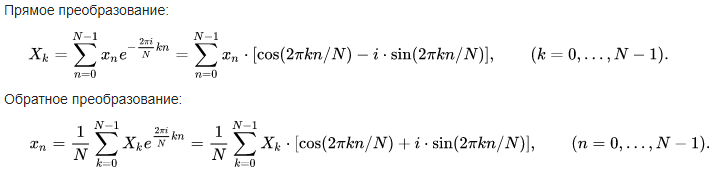
Матричное представление:

Теорема Котельникова

Любую функцию F(t) состоящую из частот от 0 до f₁ можно непрерывно передавать с любой точностью при помощи чисел, следующих друг за другом через 1/2f₁ секунд.

Быстрое преобразование Фурье

Прямое преобразование – это умножение матриц (см. выше).

N – количество точек. За счёт 2π периодичности:

i – любое целое.

Основная фишка: в формуле выше выражения X_k и X_{N/2 + k} отличаются только экспоненциальным множителем перед второй суммы. Остальное отличие в k съедается за счёт N/2 периодичности.

Далее по рекурсии.

Подробнее см. код примера тут: https://habr.com/ru/company/otus/blog/449996/

Вэйвлетный анализ

Если коротко, то это Фурье с временным разрешением. Основная идея: в отличии от синуса в вейвлете носитель конечен во времени.

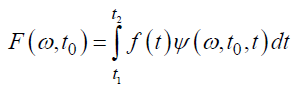
Морле использовал ядро

Это Фурье с оконной функцией.

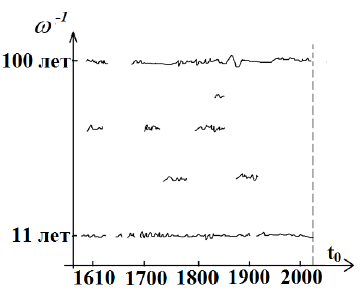
Ядро Морле не позволяет сделать обратное преобразование.

Чтобы была возможность сделать обратное преобразование, нужно, чтобы выполнялось условие:

Поэтому используют «Мексиканскую шляпу»:

Вид обратного преобразования достаточно сложный:

Обратное преобразование используется редко. Но иногда бывает полезно пофильтровать что-то с временным разрешением, а затем посмотреть, что из этого получится.

Источники

Вятчанин. Конспект лекций по курсу "Радиофизика"

https://habr.com/ru/company/otus/blog/449996/

Тихонов Н.А., Токмачев М.Г. Курс лекций «Основы Математического Моделирования»