16. Фундаментальные шумы в измерительных устройствах

Броуновское движение

Броуновское движение может вызывать колебания различных элементов измерительных приборов, что в свою очередь приводит к колебаниям показаний таких приборов. Пример: зеркальный гальванометр.

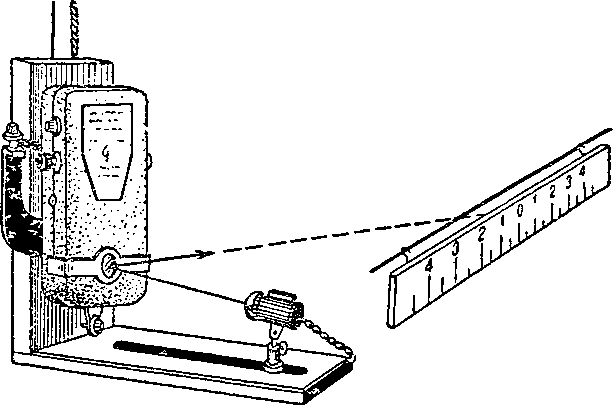
Зеркальный гальванометр позволяет очень точно измерить ток, поскольку его шкала вынесена далеко и за счёт этого может регистрировать очень малые отклонения луча. Молекулы воздух могут биться о зеркало и вызывать его колебания. Но усреднённый момент этих колебаний равен нулю.

Степень свободы одна, поэтому в случае термодинамического равновесия E_пот = Jφ²/2 = kT/2. <φ²/> = kT/J. Поэтому с достоверной точностью можно фиксировать только изменения тока, превышающие по величине тепловые колебания зеркала. Аналогичные оценки можно получить и для других электромеханических устройств: микрофонов, пьезоэлектрических преобразователей и т.д.

Тепловой шум

Неупорядоченное тепловое движение атомных частиц вызывает тепловой шум во всех электрических проводниках. Эквивалентная схема реального сопротивления: идеальный резистор + генератор шумового напряжения:

Рассмотрим пару длинных проводников, к которым присоединены два резистора, находящиеся в тепловом равновесии:

Шум можно рассматривать в спектральном представлении:

Волны, излучаемые одним резистором, движутся к другому резистору со скоростью v=ω/β и полностью там поглощаются. Каждый из резисторов является чем-то типа абсолютно чёрного тела. Общая энергия в диапазоне Δω равна:

E_ω Δω = 2P _ω Δω L/v.

Условия стоячей волны: nλ/2 = L. Чисто стоячих волн в Δω: Δn = LΔω/πv.

Среднее число фотонов (???) подчиняется распределению Бозе-Эйнштейна:

<N> = 1 / (e^ħω/kT - 1)

Таким образом, энергия в интервале частот Δω равна:

E_ω Δω = Δnħω/(e^ħω/kT - 1)

Мощность: P_ω= ħω/(e^ħω/kT - 1) не зависит от сопротивления.

Если ħω << kT, то мощность шумов не зависит от частоты – белый шум.

При ħω >> kT мощность шумов мала мала. При комнатной температуре переход соответствует примерно 600 ГГц – длина волны ~ 1 мм.

I = U / 2R.

Мощность на одном из проводников: I²R = U²/4R = P Δω.

U² = 4kTR Δω (ħω/kT)/(e^ħω/kT - 1) – Формула Найквиста.

При малых частотах W(ω) = U²/ Δω = 4kTR.

Пример: R = 2 Мом, полоса частот 100 МГц, эффективное напряжение шума на этом сопротивлении будет 2,6 мВ.

Дробовой шум

Дробовой шум связан с дискретностью протекающих по проводнику зарядов. Рассмотрим пример для вакуумного диода. Электроны вылетают из нагретого катода, имя пренебрежимо малую скорость. Считаем, что поле однородное и ускорение электронов в поле между электродами однородно:

Продолжительность импульса тока τ равна времени пролёта электрона от катода к аноду.

Ток можно разложить на постоянный и шумовой:

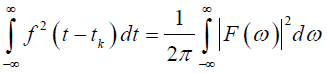
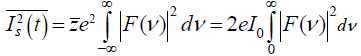
z – частот пролетания электронов.

Частотная зависимость определяется только формой импульсов тока. При низких частотах импульсов:

Таким образом, шумовой ток не зависит от частоты.

Для тока I₀ = 2 мА и полосы частот 2 кГц Is эфф. = 2,4 нА.

Фликкер-шум

Изначально наблюдался в электронных лампах с оксидными катодами. Обуславливался тем, что в таких катодах флуктуирует работа выхода электронов. Эти флуктуации вызывают флуктуации тока. Существует достаточно большой класс устройств (в том числе полупроводниковых) с флуктуирующей работой выхода. Этот шум заметен в основном в области низких частот. Мощность изменяется примерно как 1/f.

Генерационно-рекомбинационный шум

В полупроводниковых устройствах может возникать специфический аналог дробового шума. Основное отличие полупроводников от вакуумного диода заключается в том, что среднее время жизни носителей заряда в полупроводниках мало по сравнению с временем, необходимым для переноса носителя через всю рабочую область.

I ~ I²/(1 + f²/f_g²) Δf

Ниже пороговой частоты мощность не зависит от частоты (белый шум), а выше – убывает, как 1/f². Пороговая частота зависит от среднего времени жизни носителя заряда. Аналогичная спектральная зависимость получится, если пропустить белый шум через RC-цепь.

Квантовый шум

Обусловлен квантовой природой электромагнитного поля. Пусть имеется детектор с квантовым выходом 1 (каждый фотон рождает по одному электрону). Импульсы ЭМ поля преобразуются в импульсы тока. Таким образом, мы можем регистрировать флуктуации поля.

Пусть на детектор падает монохроматическое излучение (флуктуаций быть не должно). Тогда:

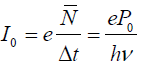
Но наблюдаемое число фотонов флуктуирует в соответствии с распределением Пуассона.

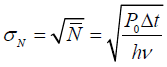
2 – от того, что тут мы рассматриваем только положительные Δν, а отклонения от основной линии могут быть как в положительную, так и в отрицательную сторону.

Если нет внутренних шумов, то .

В случае гетеродинирования или других преобразования частот шумы будут умножаться. Квантовый шум линейно растёт с частотой. В областях hω >> kT он начинает преобладать над тепловым.

В случае некогерентных источников (например, лампы накаливания) квантовые шумы возрастают по сравнению со случаем монохроматического излучения.

Источники

В. Н. Романов. Фундаментальные шумы в измерительных устройствах.