26. Техника оценки параметров при разных распределениях погрешностей измерений. Средние и вероятные значения переменных. Техника оценки параметров при асимметричных распределениях погрешностей. Суммирование результатов различных измерений. Робастные оценки. Параметрические и непараметрические оценки.

Лекции Воронцова.

http://www.machinelearning.ru/wiki/index.php?title=Робастное_оценивание

Техника оценки параметров при разных распределениях погрешностей измерений

Для каждого измерения вводятся весовые коэффициенты, которые отражают надёжность данного измерения.

Пример – МНК с весами.

Если мы знаем погрешности – всё хорошо. Если нет – нужно как-то по результатам измерений оценивать надёжность каждой конкретной точки.

Можно делать динамические коэффициенты, которые будут строиться на основе того, как далеко текущее значение от модели (например, от среднего в случае усреднения).

Средние и вероятные значения переменных

Среднее и наиболее вероятное – не всегда одно и то же.

Наиболее вероятная скорость:

Средняя скорость:

Техника оценки параметров при асимметричных распределениях погрешностей

То есть задача заключается в том, чтобы подобрать параметр θ таким образом, чтобы функция правдоподобия была максимальной (один из вариантов), т.е. чтобы полученные результаты измерений были наиболее вероятными.

Метод максимума правдоподобия

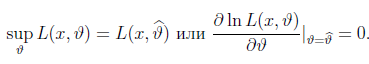
Где-то берут просто производную от функции, но, насколько я понимаю, логарифм удобнее. Поскольку логарифм –функция монотонная, проблем возникать не должно.

Можно доказать, что:

Робастные оценки

Робастность - нечувствительность к малым отклонениям от предположений. Общая идея – использование взвешенных выборок с динамическим подбором коэффициентов.

Параметрические оценки

Параметрические оценки – есть модель распределения и в ней есть неизвестные параметры. Задача заключается в том, чтобы найти эти неизвестные параметры по измеренной выборке.

Примеры – МНК (на эту тему есть отдельный билет).

Непараметрические оценки

Непараметрическая оценка – хотим построить распределения, не зная его модели (есть модель – есть параметры, нет модели – непонятно, что подбирать).

То есть мы просто вводим функцию, которая размажет нам ступеньки.