24. Оценка параметров случайных величин. Выборочные средние и дисперсии. Выборочные распределения. t-распределение Стьюдента, χ2-распределение.

Выборка объёма n – случайный вектор (ξ₁,…, ξ_n). Координаты вектора – элементы выборки – независимые случайные величины с одной и той же функцией распределения F(x).

Выборочная (эмпирическая) функция распределения (оценка функции распределения на основе результатов измерения):

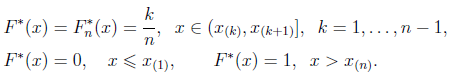
Ступеньки идут с равной высотой по y (k/n). При этом шаг по x определяется измеренными значениями x.

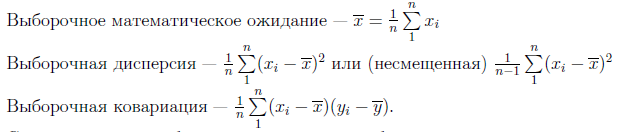
Смещённая дисперсия предполагает, что истинное значение <x> мы уже знаем. Несмещённая подразумевает, что мы его считаем также по полученной выборке.

Распределение χ2 (Пирсона)

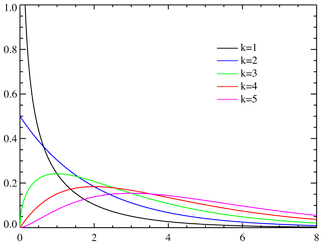
Распределение t (Стьюдента)

Распределение Стьюдента описывает отношение нормально распределённой случайной величины к величине, распределённой по хи-квадрат.

Альтернативное определение контролируемой величины:

Распределение Стьюдента используется для t-теста - проверки гипотезы о том, что величины из некоторой выборки имеют нормальное распределение:

Как это работает (предположение):

Рисуем распределение. Определяем область, где лежат 99% всех точек. Затем вычисляем значение t (одно число) и смотрим, куда оно попало. Если оно попало в нашу область, то, вероятно, всё хорошо (но это не точно). Если не попало – то всё почти наверняка очень плохо.

Источники

Лекции по математической статистики с cmp.phys.msu.ru

Худсон. Статистика для физиков

https://habr.com/ru/post/311092/#hi