19. Определение перемещения бруса случаем Верещагина.

П равило Верещагина – графоаналитич. прием вычисления интегралов. Заключается в замене операций интегрирования перемножением площади эпюры моментов от внешней нагрузки F на ординату у_с линейной эпюры моментов от единич. силы F₀, расположенную под центром тяжести площади первой эпюры. Исп.только если жесткость сечения бруса по всей длине постоянна, т.к. эпюры от единич. силовых факторов на прямолинейн. участках оказываются линейными: M_x1=f(z)=b+kz. Интеграл _(l)∫MxFMx1dz можно заменить на ₍₀₎∫^(l)f₁(z)f₂(z)dz=₍₀₎∫^(l)f₁(z)(b+kz)dz=b₍₀₎∫^(l)f₁(z)dz+k₍₀₎∫^(l)zf₁(z)dz. С – центр тяжести. Интеграл Мора, составленный для каж. из участков нагружения балки, = произведению площади F нелинейн. эпюры изгиб. моментов M_xF на ординату у_с эпюры изгиб. момента М_х1, соотв-щую положению центра тяжести площади F: Vk=∑F∙y_c/EIx.

20. Напряженное состояние в точках тела. Главные площадки и главные напряжения. Виды напряженного состояния.

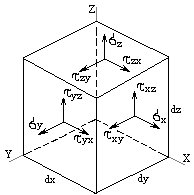
Напряженное состояние в точке тела – совокупность напряжений во мн-ве площадок, проходящих через заданную точку. Исследование напряженного состояния необходимо для расчета на прочность в сложном случае напряжения. Моделью служит куб, параллелепипед. σ_ij: i – перпендикулярная ось, j – вдоль. Из условия равновесия элементарного куба τ_yx=τ_xy. F=τ·S= τ_xy·(dz·dy)·dx; τ_yx=dx·dz·dy·τ_xy. => τ_yx=τ_xy.

Напряженное состояние элементарного куба описывается 9 компонентами (3 нормальных, 6 касательных). Учитывая закон парности касат.напряжений (τ_yx=τ_xy), напряженное состояние описывается 6 компанентами.

Понятие о главных напряжениях. Через заданную точку всегда можно провести только 3 взаимноперпендик. площадки, в которых τ=0. Это главные площадки, а нормальные напряжения – главные напряжения. Взаимные соотношения между главными напряжениями: σ₁≥σ₂≥σ₃.

Сущ. 3 вида напряженного состояния тела:

1 . действует только одно главное напряжение σ₁ – одноосное напряженное состояние (растяжение).

2. действуют σ₁, σ₂ – плоское напряженное состояние (двуосное).

3. объемное напряженное состояние (трехосное).

21=17. Деформация бруса при объемном напряженном состоянии. Обобщенный закон Гука.

22. Теории (гипотезы) прочности и их назначение. Понятие об эквивалентных напряжениях. Содержание и области применения теории прочности.

Предельное напряженное состояние у пластич. материалов возник. при остаточных деформациях, у хрупких – просто разрушение. Оценить прочность детали находящейся в сложном напряженном состоянии через хорошо известное простое напряженное состояние - растяжение – самое хорошо изученное. Эквив. напряжение – кот. необходимо создать в растянутом стержне, чтобы его напряженное состояние было эквивалентно сложнонапряженному состоянию, кот. рассматривается. Суть гипотез прочности: сложное выразить через простое. Т1: О наиб. σ, Галилей – Причина разрушения материала есть наиб. нормальное напряжение в к.-л. точке, в к.-л. направлении. Для тв. материалов; недостаток: не учитывает глав. напряжения σ₂ и σ₃. σ_max≤[σ]. Т2: О наиб. линейных деформациях, Мариотт – Прочность материала в данной точке завис. от величины деформации. ε_max≤[ε]. Из з-на Гука σ=Eε. Тогда σ₁/Е – μσ₂/Е – μσ₃/Е≤[σ]/Е, σ_экв=σ₁–μσ₂–μσ₃ ≤ [σ]. Т3: О наиб. τ, Кулон – Разрушение происх. когда в к.-л. точке на двух взаимноперпендик. площадках τ достигает предельного значения. Для пластич. материалов; недост: не учитывает глав. напряжение σ₂. τ_max≤[τ]. (σ₁-σ₃)/2 ≤ [σ]/2, σ_экв=σ₁-σ₃ ≤ [σ]. Для плоского напряженного состояния σ_экв=√(σ²+4τ²)≤ [σ]. Т4: Энергетическая теория, Бельтрами – Предельное напряженное состояние возник. при некотором значении потенциальной энергии, затрачиваемой на формообразование. Uф≤[Uф]. Для плоского напряженного состояния σ_экв=√(σ²+3τ²)≤ [σ]. Т5: Оскара Мора – Прочность материала завис. от вел-ны и знака наибольших и наим. глав. напряжений. σ₁–kσ₃≤[σ], где k – коэф., учитывающий различ. поведения материала при растяжении и сжатии. k=[σ_р]/ [σ_с], k=[σ_вр]/ [σ_вс].