Признак делимости на 5
Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5, т. е. если она 0 или 5.
Соответствующая признаку функция:
Эта функция помимо признака делимости задаёт и признак равноостаточности.
Признак делимости на 6
Число делится на 6 тогда и только тогда, когда оно делится и на 2, и на 3 (то есть если оно четное и сумма его цифр делится на 3).
Другой признак делимости: число делится на 6 тогда и только тогда, когда учетверённое число десятков, сложенное с числом единиц делится на 6.
Соответствующая признаку функция:
Эта
функция помимо признака делимости
задаёт и признак равноостаточности.
Например, числа 73, 
и 
равноостаточны
при делении на 6.
Признак делимости на 7
Признак
1:
число делится на 7 тогда
и только тогда, когда утроенное число
десятков, сложенное с числом единиц
делится на 7. Например, 154 делится на 7,
так как на 7 делится 
Другой
пример — число 1001 делится на 7, так
как на 7 делятся 
Соответствующая этому признаку функция:
Эта
функция помимо признака делимости
задаёт и признак равноостаточности.
Например, числа 87, 
и 
равноостаточны
при делении на 7.
Признак
2:
число делится на 7 тогда и только тогда,
когда разность числа десятков и удвоеного
числа единиц, взятая по модулю, делится
на 7. Например, 364 делится на 7, так как на
7 делится 
Соответствующая этому признаку функция:
Признак
3.
число делится на 7 тогда и только тогда,
когда модуль алгебраической суммы
чисел, образующих нечётные группы по
три цифры (начиная с единиц), взятых со
знаком «+», и чётных со знаком «-» делится
на 7. Например, 138689257 делится на 7, так как
на 7 делится 
Соответствующая этому признаку функция:
Признак делимости на 8
Число
делится на 8 тогда
и только тогда, когда число, образованное
тремя его последними цифрами, делится
на 8. Трёхзначное число делится на 8 тогда
и только тогда, когда число единиц,
сложенное с удвоеным числом десятков
и учетверённым числом сотен, делится
на 8. Например, 952 делится на 8 так как на
8 делится 
Соответствующая признаку функция:
Эта
функция помимо признака делимости
задаёт и признак равноостаточности.
Например, числа 567, 
и 
равноостаточны
при делении на 8.
Признак делимости на 9
Число
делится на 9 тогда
и только тогда, когда сумма его цифр
делится на 9. Например, 12345678 делится на
9, то есть на 9 делится 
Соответствующая признаку функция:
Эта
функция помимо признака делимости
задаёт и признак равноостаточности.
Например, числа 345, 
и 
равноостаточны
при делении на 9.
Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на 0.
Соответствующая этому признаку функция:
Эта функция помимо признака делимости задаёт и признак равноостаточности.
Признаки делимости на 11
Признак
1: число
делится на 11 тогда
и только тогда, когда модуль разности
между суммой цифр, занимающих нечётные
позиции, и суммой цифр, занимающих чётные
места делится на 11. Например, 9163627 делится
на 11, так как 
делится
на 11. Другой пример — 99077 делится на
11, так как 
делится
на 11.
Соответствующая этому признаку функция:
Признак
2: число
делится на 11 тогда и только тогда, когда
на 11 делится сумма чисел, образующих
группы по две цифры (начиная с единиц).
Например, 103785 делится на 11, так как на
11 делятся 
и 
Соответствующая признаку функция:
Эта
функция помимо признака делимости
задаёт и признак равноостаточности.
Например, числа 123456, 
и
равноостаточны
при делении на 11.
Признак делимости на 12
Число
делится на 12 тогда
и только тогда, когда модуль разности
числа единиц и удвоеного числа десятков
делится на 12. Например: 1236 делится на
12, так как 
делится
на 12.
Соответствующая этому признаку функция:
Признак делимости на 13
Число
делится на 13 тогда
и только тогда, когда сумма числа десятков
с учетверенным числом единиц делится
на 13. Например 845 делится 13, так как на
13 делятся 
и 
Соответствующая этому признаку функция:
Признак делимости на 17
Число
делится на 17 тогда
и только тогда, когда модуль разности
числа десятков и пятикратного числа
единиц делится на 17. Например, 221 делится
на 17, так как 
делится
на 17.
Соответствующая этому признаку функция:
Признак делимости на 19
Число
делится на 19 тогда
и только тогда, когда число десятков,
сложенное с удвоенным числом единиц,
делится на 19. Например, 646 делится на 19,
так как на 19 делятся 
и 
Соответствующая этому признаку функция:
Признак делимости на 20
Число делится на 20 тогда и только тогда, когда число, образованое двумя последними цифрами, делится на 20.
Соответствующая этому признаку функция:
Эта функция помимо признака делимости задаёт и признак равноостаточности.
Признаки делимости на 23
Признак
1:
число делится на 23 тогда
и только тогда, когда число сотен,
сложенное с утроенным числом, образованым
двумя последними цифрами, делится на
23. Например, 28842 делится на 23, так как на
23 делятся 
и 
Соответствующая этому признаку функция:
Признак
2:
число делится на 23 тогда
и только тогда, когда число десятков,
сложенное с семикратным числом единиц,
делится на 23. Например, 391 делится на 23,
так как 
делится
на 23.
Соответствующая этому признаку функция:
Признак
3:
число делится на 23 тогда
и только тогда, когда число сотен,
сложенное с семикратным числом десятков
и утроенным числом единиц, делится на
23. Например, 391 делится на 23, так
как 
делится
на 23.
Соответствующая этому признаку функция:
Признак делимости на 25
Число делится на 25 тогда и только тогда, когда число, образованое двумя последними цифрами, делится на 25.
Соответствующая этому признаку функция:
Эта функция помимо признака делимости задаёт и признак равноостаточности.
Признак делимости на 27
Число делится на 27 тогда и только тогда, когда на 27 делится сумма чисел, образующих группы по три цифры (начиная с единиц).
Соответствующая признаку функция:
Эта функция помимо признака делимости задаёт и признак равноостаточности.
Признак делимость на 29
Число
делится на 29 тогда
и только тогда, когда число десятков,
сложенное с утроенным числом единиц,
делится на 29. Например, 261 делится на 29,
так как 
делится
на 29.
Соответствующая этому признаку функция:
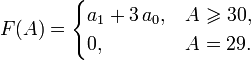
Признак делимости на 30
Число делится на 30 тогда и только тогда, когда оно заканчивается на 0 и сумма всех цифр делится на 3.
Признак делимости на 31
Число
делится на 31 тогда
и только тогда, когда модуль разности
числа десятков и утроенного числа единиц
делится на 31. Например, 217 делится на 31,
так как 
делится
на 31.
Соответствующая этому признаку функция:
Признак делимости на 37
Признак 1: число делится на 37 тогда и только тогда, когда на 37 делится сумма чисел, образующих группы по три цифры (начиная с единиц).
Соответствующая признаку функция:
Эта функция помимо признака делимости задаёт и признак равноостаточности.
Признак
2: число
делится на 37 тогда и только тогда, когда
на 37 делится модуль утроеного числа
сотен, сложенного с учетверённым числом
десятков, за вычетом числа единиц,
умноженного на семь. Например, число
481 делится на 37, так как на 37 делится 
Признак
3: число
делится на 37 тогда и только тогда, когда
на 37 делится модуль суммы числа сотен
с числом единиц, умноженного на десять,
за вычетом числа десятков, умноженного
на 11. Например, число 481 делится на 37, так
как на 37 делится 
Соответствующая признаку функция:
