
- •Предмет физики и ее связь с другими науками. Единицы физических величин. Система си. Предмет физики и ее связь с другими науками.
- •Единицы физических величин.
- •Кинематика и динамика. Основные физические модели: материальная точка, система частиц, абсолютно твердое тело, сплошная среда.
- •Пространственно-временные отношения. Относительность движения. Система отсчета.
- •Кинематическое описание движения. Перемещение, скорость, ускорение.
- •Кинематика движения по криволинейной траектории. Тангенциальная и нормальная составляющие ускорения.
- •Движение по окружности. Угловая скорость и угловое ускорение.
- •Связь между угловыми и линейными характеристиками движения.
- •Основная задача динамики. Масса, импульс, сила. Законы Ньютона.
- •Силы в природе. Силы трения.
- •Понятие замкнутой системы. Закон сохранения и изменения импульса.
- •Центр масс.
- •Реактивное движение. Уравнение Мещерского.
- •Теория удара. Абсолютно упругий и абсолютно неупругий удары.
- •Работа. Мощность.
- •Кинетическая энергия.
- •Консервативные и диссипативные силы. Потенциальная энергия.
- •Закон сохранения и изменения энергии в механике.
- •Законы сохранения и симметрия пространства и времени.
- •Движение твердого тела. Момент инерции. Момент инерции твердых тел разной формы.
- •Теорема Штейнера.
- •Кинетическая энергия твердого тела, совершающего поступательное и вращательное движение.
- •Момент силы. Уравнение движения твердого тела, вращающегося вокруг неподвижной оси. Момент импульса.
- •Закон сохранения и изменения момента импульса.
- •Деформации твердого тела.
- •Описание движения в неинерциальных системах отсчета. Силы инерции.
- •Вязкость. Ламинарное и турбулентное течение. Число Рейнольдса.
- •Принцип относительности Галилея. Преобразования Галилея. Инварианты преобразования.
- •Постулаты специальной теории относительности. Преобразования Лоренца.
- •Основной закон релятивистской динамики материальной точки. Закон взаимосвязи массы и энергии. Основной закон релятивистской динамики материальной точки.
- •Закон взаимосвязи массы и энергии
- •Гармонические колебания и их характеристики. Амплитуда, частота и фаза гармонических колебаний.
- •Скорость, ускорение гармонических колебаний.
- •Гармонический осциллятор. Пружинный, физический и математический маятники.
- •Движение гармонического осциллятора при наличии сил сопротивления. Свободные затухающие колебания.
- •Вынужденные механические колебания. Явление резонанса.
Движение по окружности. Угловая скорость и угловое ускорение.
Движение
тела по окружности
является частным случаем криволинейного
движения. Наряду с вектором перемещения
![]() удобно
рассматривать угловое
перемещение
Δφ (или угол
поворота),
измеряемое в радианах
(рис. 1.6.1). Длина дуги связана с углом
поворота соотношением
удобно
рассматривать угловое
перемещение
Δφ (или угол
поворота),
измеряемое в радианах
(рис. 1.6.1). Длина дуги связана с углом
поворота соотношением
Δl = RΔφ. |
При малых углах поворота Δl ≈ Δs.
|
Рисунок
1.6.1. Линейное
и
угловое
|
Угловой скоростью ω тел в данной точке круговой траектории называют предел (при Δt → 0) отношения малого углового перемещения Δφ к малому промежутку времени Δt:
|
Угловая скорость измеряется в рад/с. Связь между модулем линейной скорости υ и угловой скоростью ω:
υ = ωR. |
При
равномерном движении тела по окружности
величины υ и ω остаются неизменными. В
этом случае при движении изменяется
только направление вектора
![]() Равномерное
движение тела по окружности является
движением с ускорением. Ускорение
Равномерное
движение тела по окружности является
движением с ускорением. Ускорение
|
направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями:
|
Для
доказательства этого выражения рассмотрим
изменение вектора скорости
![]() за
малый промежуток времени Δt. По определению
ускорения
за
малый промежуток времени Δt. По определению
ускорения
|
Векторы
скоростей
![]() и
и
![]() в
точках A и B направлены по касательным
к окружности в этих точках. Модули
скоростей одинаковы υA = υB = υ. Из подобия
треугольников OAB и BCD (рис. 1.6.2) следует:
в
точках A и B направлены по касательным
к окружности в этих точках. Модули
скоростей одинаковы υA = υB = υ. Из подобия
треугольников OAB и BCD (рис. 1.6.2) следует:
|
|
Рисунок
1.6.2. Центростремительное ускорение
тела
|
При малых значениях угла Δφ = ωΔt расстояние |AB| =Δs ≈ υΔt. Так как |OA| = R и |CD| = Δυ, из подобия треугольников на рис. 1.6.2 получаем:
|
При малых углах Δφ направление вектора приближается к направлению на центр окружности. Следовательно, переходя к пределу при Δt → 0, получим:
|
При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным. В векторной форме центростремительное ускорение может быть записано в виде
|
где
![]() –
радиус-вектор точки на окружности,
начало которого находится в ее центре.
Если тело движется по окружности
неравномерно, то появляется также
касательная
(или тангенциальная)
составляющая ускорения.
–
радиус-вектор точки на окружности,
начало которого находится в ее центре.
Если тело движется по окружности
неравномерно, то появляется также
касательная
(или тангенциальная)
составляющая ускорения.
|
В
этой формуле Δυτ = υ2 – υ1 – изменение
модуля скорости за промежуток времени
Δt. Направление вектора полного ускорения
![]() определяется
в каждой точке круговой траектории
величинами нормального и касательного
ускорений (рис. 1.6.3).
определяется
в каждой точке круговой траектории
величинами нормального и касательного
ускорений (рис. 1.6.3).
|
Рисунок
1.6.3. Составляющие ускорения
и
|
Движение тела по окружности можно описывать с помощью двух координат x и y (плоское движение). Скорость тела в каждый момент можно разложить на две составляющие υx и υy (рис. 1.6.4). При равномерном вращении тела величины x, y, υx, υy будут периодически изменяться во времени по гармоническому закону с периодом
|
|
Рисунок
1.6.4. Разложение вектора скорости
|
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
![]()
Вектор
![]() направлен вдоль оси вращения по
правилу правого винта, т.е. так же, как
и вектор
направлен вдоль оси вращения по
правилу правого винта, т.е. так же, как
и вектор
![]() (рис.7). Размерность угловой скорости
dim =T–1,
а ее единица — радиан в секунду
(рад/с).
(рис.7). Размерность угловой скорости
dim =T–1,
а ее единица — радиан в секунду
(рад/с).
Линейная скорость точки (см. рис. 6)
![]()
т. е.
![]()

В векторном виде формулу для линейной скорости можно написать как векторное произведение:
![]()
При этом модуль векторного произведения,
по определению, равен
![]() ,
а направление совпадает с направлением
поступательного движения правого винта
при его вращении от
к R.
,
а направление совпадает с направлением
поступательного движения правого винта
при его вращении от
к R.
Если (![]() = const, то вращение равномерное
и его можно характеризовать периодом
вращения T —
временем, за которое точка совершает
один полный оборот, т.е. поворачивается
на угол 2. Так как
промежутку времени t
= T соответствует
= const, то вращение равномерное
и его можно характеризовать периодом
вращения T —
временем, за которое точка совершает
один полный оборот, т.е. поворачивается
на угол 2. Так как
промежутку времени t
= T соответствует
![]() = 2,
то
= 2/T,
откуда
= 2,
то
= 2/T,
откуда
![]()
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:
![]()
откуда
![]()
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
![]()
При вращении тела вокруг неподвижной
оси вектор углового ускорения направлен
вдоль оси вращения в сторону вектора
элементарного приращения угловой
скорости. При ускоренном движении вектор
![]() сонаправлен вектору
(рис.8), при замедленном — противонаправлен
ему (рис.9).
сонаправлен вектору
(рис.8), при замедленном — противонаправлен
ему (рис.9).
Тангенциальная составляющая ускорения![]()
![]()
Нормальная составляющая ускорения
![]()


 1
1 2
2 3
3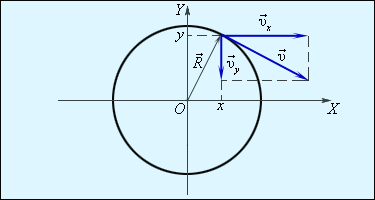 4
4