34. Движение гармонического осциллятора при наличии сил сопротивления. Свободные затухающие колебания.

35. Вынужденные механические колебания. Явление резонанса.

 Рассмотрим систему, на которую, кроме упругой силы (– kx) и сил сопротивления (– rυ), действует добавочная периодическая сила F –вынуждающая сила. Для колебаний вдоль оси x запишем:

      – основное уравнение колебательного процесса, или

(3.3.1)

      где f_x = F_x/m – вынуждающая сила, изменяющаяся по гармоническому закону:

      Через некоторое время после начала действия вынуждающей силы колебания  системы  будут  совершаться  с  частотой  вынуждающей  силы ω.

       Уравнение установившихся вынужденных колебаний:

(3.3.2)

      Наша задача найти амплитуду А и разность фаз φ между смещением вынужденных колебаний и вынуждающей силой.

      Обратим внимание на то, что скорость на π/2 опережает смещение, а ускорение на π/2 опережает скорость (см. п. 1.3).

      Из (3.3.2) получим:

(3.3.3)

(3.3.4)

      Преобразуем и (3.3.2) через косинус:

(3.3.5)

      Обозначим    – угол между смещением и вынуждающей силой.

      Подставим (3.3.3), (3.3.4) и (3.3.5) в (3.3.1):

 

      Каждое слагаемое последнего уравнения можно представить в виде соответствующего вращающегося вектора амплитуды:

          – амплитуда ускорения;    – амплитуда скорости;    – амплитуда смещения;    – амплитуда вынуждающей силы, причем 

               Вектор амплитуды силы найдем по правилу сложения векторов:

 .

Рис. 3.3

      Из рис. 3.2  видно, что   . Найдем амплитуду А:

(3.3.7)

      Таким образом,    и   .

      При постоянных F₀, m и β  амплитуда зависит только от соотношения круговых частот вынуждающей силы ω и свободных незатухающих колебаний системы ω₀.

      Начальную фазу вынужденных колебаний можно найти из выражения

(3.3.8)

      Из рис. 3.3 видно, что сила опережает смещение на угол, который определяется из выражения

 .

      Проанализируем выражение (3.3.7).

      1)    (частота вынуждающей силы равна нулю), тогда

      – статическая амплитуда (колебания не совершаются).

      2)    (затухания нет). С увеличением ω (но при   ) амплитуда растет и при   резко возрастает (   ). Это явление называется резонанс. При дальнейшем увеличении ω (   ) амплитуда опять уменьшается (рис. 3.4).

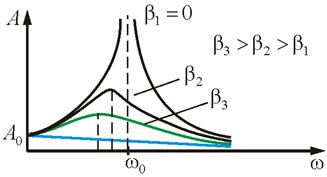
Рис. 3.4

      3)    Амплитуда будет максимальна при минимальном значении знаменателя. Для нахождения точки перегиба возьмем первую производную по ω от подкоренного выражения (3.3.7) и приравняем ее к нулю:

      4) ω ≠ 0, следовательно, выражение в скобках равно нулю:

 , отсюда

      где ω_рез – резонансная частота.

      Явление возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к ω_рез называетсярезонансом.

      Для консервативной системы, т.е.    из (3.3.9) следует   ; для диссипативной ω_рез несколько меньше собственной круговой частоты ω₀ (рис. 3.4).

      С увеличением коэффициента затухания β явление резонанса проявляется все слабее и исчезает при   .