
- •Министерство образования и науки республики казахстан
- •Учебная программа дисциплины – Syllabus
- •Данные о дисциплине:
- •1.5 Описание дисциплины
- •1.6 Контроль и оценка знаний.
- •Оценка знаний студентов
- •Содержание Активного раздаточного материала
- •Тематический план курса
- •2.2. Конспект лекционных занятий
- •Ранг матрицы
- •Определение. Системой из m линейных алгебраических уравнений с n неизвестными называется система вида:
- •Векторы и линейные операции над ними. Скалярное и векторное произведения. Смешанное произведение трех векторов.
- •Первый замечательный предел
- •Второй замечательный предел
- •1. Дифференцирование сложной функции
- •Асимптоты графика функции
- •1. Замена переменной в неопределенном интеграле.
- •2. Метод подведения под знак дифференциала
- •3. Метод интегрирования по частям
- •4. Интегрирование рациональных функций
- •4.1. Интегрирование функций, содержащих квадратный трехчлен.
- •4.2. Интегрирование рациональных функций
- •5. Интегрирование некоторых тригонометрических функций
- •Определение определенного интеграла
- •Дифференциальные уравнения первого порядка
- •Задача Коши. Теорема существования и единственности
- •Рассмотрим дифференциальное уравнение вида , где правая часть есть произведение функции, зависящей только от , на функцию, зависящую только от .
- •2.3 Планы практических занятий
- •Практическое занятие № 9. Исследование поведения функций и их графиков. Приложения дифференциального исчисления к геометрии.
- •Планы занятий в рамках самостоятельной работы студентов (срс)
- •2.7. Варианты тестовых заданий для самоконтроля
- •2.9 Экзаменационные вопросы по курсу
Первый замечательный предел
![]() .
.
Второй замечательный предел
![]() .
.
Непрерывность функции
Определение.
Функция
называется непрерывной в
точке
![]() ,
если выполняются три условия:
,
если выполняются три условия:
существует
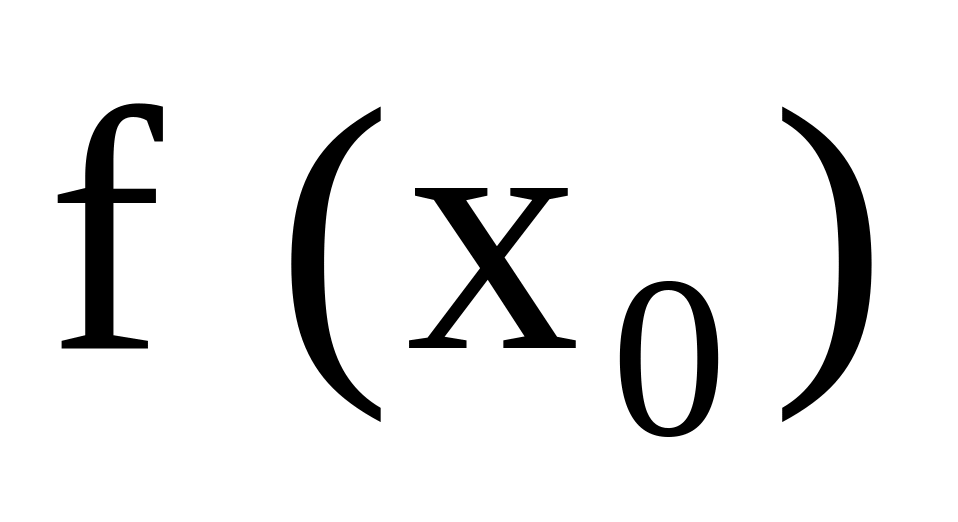 ;
;существует
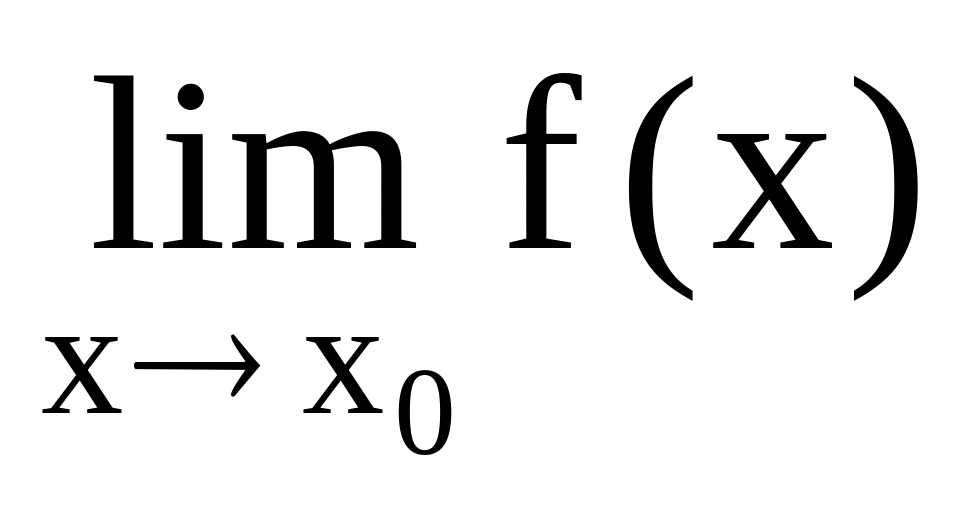 ;
;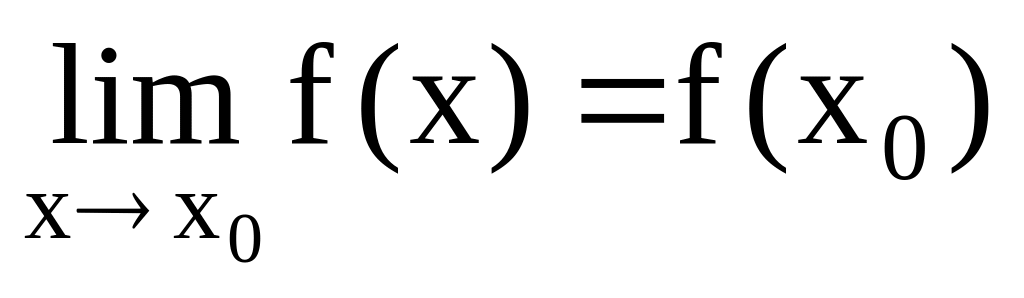 .
.
В символической форме это определение записывается так:
![]() .
.
Теорема (о
непрерывности монотонной функции).
Пусть функция
монотонна (монотонно возрастает или
монотонно убывает) на отрезке а,
![]()
и принимает все значения из отрезка
и принимает все значения из отрезка
![]() ,
тогда она непрерывна в каждой точке
интервала (а,
),
непрерывна в точке а справа и в
точке
,
тогда она непрерывна в каждой точке
интервала (а,
),
непрерывна в точке а справа и в
точке
![]() слева.
слева.
Из этой теоремы следует, что все основные элементарные функции непрерывны во всех внутренних точках своей области определения, а во всех граничных точках области определения, принадлежащих ей, они непрерывны справа и слева. Это следует из того, что
любую точку из области определения основной элементарной функции можно включить в отрезок, где эта функция монотонна и принимает все значения из отрезка
![]() .
.
Например, функция
![]() непрерывна во всех точках интервала
(–1,1), непрерывна в точке
непрерывна во всех точках интервала
(–1,1), непрерывна в точке
![]() справа и в точке
справа и в точке
![]() слева, так как оно монотонно возрастает
в
слева, так как оно монотонно возрастает
в
![]() и для
и для
![]() .
.
Теорема Пусть
функции
![]() и
и
![]() непрерывны
в точке
непрерывны
в точке
![]() .
Тогда функции
.
Тогда функции
1)
![]() ,
2)
,
2)
![]() ,
3) при
,
3) при
![]() .
Также непрерывны в точке
.
.
Также непрерывны в точке
.
Теорема
(непрерывность сложной функции).
Пусть функция
непрерывна в точке
![]() и
и
![]() ,
а функция
,
а функция
![]() непрерывна в точке
непрерывна в точке
![]() .
Тогда сложная функция
.
Тогда сложная функция
![]() непрерывна
в точке
.
непрерывна
в точке
.
Осн. лит.: 2, [86-126], 19, [162-180], 18, [46-189]
Доп. лит.: 30, [151-168].
Контрольные вопросы:
1. Сформулируйте определения предела функции при стремлении аргумента к некоторому конечному пределу и предела функции при стремлении аргумента к бесконечности.
2.Первый замечательный предел. Сформулируйте определение числа е (второй замечательный предел).
3.Сформулируйте определения непрерывности функции в точке и на отрезке. Какие точки называются точками разрыва функции.
Лекция № 8. Дифференциальное исчисление. Производная
Пусть в некоторой
окрестности точки
![]() и в самой точке
определена функция
и в самой точке
определена функция
![]() .
.
Определение:
Приращением аргумента х
в точке
![]() называется разность
называется разность
![]() .
.
Определение.
Приращением функции
![]() в точке
называется разность
в точке
называется разность
![]() .
.
Это приращение
зависит от двух аргументов
![]() и x.
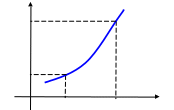
Геометрически x
и f
означают изменения абсциссы и ординаты
точки на графике
при перемещении из точки
и x.
Геометрически x
и f
означают изменения абсциссы и ординаты
точки на графике
при перемещении из точки
![]() в точку
в точку
![]() (рисунок 1).
(рисунок 1).
 Y
Y
![]()
![]() B
B
А
0
![]()
![]()
![]() X
X
Рис.1
Пример. Если
![]() ,
то
,
то
![]() ,
т. е. при увеличении стороны квадрата,
равной 1 на 0,1, его площадь возрастает
на 0,21.
,
т. е. при увеличении стороны квадрата,
равной 1 на 0,1, его площадь возрастает
на 0,21.
Используя понятия
x,
y,
можно дать ещё одно определение
непрерывности функции в точке
![]() ,
эквивалентное предыдущему.
,
эквивалентное предыдущему.
Определение.
Если функция
определена в некоторой окрестности
точки
и
![]() ,
то она называется непрерывной
в точке
.
,
то она называется непрерывной
в точке
.
В самом деле, этот предел означает, что
![]() ,
т. е.
,
т. е.
![]() .
.
Определение. Если существует предел
![]() ,
,
то это число называется производной функции в точке .
Эта производная обозначается также одним из следующих символов:
![]() .
.
Этот предел можно записывать также в виде
![]()
Определение.
Функция
называется дифференцируемой
в точке
![]() ,
если она имеет конечную производную в
этой точке.
,
если она имеет конечную производную в
этой точке.
Выясним теперь связь между дифференцируемостью и непрерывностью функции, для этого из определения выразим f.
![]() ,
,
(где
![]() -
б.м. при
-
б.м. при
![]() .
.
Следовательно,
![]() .
.
Теорема. Если функция дифференцируема в точке , то она непрерывна в этой точке
Основные правила дифференцирования
Теорема 1.
(правила дифференцирования суммы,
произведения и частного). Если
функции
![]() и
и
![]() дифференцируемы в точке x,
то сумма, произведение и частное этих
функций (частное при условии, что
дифференцируемы в точке x,
то сумма, произведение и частное этих
функций (частное при условии, что
![]() )
также дифференцируемы в этой точке и
имеют место следующие формулы:
)
также дифференцируемы в этой точке и
имеют место следующие формулы:
1.
![]()
2.
![]()
3.
![]() .
.
Производная сложной функции и обратной функций
