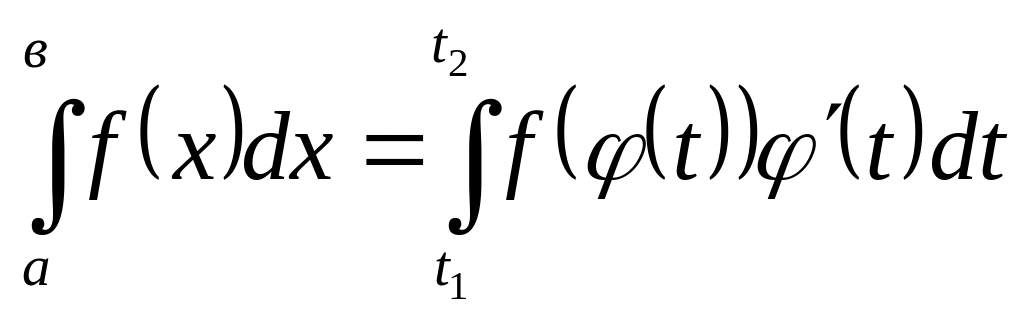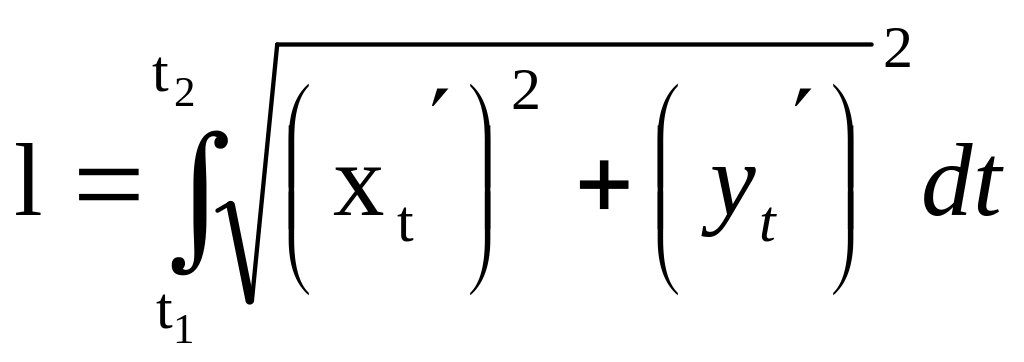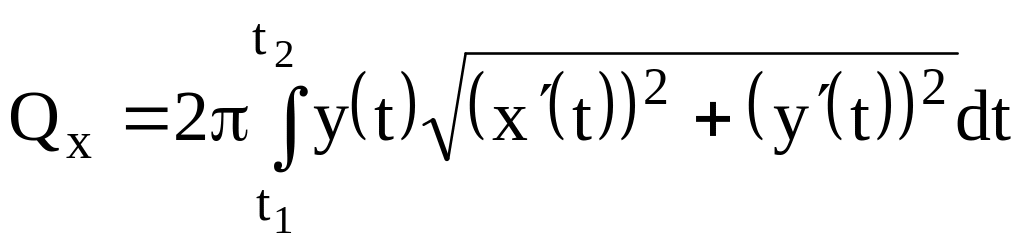2.9 Экзаменационные вопросы по курсу

№

п/п

Новые понятия

Содержание

1

2

3

1.

Матрица размера m n.

называется прямоугольная таблица чисел, состоящая из m строк и n столбцов.

2

Определитель матрицы

-это число, которое по определённому правилу сопоставляется каждой квадратной матрице. Определитель обозначается вертикальными линиями:

3

Вычисление определителя 2-го порядка

4

Вычисление определителя 3-го порядка

5

Транспонированная матрица

для матрицы A называется матрица A^T, столбцами которой являются соответствующие строки матрицы A.

6

Минор элемента

называется определитель, составленный из элементов, оставшихся после вычеркивания i-ой стоки и j-го столбца, на пересечении которых находится этот элемент и обозначается

8

Алгебраическое дополнение элемента

называется соответствующий минор, умноженный на т.е A_ij=(–1)^i+j M_ij, где i -номер cтроки и j –номер столбца, на пересечении которых находится данный элемент.

9

Диагональная матрица

квадратная матрица, у которой вне главной диагонали стоят нулевые элементы.

10

Единичная матрица

это диагональная матрица, у которой на главной диагонали стоят только единичные элементы

11

Произведение матрицы A размера mn на матрицу B размера nk

называется матрица C размера mk, каждый элемент c_ij которой равен произведению i –ой строки матрицы A на i–ый столбец матрицы B, т.е.

12

Обратная матрица

для квадратной матрицы A называется такая матрица A^-1, что выполняется равенство AA^-1=A^-1A=E.

13

Вырожденная и невырожденная матрицы

квадратная матрица A, определитель которой равен нулю, называется вырожденной, матрица, определитель которой не равен нулю, называется невырожденной.

14

Присоединённая матрица

для квадратной матрицы A называется матрица , элементами которой являются алгебраические дополнения соответствующих элементов матрицы A, т.е.

15

Ранг матрицы A

называется наибольший из порядков ее миноров, не равных нулю..Он обозначается символом r(A) или rangA.

16

Базисный минор

называется любой из отличных от нуля миноров матрицы А, порядок которого равен r (A).

17

Линейная зависимость строк

строки матрицы называются линейно зависимыми, если существуют такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

, где 0=(0 0 …0).

18

Линейная независимость строк

если линейная комбинация равна нулю тогда и только тогда, когда все коэффициенты равны нулю, т.е. , то строки называются линейно независимыми.

19

Матричная форма записи системы.

20

Формулы Крамера.

, . A=0 и _i – определитель матрицы системы, в которой вместо i-го столбца подставлен столбец свободных членов.

21

Расширенная матрица

называется матрица, полученная из матрицы системы приписыванием справа столбца свободных членов системы.

22

Однородная система линейных алгебраических уравнений

cистема, в которой все свободные члены нулевые.

23

Декартовая системой координат (Д.С.К.) на плоскости

пара взаимно перпендикулярных координатных осей на этой плоскости, пересекающиеся и общем начале координат точке O и имеющие равные масштабные отрезки. Первая из этих осей называется осью абсцисс (Ox) а вторая – осью ординат (Oy).

24

Д.С.К. в пространстве Oxyz

тройка взаимно перпендикулярных осей координат, пересекающихся в общем начале координат точке O и имеющих равные масштабные отрезки. Третья ось при этом называется осью аппликат (Oz).

25

Расстояние между точками A(x_A,y_A,z_A) и B(x_B,y_B,z_B) в пространстве

26

Вектор

отрезок с выбранным направлением, или направленный отрезок.

27

Коллинеарные вектора

вектора, лежащие на параллельных прямых (или на одной и той же прямой)

28

Компланарные вектора

Вектора, лежащие в одной плоскости или в параллельных плоскостях.

29

Линейные операции над векторами

это умножение вектора на число и сложение векторов

30

Линейная комбинация векторов

вектор C₁ +C₂ +...+C_n .

31

Линейно зависимые

векторы , ,...,

если существуют такие числа C₁,C₂,...,C_n , не равные одновременно нулю, что C₁ +C₂ +...+C_n =0

32

Линейно независимыми

векторы , ,...,

если существуют такие числа C₁,C₂,...,C_n , равные одновременно нулю, что C₁ +C₂ +...+C_n =0

33

Базисные вектора

совокупность n линейно независимых векторов

34

Скалярное произведение векторов и

число, равное произведению модулей этих векторов на косинус угла между ними, т. е. .

35

Формула вычисления скаляр-ного произведения векторов = и =

.

36

Формула вычисления угла между векторами и

37

Условие перпендикулярности (ортогональности) двух векторов.

.

38

Направляющие косинусы вектора

; ;

.

39

Орт вектора .

вектор координаты которого совпадают с направляющими косинусами вектора т.е. =( ).

40

Векторное произведение векторов и

вектор , удовлетворяющий трём условиям:

а) Модуль вектора равен произведению модулей векторов и на синус угла между ними:

sin

в) перпендикулярен векторам и  т.е. он перпендикулярен плоскости, проходящей через вектора и .

с) Тройка векторов правая

41

Формула вычисления вектор-ного произведения векторов и .

42

Площадь параллелограмма построенного на векторах и ,

43

Площадь треугольника, построенного на этих векторах, равна:

.

44

Смешанное произведение трех векторов

число, равное скалярному произведению векторного произведения векторов с вектором .

.

45

Формула вычисления век-торного произведения век-торов и ,

.

46

Объем параллелепипеда построенного на векторах

.

47

Объем тетраэдра (треугольной пирамиды)

.

48

Условие компланарности трех векторов.

49

Уравнение прямой с угловым коэффициентом к

50

Уравнение прямой, проходя-щей через данную точку с угловым коэффициентом к

51

Тангенс угла между прямыми и

52

Условие параллельности двух прямых

53

Условие перпендикулярности двух прямых

54

Направляющий вектор

любой ненулевой вектор на прямой

55

Параметрическое уравнениями прямой

56

Уравнение прямой с направляющим вектором.

57

Уравнение прямой, проходя-щей через две заданные точки

58

Общее уравнение прямой

59

Нормальный вектор прямой L

Вектор перпендикулярный прямой

60

Формула вычисления угла между прямыми

.

61

Условие перпендикулярности прямых

62

Условие параллельности прямых

.

63

Уравнение прямой с нормальным вектором.

.

64

Уравнением прямой в отрезках

65

Нормальное уравнение прямой

66

Расстояние от точки до прямой

.

67

Уравнением плоскости, проходящей через три заданные точки.

.

68

Общее уравнение плоскости

.

69

Уравнение плоскости с нормальным вектором.

.

70

Формула косинус угла между плоскостями и

с нормальными векторами и

71

Условие перпендикулярности плоскостей

.

72

Условие параллельности плоскостей

.

73

Уравнение плоскости в отрезках

.

74

Нормальное уравнение плоскости.

.

75

Формула расстояния от точки до плоскости

.

76

Параметрическими уравнениями прямой в пространстве.

77

Канонические уравнения прямой в пространстве.

.

78

Формула косинус угла между прямыми

и

.

79

Условие перпендикулярности прямых

.

80

Условие параллельности

.

81

Формула синус угла между плоскостью и прямой

82

Условие перпендикулярности прямой и плоскости

.

83

Условие параллельности прямой и плоскости

.

84

Общее уравнение прямой

.

85

Эллипс

это геометрическое место точек плоскости, сумма расстояний, от которых до двух выбранных фокусов, постоянна и равна

86

Каноническое уравнение эллипса

, .

87

Эксцентриситетом

число равное ,

88

Фокальная ось

ось, проходящая через фокусы эллипса

89

Директрисы эллипса

прямые, проходящие перпендикулярно фокальной оси на расстоянии от центра эллипса

90

Уравнение окружности радиуса а с центром в точке

: .

91

Гипербола

Это геометрическое место точек плоскости, разность расстояний от которых до двух выбранных фокусов постоянна

92

Каноническое уравнение гиперболы

, .

93

Асимптота кривой

прямая, у которой расстояние от точки на кривой до этой прямой стремится к нулю при удалении точки вдоль кривой в бесконечность.

94

Парабола

это геометрическое место точек плоскости, расстояние от которых до фокуса совпадает с расстоянием до директрисы

95

Каноническое уравнение параболы

. параметр параболы..

96

Общее уравнение кривой второго порядка

.

97

Эллиптический цилиндр

98

Гиперболический цилиндр

99

Параболический цилиндр

100

Каноническое уравнение конуса второго порядка.

101

Эллипсоид

, числа –полуоси

102

Уравнение сферы

.

103

Двуполостный гиперболоид

104

Однополостный гиперболоид.

105

Эллиптический параболоид

106

Гиперболический параболоид

107

Седловая поверхность

108

Уравнение поверхности второго порядка

109

Последовательность

переменная величина, значения которой можно перенумеровать:

110

Функция

Переменная величина у есть функция переменной величины если каждому значению по некоторому правилу поставлено в соответствие определенное значение у; запись

111

Область определения функции

множество (область) значений аргумента

112

Область значений функции

Множество значений, принимаемых функцией

113

График функции

Множества точек на плоскости, абсциссами которых являются значения аргумента, а ординатами значения функции, соответствующие этим значениям аргумента; множество точек

114

Предел переменной величины

Число есть предел переменной величины ,если для любого , начиная с некоторого момента в изменении , выполняется неравенство ; запись

115

Предел последовательности

если для найдется такой номер , что при будет

116

Предел функции на бесконечности

, если для найдется такое ,что при

117

Предел функции в точке

, если для найдется такое , что для , лежащего в окрестности и , выполняется неравенство

118

Два замечательных предела

(первый замечательный предел) (второй замечательный предел)

119

Непрерывность функции в точке

Функция непрерывна в точке , если ;

Другое определение: пусть (приращение аргумента) и (приращение функции). Функция непрерывна в точке , если б.м. приращению аргумента соответствует б.м. приращение функции

120

Производная функции в точке

предел отношения приращения функции к приращению аргумента, когда приращения аргумента стремится к нулю

121

Геометрический смысл производной

-тангенс угла наклона касательной к графику функции , проведенной в точке

122

Механическая интерпретация производной

скорость изменение функции в точке (относительно изменения аргумента ); если зависимость пути от времени, то (производная пути по времени)-скорость движения в момент t

123

Дифференциал функции

Дифференциал есть главная часть приращения функции, пропорциональная приращению аргумента ; б.м. высшего порядка относительно

124

Дифференциал независимой переменной

То же, что произвольное приращение независимой переменной

125

Геометрический смысл дифференциала функции

Дифференциал -приращение ординаты касательной прямой, проведенной к графику функции в точке

126

Дифференцируемая функция

Функция дифференцируема в точке , если существует конечная производная существует дифференциал ;

Дифференцируемая в функция непрерывна в , обратное неверно

127

Сложная функция (функция от функции) и ее производная

, где , т.е. сложная функция,

128

Инвариантность формы дифференциала

Для дифференциала форма записи дифференциала функции не зависит от того, будет ли независимым переменным или промежуточным аргументом

129

Обратная функция и ее дифференцирование

если разрешить относительно , то обратная функция к . Производные обратных функций являются взаимно обратными величинами:

130

Параметрическое задание функции. Дифференцирование параметрически заданных уравнений

Связь между аргументом и функцией выражена через посредство третьей переменной -параметра: и заданы как функции параметра: ; производная: , если

131

Монотонные функции

Функции возрастающие или убывающие. Функция возрастает (убывает), если большему значению аргумента соответствует большее (меньшее) значение функции

132

Признак возрастания или убывания

-функция возрастает, убывает

133

Точки максимума, минимума, экстремума

Точка - точка максимума (минимума) функции , если значение больше (меньше) всех значений , принимаемых в некоторой окрестности ; определение подчеркивает локальный характер понятие; точка экстремума - общее название точек максимума и минимума

134

Необходимый признак экстремума (признак Ферма)

Если в точке экстремума производная существует, то она равна нулю

135

Достаточный признак экстремума

Если производная при переходе через меняет знак на - , то - точка максимума, если с - на , то - точка минимума

136

Асимптоты и их отыскание

прямая L называется асимптотой кривой, если расстояние от точки на кривой до L стремится к нулю, когда точка неограниченно удаляется от начала координат; если , то прямая - вертикальная асимптота графика ; прямая - наклонная асимптота (в частности, при - горизонтальная) , ,

137

Выпуклость (вогнутость) кривой

Кривая выпукла (вогнута), если лежит над (под) любой своей касательной

138

Признак выпуклости (вогнутости)

выпукла, -вогнута

139

Точка перегиба

Точка на кривой, которая отделяет участок выпуклости от участка вогнутости

140

Признаки точки перегиба

или «не существует» - необходимый признак, меняет знак при переходе через точку , тогда в т. перегиб - достаточный признак

141

Теорема о хорде и касательной

Если у кривой линии в каждой ее точке существует касательная, то найдется точка, в которой касательная параллельна хорде

142

Теорема (формула) Лагранжа

Специальный случай теоремы о хорде и касательной для графика функции на и существует то найдется точка , такая, что

143

Теорема Ролля

Специальный случай теоремы Лагранжа: если и существует то Теоремы Лагранжа и Ролля верны для функции , непрерывной на и дифференцируемой по крайней мере на

144

Теорема Коши

Если и непрерывны на и дифференцируемы на , причем , то

145

Формула Тейлора

Представление функции, имеющей в окрестности производные до порядка в виде суммы многочлена степени расположенного по степеням и некоторого остаточного члена, содержащего в степени

146

Первообразная функции

Функция называется первообразной для функции на некотором промежутке, если для всех значений из этого промежутка выполняется равенство

147

Неопределенный интеграл

Если -первообразная функции для , то выражение , где -произвольная постоянная, называется неопределенным интегралом от функции и обозначается , т.е

148

Формула замены переменной в неопределенном интеграле.

Пусть где монотонна и дифференцируема . Тогда

149

Формула интегрирования по частям

150

Рекуррентная формула для интеграла

151

Вычисление интегралов вида

Выделить полный квадрат из трехчлена

Применить подстановку

152

Интегрирование рациональных функции где многочлены

1) если дробь неправильная, то выделить целую часть; 2) разложить многочлен на множители;

3) правильную дробь представить в виде суммы простых дробей;

4) найти неизвестные коэффициенты методом частных значений и методом неопределенных коэффициентов;

5) вычислить интегралы от простых дробей.

152

Интегралы вида

где -рациональная функция; целые положительные числа

Замена , где -общий знаменатель дробей

153

Интегралы вида

1)

2)

3)

Осуществляется замена:

1)

2)

3)

154

Интегралы вида

где m,n-целые числа.

1)Пусть хотя бы один из показателей m или nбудут нечетным, целым, положительным. Тогда полагаем если m-нечетное число; , если n-нечетное число.

2) Пусть оба показателя четные, положительные числа. Тогда применяются формулы

3) Пусть четное отрицательное целое число. Тогда полагаем

155

Интегралы вида

где -рациональная функция относительно .

Полагаем (универсальная подстановка). Тогда . Частные подстановки:

1) пусть тогда полагаем

2) пусть тогда полагаем ;

3) пусть тогда полагаем

156

Определение определенного интеграла

Если существует конечный предел интегральной суммы при не зависящий ни от способа дробления промежутка на части, ни от выбора точек то тот предел называют определенным интегралом функций по промежутку ,

157

Формула Ньютона-Лейбница

где ^-первообразная функций

158

Формула интегрирования по частям для определенного интеграла

Пусть производные непрерывна на отрезке , тогда

159

Замена переменной в определенном интеграле

Если функция непрерывна на отрезке и функция непрерывна дифференцируема на отрезке

причем то

160

Площадь криволинейной трапеции, ограниченной кривой , прямыми

161

Площадь фигуры, ограниченной кривыми

162

Площадь фигуры, ограниченной кривой, имеющей параметрическое уравнение

163

Площадь фигуры, ограниченной графиком функции и двумя лучами

164

Длина дуги кривой, заданной

уравнением

165

Длина дуги кривой, заданной параметрическими уравнениями

166

Длина дуги пространственной кривой, заданной параметрическими уравнениями

167

Длина дуги кривой, заданной полярными уравнением

168

Площадь поверхности, образо-ванной вращением вокруг оси , дуги кривой, заданной функцией

169

Площадь поверхности, образо-ванной вращением вокруг оси дуги, заданной параметрами уравнениями

170

Площадь поверхности, образованной вращением вокруг оси дуги, заданной в полярных координатах
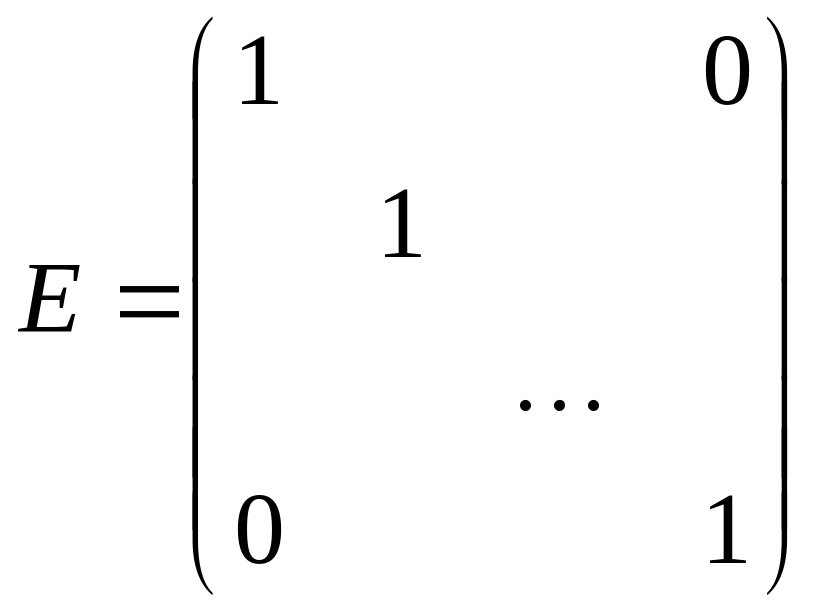
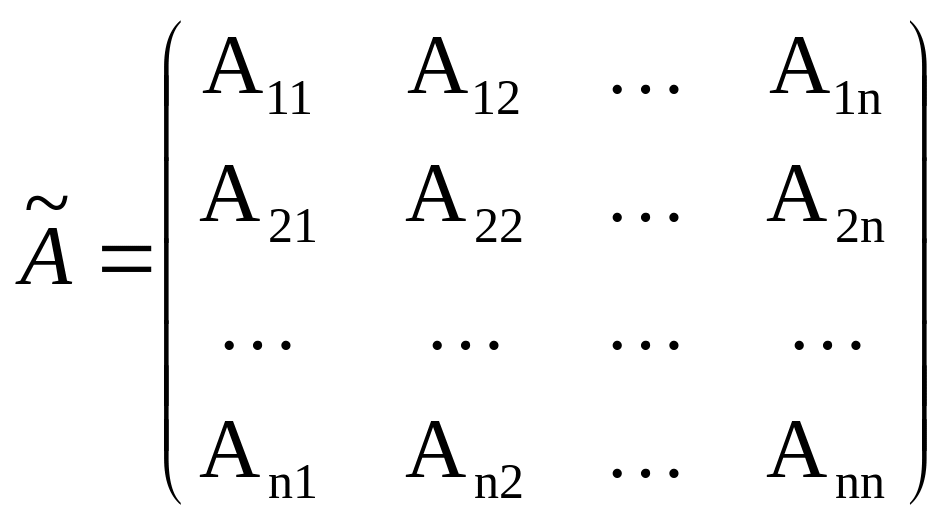
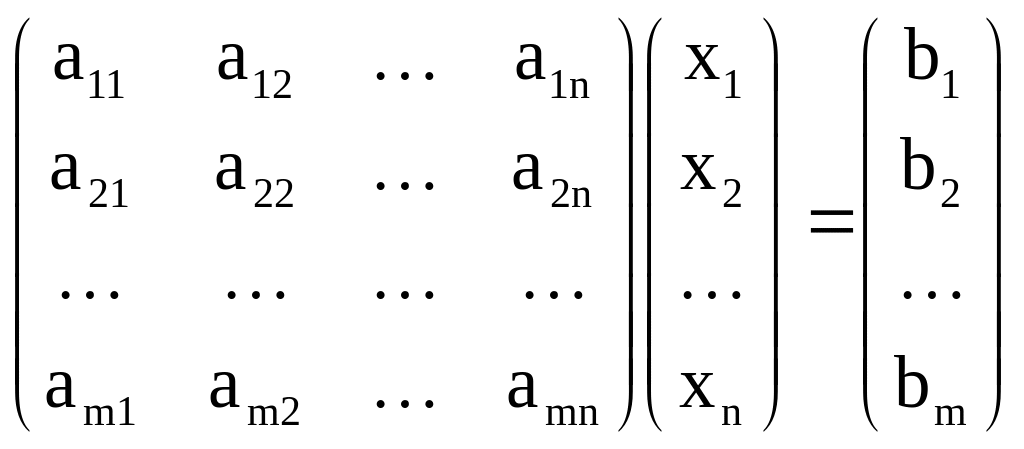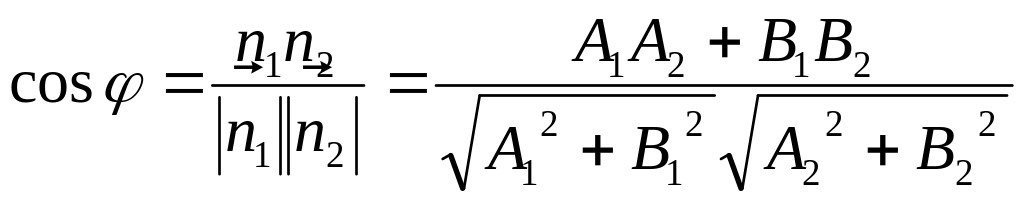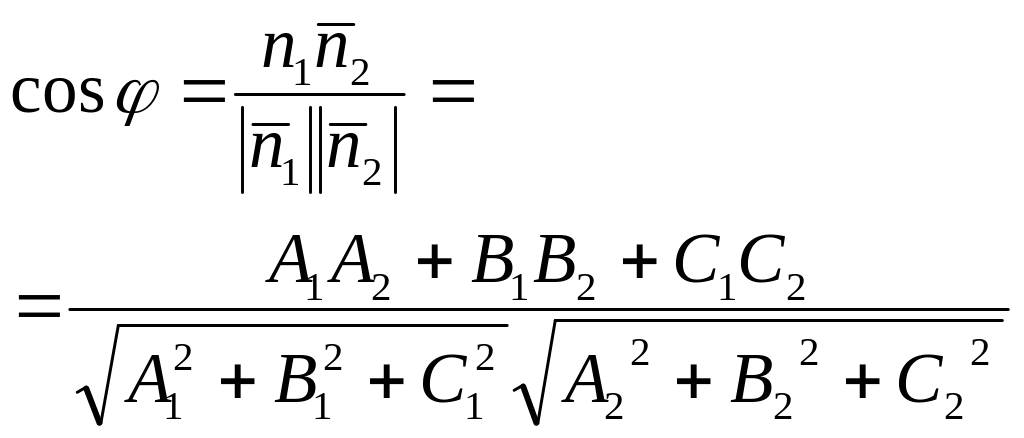
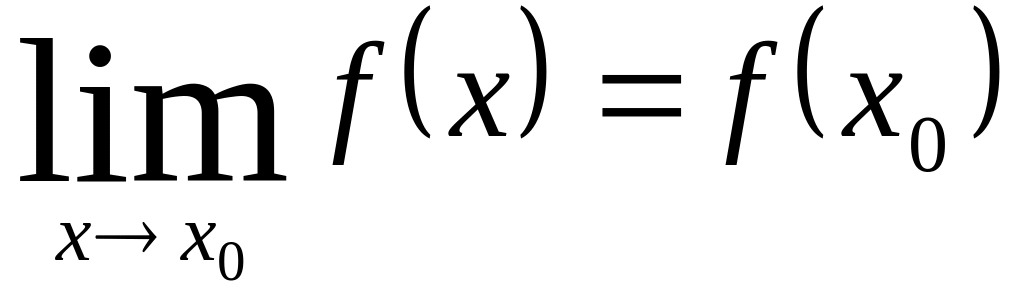