4.13.4. Монотонные функции

На множестве двоичных наборов длины n определим отношение предшествования наборов.

Пусть и . Тогда набор предшествует набору , если .

Отношение предшествования наборов обозначается как , т.е. значение каждой компоненты предшествующего набора не превосходит значения соответствующей компоненты следующего набора.

Например, наборы (0, 1, 0, 0, 1, 0) и (0, 1, 1, 0, 1, 1) находятся в отношении предшествования, а наборы (1, 1, 0, 0, 1, 0) и (1, 0, 1, 0, 1, 1) оказываются несравнимыми в отношении .

Упражнение. Проверить, что отношение предшествования наборов является отношением частичного порядка.

Рассмотрим представление отношения на множестве с помощью диаграммы для этого отношения, представленной на рис 4.6. Пусть n = 3.

1 1 1

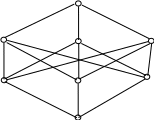
0 1 1 1 0 1 1 1 0

1 0 0 0 1 0 0 0 1

0 0 0

Рис. 4.6

На приведенной диаграмме не указана ориентация дуг, которые всегда считаются ориентированными в направлении верхней из двух вершин, соединяемых дугой.

Все наборы единичного n-мерного куба, имеющие равное число единиц, несравнимы между собой и образуют слой в таком кубе. В случае произвольного значения n в диаграмме для отношения содержится n + 1 слоев.

Упражнение. Нарисовать диаграмму отношения для n = 4.

Определение

Булевская функция f(x₁, . . . , x_n) называется монотонной, если для любых наборов и , для которых , справедливо неравенство .

Множество всех монотонных булевских функций обозначается как M.

Примеры.

1. Функция f (x₁, x₂)= x₁  x₂ немонотонна, так как

(0, 0) (1, 0), но f(0, 0) > f (1, 0).

2. Функции & и являются монотонными.

Множество всех монотонных функций является замкнутым классом. Поскольку тождественная функция f(x) = x  монотонна, то для доказательства замкнутости M достаточно проверить, что при

h = (1),

где f, g₁ ,..., g _n  монотонные функции, M.

Пусть x₁, . . . , x_n все различные символы переменных, которые встречаются в формуле (1). Возьмем два набора и значений этих переменных, для которых . Тогда для наборов и , составленных из значений переменных функций g₁, . . . , g_n, взятых из наборов и , справедливы соотношения:

Следовательно, для i = 1, . . . , n. Поэтому . Поскольку M, то , т.е. . Поэтому M.

Замечание. Доказанное свойство монотонных функций позволяет просто устанавливать монотонность функций, представленных формулами составленными из монотонных функций. Например, монотонной является функция, представляемая формулой

.

Простейшей немонотонной функцией можно считать функцию , поскольку три остальные функции одной переменной являются монотонными. Покажем, что отрицание (или простейшая немонотонная функция) может быть получено из всякой немонотонной функции. Последнее свойство можно сформулировать иначе: всякая немонотонная функция содержит отрицание, которое может быть выражено из этой функции.

Лемма. (О немонотонной функции)

Если M, то подстановкой вместо переменных этой функции функций-констант и тождественной функции f(x) = x можно получить функцию .

Доказательство

Пусть f(x₁,...,x_n) M. Тогда найдутся такие два набора и значений переменных x₁, . . . , x_n, что и . Возьмем эти наборы. Предположим, что они различаются в k компонентах.

Построим цепочку двоичных наборов, последовательно заменяя значения 0, 1, . . . , k разрядов, в которых набор отличается от набора :

. (1)

Очевидно, что всякие два соседних набора этой последовательности различаются ровно в одной компоненте.

Рассмотрим значения f на наборах цепочки (1).

. (2)

Поскольку и , то в (2) найдутся последовательно идущие значения 1 и 0.

Рассмотрим наборы = и = = , на которых функция f принимает значения 1 и 0.

Тогда .

Действительно,

h (0) = h = 1 и

h (1) = h )= 0.

Доказательство окончено.

Замечание. Двоичные наборы, различающиеся лишь в одной компоненте, называются соседними. Доказательство последней леммы позволяет утверждать, что для всякой немонотонной функции найдутся таких два соседних набора, на которых нарушается монотонность.

Рассмотрим пример использования леммы о немонотонной функции. Пусть задана функция f = x₁  (x₂  x₃). Тогда наборы (0, 1, 0) и (1, 1, 0) являются соседними и на этих наборах нарушается монотонность f:

f(0, 1, 0) = 1 и f(1, 1, 0) = 0.

Поэтому f(x, 1, 0) = .

Упражнение.

1. Докажите утверждение, обратное утверждению, сформулированному в лемме о немонотонной функции.

2. Проверьте справедливость следующего утверждения: Если ф.а.л. f(x₁,...,x_n) отлична от тождественной единицы, то всякая минимальная ДНФ для f не содержит элементарных конъюнкций, содержащих отрицания переменных.