26.Классификация кривых второго порядка

Рассмотрим уравнение Ax²+By²+Cxy+Dx+Ey+F=0 (*) (A²+B²+C² не равно 0)

Теорема: для любой кривой второго порядка, заданной уравнением* существует прямоугольная ск, в которой уравнение кривой имеет один из следующих видов:

1) Эллипс

2) Гипербола

3) Парабола

4) Линейный эллипс

5) Вырожденный эллипс(точка (0;0))

6) Пара пересекающихся прямых

7) Пара параллельных прямых

8) Пара совпадающих прямых

9) Пара мнимых прямых(пустое множество)

25. Парабола

Опр. Пусть на пл. задана точка F и прямая., не проходящая через ту точку – d(директриса)

Парабола – множество точек в плоскости, удовлетворяющее условию: MF=ρ(M,d)

Составим уравнение: проведем ось 0х через F(фокус) перпендикулярно d

Начало корд. – середина торезка между F и т. Пересеч. x и d

Пусть ρ(F,d)=p=const, F(p/2;0), d: x=-p/2. MF=ρ(M,d) , ρ(M,d)=x + p/2

Пусть M(x;y) - произвольная точка параболы, /(^2), (p/2 - x)² + y²=x² + 2px/2 + p²/4

P – параметр параболы y² = 2px – каноническое уравнение параболы. (0;0) – вершина праболы. 0х – ось симметрии

Парабола- неограниченная кривая, лежащая в плоскости х≥0

24. Гипербола

Пусть на пл-и заданы 2 точки F1 и F2(фокусы) и число 2а>0.

Гипербола – множество точек, удовлетворяющее условию: модуль разности расстояний от произвольной точки гиперболы до фокусов есть величина постоянная и равная 2а. |MF1 – MF2|=2a

Обозначим MF₁=r₁, MF₂ = r₂, F₁F₂ = 2c -фокусное расстояние

По правилу треугольника r₁ + 2c≥r₂, r₂ + 2_c≥r₁ => 2c≥r₂-r₁ 2c≥r₁-r₂. |r₁-r₂|=|r₂-r₁|=2a, 2c≥2a => c≥a для гиперболы

Введем прямоуг. Ск. Проведем Ох через F1 и F2. 0у перпендикул. 0х. F1(-c;0), F2(c;0) ] M(x;y)- произвольная т. гиперб. |MF1-MF2|=2a

,

- уравнение гиперболы

. . . , Пусть с>a, c²-a²>0, c² - a² = b²

- каноническое уравнение гиперболы

Свойства гиперболы: 1) 0х и 0у – оси симметрии, начало корд. – центр симметрии. Точки (±а;0) принадл. Гиперболе и явл. Точками ее пересечения с 0х. а – действительная полуось гиперболы, в – мнимая-//-. в²=с²-а², e=c/a≥1(эксцентриситет).

Прямые с уравнением y=±b/a*x – асимптоты гиперболы

Алгоритм построения гиперболы: 1.строим основной прямоугольник 2a*2b 2. отмечаем вершины и фокусы 3. строим асимптоты 4. проводим гиперболу через вершины, учитывая асимптоты

Директрисы эллипса и гиперболы Опр. – прямая, которая обозначается α и удовлетворяет условию: , M – произвольная точка кривой, е – эксцентриситет, F – один из фокусов, d – соответствующая директриса т.е. ,

Уравнение директрисы:

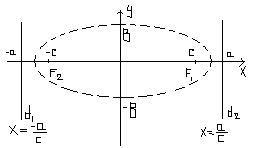
23. Эллипс

Опр. – пусть на пл-и зафиксированы 2 точки F1 и F2.

Эллипс- множество точек пл-и, сумма расстояний до которых от точек F1 и F2 есть величина постоянная:MF1+MF2=2a=const, где М – произвольная т. эллипса, точки F1, F2 – фокусы эллипса

F1F2 – фокусное расстояние эллипса (обозначается 2с)

F1F2 ≤ MF1 + MF2, т.е. 2с ≤ 2а. Для эллипса а≥с

Составим уравнение эллипса: введем ск Ось 0х проведем через фокусы F1 и F2. пусть О–середина отрезка F1F2=2c =>

=>F1(-c;0), F2(c;0). Пусть М(х;у) – произвольная точка эллипса. Из определения эллипса MF1 + MF2 = 2a

,

- уравнение эллипса. Преобразим его:

Переносишь один корень вправо и в квадрат. Оставляешь в одной стороне корень и снова в квадрат. Получаем:

a⁴+c²x²=a²c²+a²x²+a²y² => x²(c²-a²)-a²y²=a²(c²-a²)|/a²(c²-a²)≠0 => => , т.к. a>c, то а² – с² > 0. a² - c² обозначим b² - каноническое уравнение эллипса

Свойства эллипса: 1. точки с корд. (а;0), (-а;0), (0;b), (0;-b) называются его вершинами

2. переменные х и у входят в уравнение в четных степенях т.е. 0х и 0у – оси симметрии

3. начало координат – ценр симметрии т.е. если т. М1(х;у)Єэллипсу, то М2(-х;у), М3(х;-у), М4(-х;-у) тоже т. эллипса

4. эллипс лежит в прямоугольнике со сторонами 2а*2b т.е.эллипс – это ограниченная кривая

5. отношение с/а=е≤1(е - эксцентриситет)

Пусть е=0 т.е. с=0. a² – c² = b²., a² – b² = c², c=0, a² = b² , x² + y² = a² – окружнотсь (при е =о)

e=1, то с=а эллипс вырождается в отрезок. е характеризует сплюснутость эллипса, чем ближе е к 1, тем больше сжатие