
- •1 Матрицы. Операции над матр.
- •2 Определители. Св-ва определ.
- •3 Обратная матрица
- •4 Системы линейных уравнений.
- •5 Системы линейных уравнений.
- •6 Свободный вектор. Линейные операции
- •8 Координаты вектора в базисе
- •10 Направляющие cos
- •11 Векторное произведение [a,b]
- •18 Уравнение с угловым коэффициентом. Угол между прямыми.
- •19 Расстоян от тчк до прямой
- •20 Плоскость
- •21 Канонич уравнение прямой. Условие параллелн-ти прямой и плоскости
- •22 Угол между плоскостями. Угол между прямой и плоск.
- •29. Параболоиды
- •28. Гиперболоиды
- •27. Эллипсоид. Конус
- •26.Классификация кривых второго порядка
- •25. Парабола
- •24. Гипербола
- •23. Эллипс
19 Расстоян от тчк до прямой
l:Ax+By+C=0
M(x0;y0)![]() р(M;l)=MK
р(M;l)=MK
![]()
20 Плоскость
Параметр уравнен
 выбирем
в R3
афф сист коор. Тчк F(x0;y0;z0)
– базис тчк, u={u1,…}
v=…
M(x,y,z).
u
и v
определяют положение плоскости в
пространстве.
выбирем
в R3
афф сист коор. Тчк F(x0;y0;z0)
– базис тчк, u={u1,…}
v=…
M(x,y,z).
u
и v
определяют положение плоскости в
пространстве.
OM=OF-FM, FM||P, u и v – базис
FM=tu+sv при t и s параметр в векторной форме OM=tu+sv+OF
Параметр уравн прямой через тчк(x0,y0,z0) и || u и v: x=tu1+sv1+x0 y=tu2+… z=…
Общее уравнен
Векторы FM, u, v – компланарны.
FM={x-x0;y-y0;z-zo}. Вычислим смешанное произведение, миноры обазначим: A,-B,C. A(x-x0)+B(y-y0)+c(z-z0)=Ax+By+Cz+D=0 при D=-(Ax0+By0+Cz0) лин уравн относит x,y,z P: Ax+By+Cz=0
Нормаль
N={A;B;C}={миноры}=это
вектор произвед [u;v]![]() n
перпенд P
нормаль к плоскости
n
перпенд P
нормаль к плоскости
Через 3 тчк.
Плоскость проходит
через М1,М2,М3. они не лежат на одной
прямой.![]() ,
но M1M,M1M2,M1M3
компланарны. (M1M,M1M2,M1M3)=0
,
но M1M,M1M2,M1M3
компланарны. (M1M,M1M2,M1M3)=0
|x-x1 y-y1 z-z1 x2-x1… x3-x1|=0
21 Канонич уравнение прямой. Условие параллелн-ти прямой и плоскости
![]() a||l,
F(x0;y0;z0)
– базис, a={m,n,p}
в параметрической форме l:x=tm+x0,
y=tn+y0,
… вырозим t.
Основ уравнен прямой через тчк(x0;y0;z0)
и || {M;N;P}:X-x0/m=y-y0/n=z-z0/p
a||l,
F(x0;y0;z0)
– базис, a={m,n,p}
в параметрической форме l:x=tm+x0,
y=tn+y0,
… вырозим t.
Основ уравнен прямой через тчк(x0;y0;z0)
и || {M;N;P}:X-x0/m=y-y0/n=z-z0/p
Условие параллел
P||l P: Ax+By+Cz=0 n={A;B;C} l=x-x0/m=y-y0/n=z-z0/p a={m,n,p}||l P||l только когда а перпердикул n. (a;n)=0
Услов паралел Am+Bn+Cz=0
22 Угол между плоскостями. Угол между прямой и плоск.
![]() P1:A1x+B1y+C1z+D1=0
P2:… угол
L=(P1^P2)=(n1^n2), n1={A1;B1;C1} n2=… .
P1:A1x+B1y+C1z+D1=0
P2:… угол
L=(P1^P2)=(n1^n2), n1={A1;B1;C1} n2=… .
![]() cosL=|n1,n2|/|n1||n2|
cosL=|n1,n2|/|n1||n2|
Между прямой и плоскост
![]() P:Ax+By+Cz=0
l:x-x0/m=y-yo/n=z-z0/p
угол между прямой и плоскостью это угол
между этой прямой и ее проекцией.
P:Ax+By+Cz=0
l:x-x0/m=y-yo/n=z-z0/p
угол между прямой и плоскостью это угол
между этой прямой и ее проекцией.
cosB=|(a,n)/|a||n||sinL
![]()
29. Параболоиды
1) Эллиптический параболоид
![]() p,q>0
p,q>0
Сечения: x=h,
![]()
![]() -
парабола
-
парабола
q
– параметр, q>0
ветви вверх, вершина:![]() ,
,
![]()
y=h
![]() ,
x
,
x![]() - парабола, р – параметр, ветви вверх
- парабола, р – параметр, ветви вверх
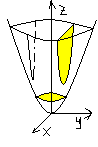 z=h
z=h
![]() h>0
– эллипс, h=0
– точка(0;0;0), h<0
– мнимый эллипс(пустое множество)
h>0
– эллипс, h=0
– точка(0;0;0), h<0
– мнимый эллипс(пустое множество)
2) Гиперболичекий параболоид
![]() ,
p,q>0
,
p,q>0
Сечения: x=h![]() ,
,
![]() -
парабола с параметром q,
ветви вниз
-
парабола с параметром q,
ветви вниз
Y=h
![]() ,
,
![]() - парабола с параметром р, ветви вверх
- парабола с параметром р, ветви вверх
 Z=h
Z=h
![]() ,
h=0
- гипербола , h
не равно 0 – пара пересекающихся прямых
,
h=0
- гипербола , h
не равно 0 – пара пересекающихся прямых
28. Гиперболоиды
1) Гиперболоид
однополостный – множество точек
пространства R3
, которое
в некоторой прямоугольной ск м.б. задано
уравнением:
![]()
Сечения: Пусть x=h
![]() при |h|
не равном а это гипербола. |h|=a,
то пара пересекающихся прямых
при |h|
не равном а это гипербола. |h|=a,
то пара пересекающихся прямых
При y=h аналогичное сечение
Пусть z=h
![]() - эллипс для любого h
- эллипс для любого h
 При
h=0
получаем так называемое горловое сечение
При
h=0
получаем так называемое горловое сечение
2) Гиперболоид
двухполостный – мнжество точек
пространства R3,
которое в некоторой прямоугольной ск
м.б. задано уравнением:
![]()
Сечения: x=h
![]() - гипербола для любого h, y=h
– аналогично
- гипербола для любого h, y=h
– аналогично
 Z=h.
|h|>c
– эллипс
Z=h.
|h|>c
– эллипс
![]() ,
|h|=c
– пара точек, |h|<c
– пустое множество
,
|h|=c
– пара точек, |h|<c
– пустое множество
27. Эллипсоид. Конус
1) Эллипсоид – множество точек пространства R3 в некоторой прямоугольной ск, удовлетворяющих уравнению:
![]() ,
xЄ(-a;a),
yЄ(-b;b),
zЄ(-c;c)
,
xЄ(-a;a),
yЄ(-b;b),
zЄ(-c;c)
Сечения: пусть
x=h:
![]() ,
|h|<0
- эллипсв сечении, |h|>a
– пустое множество, |h|=a
– точки (±а;0;0)
,
|h|<0
- эллипсв сечении, |h|>a
– пустое множество, |h|=a
– точки (±а;0;0)
Аналогично при y=h и z=h

2) Конус – множество точек в пространстве R3, которое в некоторой прямоугольной ск м.б. заданоуравнением:
![]()
Сечения: Пусть x=h
![]() .
Если h
не равно 0, то гипербола, если h=0,
то пара пересекающихся прямых
.
Если h
не равно 0, то гипербола, если h=0,
то пара пересекающихся прямых
При y=h аналогичные сечения
Пусть z
= h
![]() .
При h
не равном 0 – эллипс, при h=0
– точка (0;0;0)
.
При h
не равном 0 – эллипс, при h=0
– точка (0;0;0)

