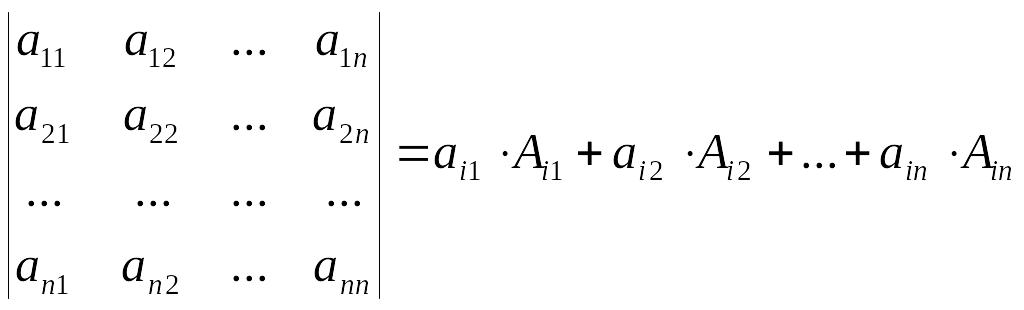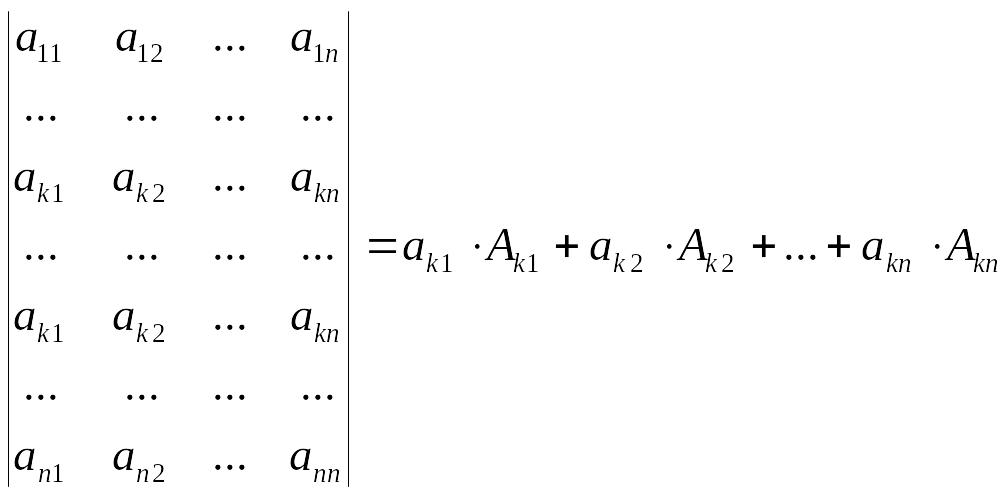2.3. Миноры и алгебраические дополнения

Вычисление определителей на основании данного выше определения представляет некоторые трудности. Существует более простой метод вычисления определителей, основанный на том, что определитель порядка n может быть выражен через определители более низких порядков.

Пусть дана квадратная матрица . Будем называть минором элемента матрицы А определитель (n-1)-го порядка, соответствующий матрице, которая получается из матрицы А вычеркиванием i–ой строки и j–го столбца. Минор элемента будем обозначать символом M_ij.

Например, , .

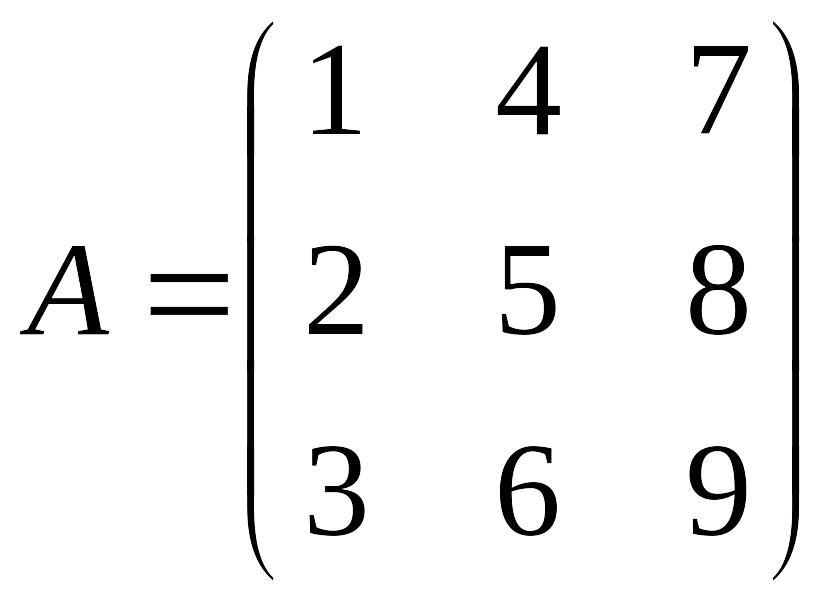Алгебраическим дополнением A элемента матрицы А называется его минор, взятый со знаком (-1) , т.е. .

Например, в предыдущей матрице .

Теорема. Произведение любого элемента a_ij на его алгебраическое дополнение в определителе |A| является алгебраической суммой, слагаемые которой будут некоторыми членами определителя |A|, причем их знаки в этой сумме совпадают с теми знаками, с которыми они входят в состав определителя.

Покажем сначала, что произведение является алгебраической суммой, слагаемые которой удовлетворяют условию теоремы.

В определителе

М занимает правый нижний угол. Число i+j является в этом случае четным и поэтому А₁₁=М₁₁.

Произвольный член

(2.3.1)

М₁₁ имеет в миноре М₁₁ знак , где есть число инверсий в подстановке .

Умножая на (2.3.1), получим произведение

(2.3.2)

элементов, расположенных в разных строках и разных столбцах определителя |A|. Поэтому каждое такое произведение (2.3.2) будет членом определителя |A|. Знаки членов (2.3.2) и (2.3.1) совпадают, так как знак члена (2.3.2) определяется выражением = . Такой же знак имеет каждый член (2.2.3) и в определителе |A|, так как четность подстановки , составленной из индексов этого члена, определяется выражением .

Перейдем к рассмотрению общего случая.

Переставляя соседние строки и столбцы определителя |A|, передвинем произвольный элемент a_ij в левый верхний угол. Для этой цели переставим i-ую строку на (i–1) раз и j-ый столбец на (j–1) раз. Очевидно, что при данной перестановке взаимное расположение строк и столбцов в миноре M_ij остается без изменения. После этих преобразований получим новый определитель |A | с тем же минором M_ij для элемента a_ij, но расположенный в правом нижнем углу определителя |A |.

Как доказано выше, произведение a_ij M_ij является суммой некоторого числа членов определителя |A |. Однако определитель |A | получен из определителя |A| путем (i+j-2) перестановок строк и столбцов, и поэтому члены определителя |A | отличаются от соответствующих членов определителя |A| лишь знаком . Отсюда следует, что произведение состоит из некоторого количества членов определителя |A|, взятых с такими же знаками, какие они имеют в этом определителе. Теорема доказана.

2.4. Вычисление определителей n-го порядка

Полученные в предыдущем параграфе результаты позволяют свести вычисление определителей порядка n к вычислению нескольких определителей порядка n-1.

Действительно, является суммой нескольких членов определителя |A|. Легко подсчитать число этих членов: оно равно числу членов в миноре , т.е. равно (n-1)!.

Рассмотрим теперь все произведения элементов i-ой строки на соответствующие им алгебраические дополнения, т.е. произведения

(2.4.1)

С одной стороны, никакой член определителя |A| не может войти в состав двух разных произведений (2.4.1), так как все члены определителя, входящие в любое произведение , содержат из i-й строки элемент и поэтому отличается от членов, входящих в остальные произведения.

С другой стороны, общее число членов определителя |A|, входящих во все произведения (2.3.1), равно , т.е. совпадает с числом членов определителя порядка n.

Таким образом, мы доказали, что имеет место следующая теорема.

Теорема. Определитель равен сумме произведений элементов любой его строки на их алгебраические дополнения, т.е.

(2.4.2)

Аналогично разложение определителя можно получить и по любому его столбцу.

Теорема. Сумма произведений элементов какой-либо строки (или какого-либо столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (другого столбца) равна нулю.

Перепишем выражение (2.4.2) в виде

(2.4.3)

так как алгебраические дополнения не зависит от элементов i-ой строки, то равенство (2.4.3) является тождеством относительно элементов .

Заменив элементы соответствующими элементами любой k-ой строки, , получим

(2.4.4)

Левая часть равенства (2.4.4) есть определитель, содержащий две одинаковые строки и, следовательно, равна нулю. Теорема доказана.

Вычисление определителей n-го порядка производится на основании соотношения (2.4.2) разложением определителя по элементам какой-либо строки или какого-либо столбца. В этом случае необходимо вычислить n определителей порядка n-1. Используя следствие 5, можно свести вычисления определителя порядка n к вычислению лишь одного определителя порядка (n-1). Для этого на основании следствия 5 необходимо так преобразовать определитель порядка n, чтобы некоторая строка (столбец) содержала только один ненулевой элемент.

Пример. Вычислить определитель.

.

Решение. На основании свойства определителей, именно следствия 5, преобразуем данный определитель следующим образом: из элементов второго столбца вычтем удвоенные соответствующие элементы первого столбца:

Элемент a₅₂ = 1 назовем направляющим элементом. Второй столбец преобразуем в единичный с единицей на месте направляющего элемента a₅₂. Для этого ко второй и к четвертой строкам прибавим направляющую пятую строку, соответственно умноженную на 1 и на 2.

Тогда

Разложим определитель по элементам второго столбца

.

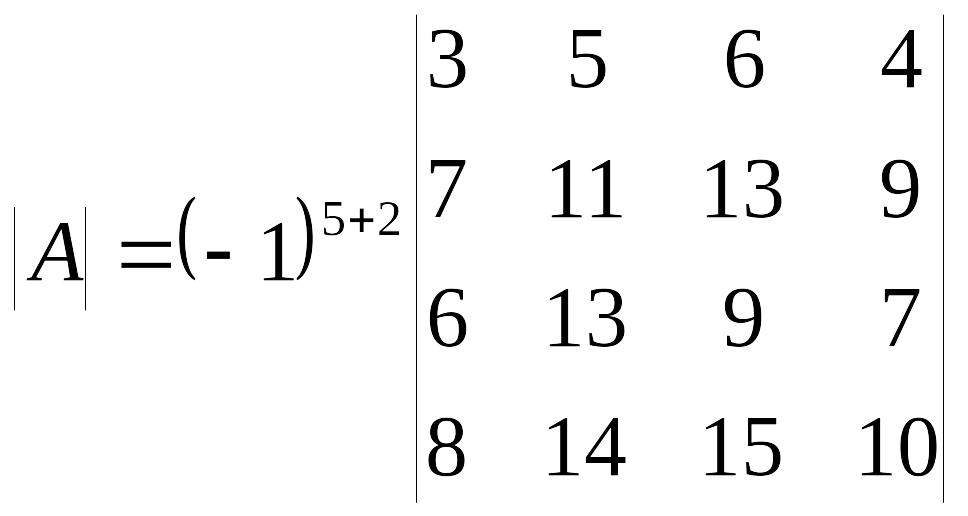Из элементов второй строки вычтем удвоенные соответствующие элементы первой строки

.

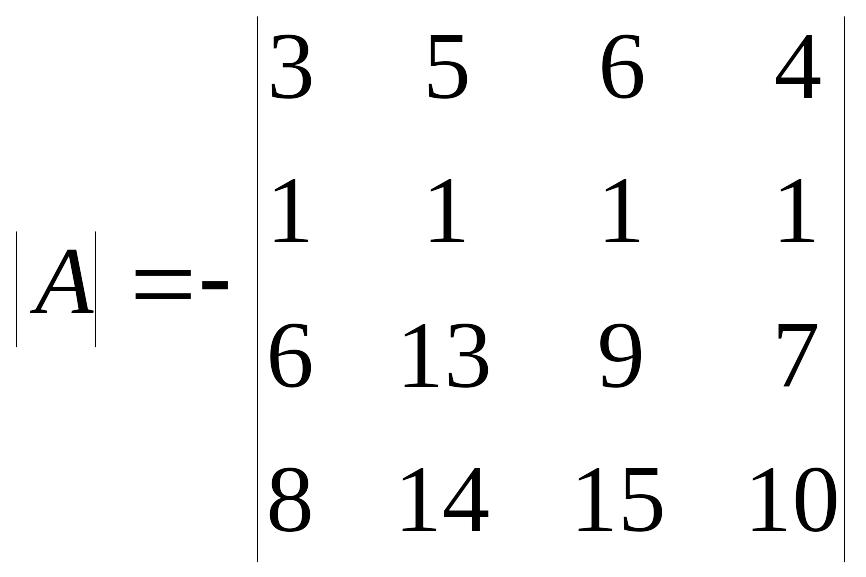Выбирая в качестве направляющего элемента элемент , преобразуем вторую строку в единичную. Для этого ко второму, третьему и четвертому столбцам прибавим первый столбец, умноженный на –1.

.

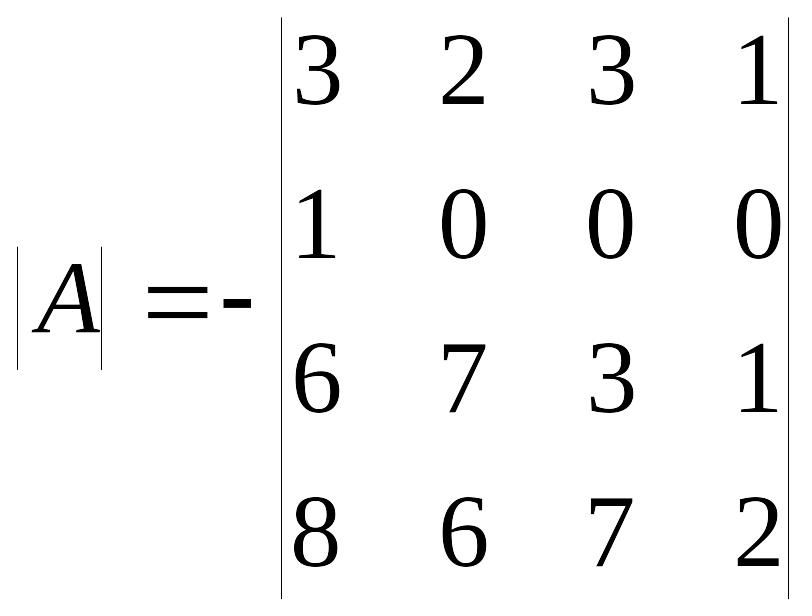Разложим определитель по элементам второй строки:

.

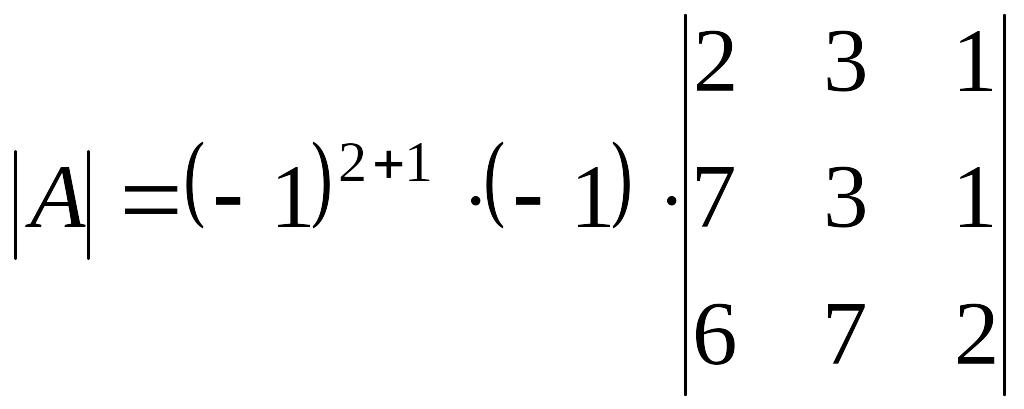Вычтем из второй строки первую и разложим определитель по элементам второй строки. В результате получим

.
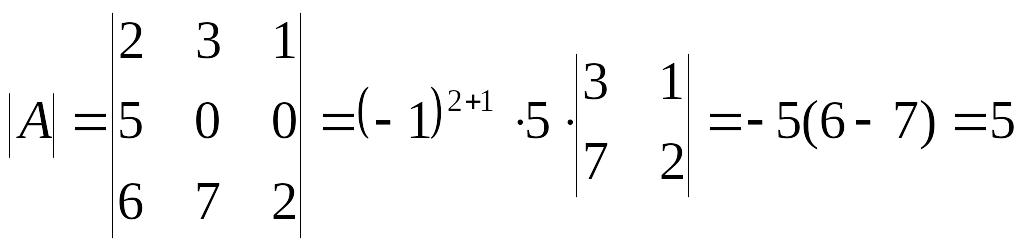