5.7. Ортогональные преобразования

Рассмотрим свойства матрицы перехода от одного ортонормированного базиса к другому ортонормированному базису в пространстве Е_n. Введем понятие ортогональной матрицы.

Определение. Матрица Т с вещественными элементами называется ортогональной, если т.е. .

Из определения следует, что ортогональная матрица всегда невырожденная, так как и , то .

Основные свойства ортогональной матрицы.

1. Матрица, обратная ортогональной, также ортогональна.

Пусть Т – ортогональная матрица, т.е. . Тогда , т.е. . Значит, матрица – ортогональна.

2. Матрица ортогональна тогда и только тогда, когда ее элементы удовлетворяют равенствам

.

Линейное преобразование Y=ТХ с ортогональной матрицей Т называется ортогональным. Так как , то ортогональное преобразование всегда невырожденное.

Теорема. Ортогональное преобразование координат не изменяет скалярного произведения векторов.

Доказательство. Рассмотрим линейный оператор , соответствующий матрице Т, и два произвольных вектора и из Е_n. Их образы обозначим через и , т.е. , . Тогда .

Поэтому .

Следствие 1. Ортогональное преобразование не меняет норм векторов и углов между векторами.

Следствие 2. Ортогональное преобразование переводит ортонормированный базис в ортонормированный.

Следствие 3. Матрица Т перехода от одного ортонормированного базиса к другому ортонормированному базису является ортогональной.

Следствие 4. Матрица Т, приводящая симметричную матрицу А к диагональному виду, является ортогональной.

5.8. Выпуклые множества

Рассмотрим совместную систему линейных уравнений

(5.8.1)

у которой ранг r матрицы меньше n , и пусть k=n-r.

Определение. Множество точек из Е_n, координаты которых удовлетворяют системе уравнений (5.8.1), называется k-мерной плоскостью. Одномерные плоскости называются прямыми, а (n-1)-мерные плоскости – гиперплоскостями.

Очевидно, что каждую гиперплоскость можно задать всего одним линейным уравнением:

.

В трехмерном пространстве Е₃ гиперплоскости – это обычные плоскости, а в Е₂ – это прямые.

Определение. Отрезком в Е_n, соединяющим точки , называется множество таких точек , что

Точки называются концами отрезка .

Определение. Множество Х пространства Е_n называется выпуклым, если вместе с любыми двумя точками ему принадлежит и соединяющих их отрезок .

Выпуклость множества Х означает, что из следует для всех . Например, в Е₂ выпуклый отрезок, полупрямая, круг, треугольник, полуплоскость и вся плоскость.

Определение. Множество Х точек пространства Е_n называется ограниченным, если координаты всех его точек в некотором базисе ограничены.

Пусть в пространстве задана гиперплоскость . Все точки из Е_n разбиваются этой гиперплоскостью на два полупространства: Х₁ – множество точек, для которых и – множество точек, для которых .

Теорема. Каждое полупространство пространства Е_n является выпуклым множеством.

Доказательство. Пусть точки и из Е_n принадлежат, например, полупространству Х₁. Тогда

Если – произвольная точка отрезка , то

Для этой точки имеем:

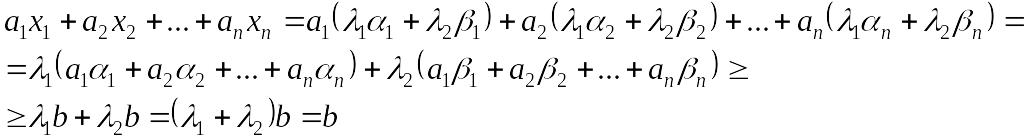
т.е. произвольная точка отрезка принадлежит Х₁. Теорема доказана.

Теорема. Пересечение любого числа выпуклых множеств есть множество выпуклое.

Доказательство. Пусть – выпуклые множества в Е_n. Если состоит из одной точки, то оно выпукло. Если более чем из одной, то пусть – любые две из них. Тогда и, так как все множества выпуклы, то и, следовательно, , что и требовалось доказать.

Из данной теоремы следует, что гиперплоскость как пересечение выпуклых множеств Х₁ и Х₂, является выпуклым множеством. Каждая k-мерная плоскость в Е_n также выпукла.

Пусть в Е_n даны m полупространств, определяемых неравенствами

.

(5.8.2)

Пересечение этих полупространств, называемое выпуклой многогранной областью, определяет множество решений системы линейных неравенств (5.8.2). Если это пересечение ограничено, оно называется выпуклым многогранником в Е_n.

Определение. Последовательность точек в Е_n сходится к точке при , если

.

Множество называется окрестностью точки .

Определение. Множество называется замкнутым, если оно содержит все свои предельные точки.

Определение. Точка из Е_n называется внутренней точкой множества Х, если существует такая ее -окрестность, все точки которой принадлежат множеству Х.

Определение. Точка из Е_n называется граничной точкой множества Х, если любая ее -окрестность содержит как точки, принадлежащие множеству Х, так и точки, ему не принадлежащие. Множество, состоящее из всех граничных точек множества Х, называется границей множества Х.

Определение. Точка называется крайней точкой (вершиной), если в Х не существует точек , что .

Для круга любая точка ограничивающей его окружности является крайней. Крайними точками являются все вершины выпуклого многогранника.

Определение. Точка называется выпуклой комбинацией точек , если существуют такие числа , что при условии .

Например, любая внутренняя точка круга является выпуклой комбинацией концов хорды, проходящей через эту точку.

Теорема (о представлении). Любая точка выпуклого замкнутого, ограниченного множества может быть представлена в виде выпуклой комбинации конечного числа крайних точек этого множества.

Пример. Используя теорему о представлении, выразить точку в виде выпуклой комбинации крайних точек множества , заданного системой неравенств

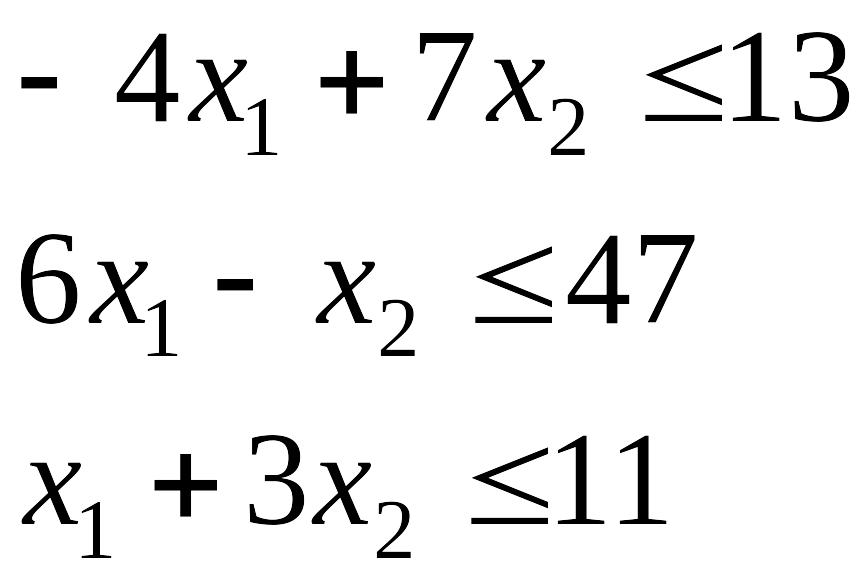
Р ешение. Очевидно, что множество Х выпукло. Множество Х (рис.5.1)

представляет собой треугольник с вершинами . На основании теоремы о представлении точку можно представить в виде следующей выпуклой комбинации:

.

В координатной форме получим два уравнения:

Добавляя к данной системе условие , получим систему трех линейных уравнений с тремя неизвестными. Решая систему методом Жордана-Гаусса, получаем

,

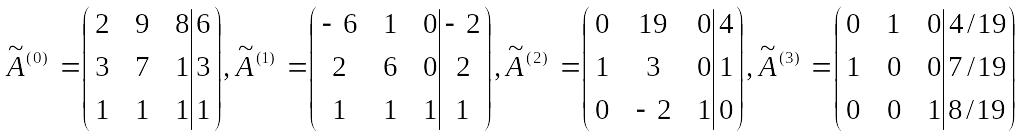откуда

Все эти коэффициенты удовлетворяют условию неотрицательности: . Поэтому искомое представление имеет вид .