2) Барометрическая формула.

Распределение молекул в поле силы тяжести является неравномерным. В жидкостях давление на различных глубинах различно в следствии гидростатического давления.

Для газов это соотношение может быть записано только для малых толщин:

т.о. т.о.

- барометрическая формула. Вывод получен при условии, что температура на всех высотах одинакова.

Распределение Больцмана.

Распределение Больцмана – распределение частиц в потенциальном поле. Барометрическая формула является частным случаем распределения частиц в потенциальном поле. Преобразуем его используя уравнение Менделеева-Клапейрона в виде: p=nkT

-распределение Больцмана.

Анализ:

1)T ∞, следовательно W_П/kT 0, n=n₀

2)T 0, след. W_П/kT ∞, n 0, Все молекулы падают на землю.

Билет 73

1. Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения

2. Уравнение плоской гармонической волны

Уравнением волны называется выражение, которое определяет смещение колеблющейся частицы как функцию координат и времени.

Найдем вид уравнения для плоской гармонической волны.

Пусть в начале координат находится источник плоских волн, которые распространяются вдоль оси x. Смещение точек среды в плоскости x = 0 совершается по гармоническому закону:

.

Найдем вид функции, описывающий колебания точек в некоторой плоскости x. Для того, чтобы волна прошла путь от источника до точки наблюдения, требуется время  , где v - фазовая скорость распространения волны (рис. 3.5).

Рис.3.5

Поэтому уравнение колебаний частиц, лежащих в плоскости x, будет иметь вид

Приведем это уравнение к симметричному виду:

.

Найдем, чему равно отношение , используя формулы (3.3), (3.20) и (3.22):

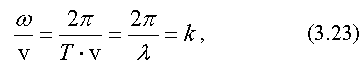
где k - волновое число.

Тогда получим уравнение плоской волны:

где A - амплитуда волны,        - фаза волны, т. е. фаза колебаний в точке с координатой x.

Формула (3.18) показывает, что смещение ξ   зависит от времени t и координаты x - координаты положения равновесия колеблющейся частицы среды.

Рис.3.6

На рис. 3.6 представлен график зависимости смещения от координаты при t = const (формула (3.24)). На этом рисунке показаны амплитуда волны A и длина волны  λ.

Фазовая и групповая скорость волны

Есть две важные характеристики волны с определенным законом дисперсии: фазовая скорость и групповая скорость.

Фазовая скорость — скорость движения поверхности постоянной фазы: . Направим осьx вдоль вектора . Тогда уравнение, определяющее поверхность постоянной фазы примет вид:kx–ω t = const, откуда , т. е. поверхность постоянной фазы движется со скоростьюω/k:

(16)

Направление фазовой скорости совпадает с направлением волнового вектора.

Для фотона и акустического фонона v_ph = c: фазовая скорость не зависит от волнового вектора.

Для электрона:

(17)

Групповая скорость — это скорость движения волнового пакета, составленного из гармонических волн с волновыми векторами лежащими вблизи заданного вектора (''группы'' волн):

(18)

Здесь интегрирование производится по небольшому объему обратного пространства Δ³ k: волновые вектора и частоты волн, составляющих волновой пакет, не слишком сильно отличаются от величин и— ''центральных'' волнового вектора и частоты пакета.

Т. к. отклонения отневелики, мы можем разложить функциюв ряд по величинес точностью до первого (линейного) члена:

(19)

Здесь — градиент частоты в точке.

Подставляя это разложение в интеграл, определяющий волновой пакет, получим:

(20)

(21)

Видно, что зависимость амплитуды волнового пакета |f| от координат и времени сводится к зависимости только от величины . Иными словами, пакет движется как целое со скоростью. Это и есть групповая скоростьv_g:

(22)

Заметим, что мы учли лишь линейный член в разложении в окрестности, в этом приближении огибающая (форма) волнового пакета сохраняет свою форму. На самом же деле, если дисперсия не линейная, пакет медленно расплывается.

Если частота (энергия квазичастицы) зависит только от модуля волнового вектора, то групповая скорость направлена вдоль и по абсолютной величине равна ∂ω/∂ k.

Для свободного электрона получаем: v_g = ħ k/m = p/m. Как и следовало ожидать, групповая скорость совпадает с классической скоростью электрона.

У волн с линейной дисперсией (фотонов и акустических фононов) групповая скорость равна фазовой. Поэтому одномерный волновой пакет из из таких волн не расплывается, т. е. сохраняет свою форму.

Волновой вектор — вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу

Волново́е число́ - это величина, обратная длине волны, т. е. это число волн на отрезке 2π. Единица измерения — обратная длина, точнее рад . м^-1. Обозначение - k, формула:

где:

- λ -  длина волны,

- ν (греческая буква «ню»)  -  частота,

- v_p  -  Фазовая скорость волны,

- ω  -  угловая частота,

- E  -  энергия,

- ħ  -  редуцированная постоянная Планка, (постоянная Дирака)

- c  -  скорость света в вакууме

В спектроскопии волновое число измеряют в обратных сантиметрах (см^-1).

Билет 74

1. Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по закону синуса или косинуса. Графически гармонические колебания изображаются кривой — синусоидой или косинусоидой; они могут быть записаны в форме: или, где х — значение колеблющейся величины в данный момент времени t (для механических Г. к., например, смещение или скорость, для электрических гармонических колебаний — напряжение или сила тока), А — амплитуда колебаний, w — угловая частота колебаний,— фаза колебаний,— начальная фаза колебаний.

Гармонические колебания занимают среди всех разнообразных форм колебаний важное место, оно определяется двумя обстоятельствами. Во-первых, в природе и в технике очень часто встречаются колебательные процессы, по форме близкие к гармоническим колебаниям. Во-вторых, очень широкий класс систем, свойства которых можно считать неизменными (например, электрические цепи, у которых индуктивность, ёмкость и сопротивление не зависят от напряжения и силы тока в цепи), по отношению к гармоническим колебаниям ведут себя особым образом: при воздействии на них гармонических колебаний совершаемые ими вынужденные колебания имеют также форму гармонических колебаний (когда форма внешнего воздействия отличается от гармонических колебаний, форма вынужденного колебания системы всегда отличается от формы внешнего воздействия). Иначе говоря, в большинстве случаев гармонические колебания единственный тип колебаний, форма которых не искажается при воспроизведении; это и определяет особое значение гармонических колебаний, а также возможность представления негармонических колебаний в виде гармонического спектра колебаний

Дифференциальное уравнение, описывающее вынужденные колебания

наших двух систем будет иметь один и тот же вид:

.

 

14.5.6. Решение дифференциального уравнения

Решение дифференциального уравнения вынужденных колебаний - ξ(t) - состоит из двух слагаемых:

,

здесь ξ₁(t) - общее решение однородного уравнения, т.е. уравнения с нулем в правой части (см. 14.4.5.),

ξ₂(t) - частное решение неоднородного уравнения, т.е. уравнения с ненулевой правой частью - (14.5.5)

- из (14.4.6),

здесь -    - частота затухающих колебаний.

ξ₁(t) убывает с течением времени и его роль существенна при переходных процессах. Стационарное, установившееся значение ξ(t) определяется, в основном, слагаемым ξ₂(t). Наша задача - найти ξ₂(t).

14.5.6.1. Частное решение неоднородного уравнения

Частное решение неоднородного уравнения - ξ₂(t). Ищем ξ₂(t) в виде гармонической функции изменяющейся с частотой внешнего воздействия ω :

.

Первая и вторая производные от этой функции также будут гармоническими функциями, изменяющиеся с частотой ω. Значит, в уравнении 14.5.3.5, в левой его части, будет сумма трех гармонических функций одинаковой частоты, справа - гармоническая функция той же частоты, т.е. сумма трех колебаний одной частоты равна четвертому колебанию той же частоты. Задачу о сложении колебаний мы решим методом векторных диаграмм (14.3.1.), для этого и , после нахождения этих производных, запишем с помощью функции косинуса:

2.Атмосферное давление уменьшается по мере увеличения высоты, поскольку оно создаётся лишь вышележащим слоем атмосферы. Зависимость давления от высоты описывается т. н. барометрической формулой

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), Б. ф. имеет следующий вид:

,

где p — давление газа в слое, расположенном на высоте h, p₀ — давление на нулевом уровне (h = h₀), m — молекулярная масса газа, R — газовая постоянная, T — абсолютная температура. Из Б. ф. следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:

,

где m — масса молекулы, k — постоянная Больцмана.

Б. ф. может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Больцмана статистика). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 применил Б. ф. к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.

Б. ф. показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина , определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональнойkT. Чем выше температура T, тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести mg (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести mg может изменяться за счёт двух величин: ускорения g и массы частиц m.

Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.

Реальное распределение давления и плотности воздуха в земной атмосфере не следует Б. ф., т.к. в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.

Б. ф. лежит в основе барометрического нивелирования — метода определения разности высот Δh между двумя точками по измеряемому в этих точках давлению (p₁ и p₂). Поскольку атмосферное давление зависит от погоды, интервал времени между измерениями должен быть возможно меньшим, а пункты измерения располагаться не слишком далеко друг от друга. Б. ф. записывается в этом случае в виде: Δh = 18400(1 + at)lg(p₁ / p₂) (в м), где t — средняя температура слоя воздуха между точками измерения, a — температурный коэффициент объёмного расширения воздуха. Погрешность при расчётах по этой формуле не превышает 0,1-0,5% от измеряемой высоты. Более точна формула Лапласа, учитывающая влияние влажности воздуха и изменение ускорения свободного падения.

Билет 75

1. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянно убывающей со временем амплитудой.

        Свободные колебания реальных систем всегда затухают. Затухание обусловлено в основном трением (механические системы) и сопротивлением ( в электромагнитных колебательных контурах).

        Колебательная система называется линейной, если её свойства не меняются при колебаниях, то есть такие параметры, как сила тяжести, упругость пружины, сопротивление, емкость, индуктивность не зависят ни от смещения, ни от скорости, ни от ускорения колеблющейся величины. В дальнейшем мы будем рассматривать только линейные системы.

Дифференциальное уравнение свободных затухающих колебание линейной системы имеет вид: d²x/dt²+2dx/dt+₀²x=0. Здесь x- изменяющаяся при колебаниях физическая характеристика системы, =const>0 – коэффициент затухания, а ₀- циклическая частота свободных незатухающих колебаний той же системы, т.е. в отсутствие потерь энергии(при =0). Решением этого уравнения затухающих колебаний имеет вид: x=A₀e^-tcos(t+£). Здесь =₀²-²), а постоянные величины А₀ и £ зависят от начальных условий, т.е. от значений x и dx/dt в начальный момент времени (t=0). Затухающие колебания не являются периодическими. Например, максимальное значение колеблющейся величины x, достигаемое в некоторый момент времени t₁, в последующем (при t>t₁) никогда не повторяется. Однако при затухающих колебаниях величина x обращается в 0, изменяясь в одну и ту же сторону, а так же достигает максимальное и минимальное значения через равные промежутки времени: T=2П/=2п/₀²-²). Поэтому величины T и  условно называют периодом (условным периодом) и циклической частотой (условной циклической частотой) затухающих колебаний. Величина А=А₀е^-t называется амплитудой затухающих колебаний, соответственно А₀- начальной амплитудой. Промежуток времени =1/, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

2. Закон Больцмана для распределения частиц идеального газа во внешнем потенциальном поле. n=n₀exp(-_p/(kT)) Больцман доказал, что это распределение справедливо не только в случае потенциальных сил земного тяготения, но и в любом потенциальном поле сил совокупности любых одинаковых частиц, находящихся в состоянии хаотического движения. В соответствии с этим это распределение было названо законом Больцмана для распределения частиц идеального газа во внешнем потенциальном поле.

Распределения Больцмана. Основное уравнение МКТ и максвелские распределения молекул по скорости были получены предположением, что молекулы равномерно распределены по объему и все направления движения молекул равномерно распределены по объему и все направления движения молекул равновероятны. Такие условия могут быть реализованы только в том случае, если на молекулы не действуют никакие внешние силовые поля. Однако молекулы любого газа в земных условиях находятся в потенциальном гравитационном поле Земли, что приводит к нарушению равномерного распределения молекул по объему. P = pgh – давление в жидкости ; dP = - pgdh – т.к. с увеличением высоты давление уменьшается.

PV = mRT / μ => p = m / V = Pμ / RT ; dP = - Pμ g dh / RT = P m0 g dh / kT ; dP/ P = - m0 g dh / kT ; Проинтегрируем это выражение:

(интеграл P0 - P) dP / P = - (m0 g / kT) (интеграл 0 - h) dh ; ln (P / P0) = - (m0 gh / kT) ; P = R0 e (ст. m0 gh / kT) ; P = P0 e (ст. – μ n / RT) ; Это выражение описывает распределение частиц по высоте в гравитационном поле. m0 gh = Wп, поэтому n = n0 e (ст. – Wп / kT). Это и есть распределения Больцмана. Оно описывает распределение частиц по высоте в гравитационном поле, а не только в гравитационном поле Земли. Это распределение приемлемо к частицам, находящимся в состоянии заотического теплового движения.

Билет 76

1. Вращательный момент. Моментом силы M называется величина M=r *F

(* - скалярное произведение, все значения векторные) r – радиус-вектор, F – сила ; r *sinАЛЬФА = l ; M = r F sinАЛЬФА = r sinАЛЬФА F = F l

(рисунок – вектор M вверх; вектор r чуть выше места, где по идее должна быть ось OX; на 90 градусов от r от M проходит из той же точки прямая L ; векотор F скрещивается с r под углом АЛЬФА).

ПЛЕЧО СИЛЫ - кратчайшее росстояние от данной точки (центра) до линии действия силы. См. Момент силы.

Основное уравнение динамики вращательного движения. Wk = 1/2 J * w(ст.2) ; dWk = 1/2 J 2w dw = Jwdw ; dWk = dA ; M dФИ = Jwdw;

M dФИ/dt = Jw dw/dt ; w = dФИ/dt ; E = dw/dt ; M w = J w E ; M = J E (M,E - вектора). Основное уравнение динамики вращательного движения. Это аналог 2го закона Ньютона для вращательного движения. (F-M, m-J, a-E).

2. Вывод волнового уравнения из .

Пусть волна распространяется вдоль упругого стержня. Рассмотрим элемент этого стержня, его длина равна Δx в невозмущенном состоянии. Пусть при распространения волны левая часть этого элемента сместится на величину ξ(x), а правая - на величину ξ(x + Δx), не равную смещению левой части.

.

В нашем примере стержень растянут внешними силами:

Сумма этих сил равна:

.

Домножим и поделим последнее выражение на Δ x. Величина

при Δx → 0 дает вторую производную от "кси" по x, т.е. .

Тогда .

Масса нашего элемента , его ускорение (3.10)

,

тогда преобразуется в

,

или

- волновое уравнение.

Проверим, будет ли его решением.

Откуда

.

Т.к. (15.2.4), то фазовая скорость упругой продольной волны:

,

и волновое уравнение можно записать в виде:

.

Для волны, распространяющейся в произвольном направлении (15.2.5) волновое уравнение имеет вид:

.

Волновое уравнение

Применяя второй закон Ньютона (4.6) к упругой среде, можно получить дифференциальное уравнение в частных производных, решением которого будет уравнение волны. Логическая схема этого вывода такова:

Уравнение плоской волны.

Пусть в начале координат находится твердая плоскость, которая колеблется по гармоническому закону и вынуждает частицы упругой среды, находящейся рядом с ней, колебаться по этому же закону. Направим ось x перпендикулярно этой плоскости. Тогда вдоль этой оси будет распространяться плоская гармоническая продольная волна. Наша задача - найти - уравнение волны, если задано .

Колебания до волновой поверхности, удаленной от начала координат на расстояние x, дойдут через время , значит уравнение волны

.

Длина́ волны́ — расстояние между двумя ближайшими точками волны, находящимися в одинаковой фазе колебания. Одна из основных характеристик колебаний. Измеряется в единицах расстояния (метры, сантиметры и т.п.). Величина обратная длине волны называется волновым числом.

Чаще всего длина влоны обозначается греческой буквой λ.

Соотношения между другими параметрами волны: со скоростью волны (v) и частотой(f)

X = 2ПИ / λ – ВОЛНОВОЕ ЧИСЛО (волновой вектор) – вектор, направление которого совпадает с направлением движения волны.

Билет 77

1. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянно убывающей со временем амплитудой.

        Свободные колебания реальных систем всегда затухают. Затухание обусловлено в основном трением (механические системы) и сопротивлением ( в электромагнитных колебательных контурах).

        Колебательная система называется линейной, если её свойства не меняются при колебаниях, то есть такие параметры, как сила тяжести, упругость пружины, сопротивление, емкость, индуктивность не зависят ни от смещения, ни от скорости, ни от ускорения колеблющейся величины. В дальнейшем мы будем рассматривать только линейные системы.

Дифференциальное уравнение, описывающее затухающие колебания наших двух систем в этих обозначениях будет иметь один и тот же вид

.

14.4.6. Решение

Каким будет его решение? При    (отсутствие сопротивления, трения) оно должно переходить в    (см. 14.2).

Наличие затухания, потерь энергии, переход ее из электромагнитной или механической в тепловую приведет к уменьшению амплитуды колебаний с течением времени, станет другой, меньшей чем ω₀, и частота колебаний.

Предположим, что амплитуда убывает по экспоненциальному закону, т.е. A(t) = A₀·e^-βt(e=2,71828...),

тогда решение будем искать в виде:

Логарифмический декремент затухания

,

подставим A(t) = A₀^-βt.

Частота затухающих колебаний

2. Внутренняя энергия идеального газа равна суммарной кинетической энергии всех молекул, составляющих систему (напомним, что потенциальной энергией взаимодействия молекул идеального газа пренебрегают),

,

где - средняя кинетическая энергия одной молекулы, N - число молекул в системе, которое может быть найдено из формулы (4.2).

,

где m - масса газа, μ - молярная масса, N_A - число Авогадро.

Следовательно, внутренняя энергия идеального газа равна

.

Учтем, что - газовая постоянная. Тогда внутренняя энергия идеального газа равна

Изменение внутренней энергии зависит от изменения температуры, т. е.

В дифференциальной форме эта формула запишется следующим образом

Внутренняя энергия системы может измениться за счет двух различных процессов: совершения над системой работы A^/ и сообщения количества теплоты . Заметим, что работа, совершаемая над системой внешними силами, и работа, совершаемая системой против внешних сил, равны по величине и противоположны по знаку (см. пояснение к формуле (1.25)): A^/ = - A.

Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема (закон Джоуля).

Изменяется ли внутренняя энергия воздуха в открытом сосуде при его нагревании ДА ИЗМЕНЯЕТЬСЯ

Билет 78

2. Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что невозможно всю внутреннюю энергию тела превратить в полезную работу.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения

Термодинамическая энтропия — аддитивная термодинамическая величина, функция состояния термодинамической системы

ПРИНЦИП ВОЗРАСТАНИЯ ЭНТРОПИИ сводится к утверждению, что энтропия изолированных систем неизменно возрастает при всяком изменении их состояния и остается постоянной лишь при обратимом течении процессов: Оба вывода о существовании и возрастании энтропии получаются на основе какого-либо постулата, отражающего необратимость реальных процессов в природе. Наиболее часто в доказательстве объединенного принципа существования и возрастания энтропии используют постулаты Р.Клаузиуса, В.Томпсона-Кельвина, М. Планка. В действительности принципы существования и возрастания энтропии ничего общего не имеют. Физическое содержание: принцип существования энтропии характеризует термодинамические свойства систем, а принцип возрастания энтропии - наиболее вероятное течение реальных процессов. Математическое выражение принципа существования энтропии - равенство, а принципа возрастания - неравенство. Области применения: принцип существования энтропии и вытекающие из него следствия используют для изучения физических свойств веществ, а принцип возрастания энтропии - для суждения о наиболее вероятном течении физических явлений. Философское значение этих принципов также различно. В связи с этим принципы существования и возрастания энтропии рассматриваются раздельно и математические выражения их для любых тел получаются на базе различных постулатов. Вывод о существовании абсолютной температуры T и энтропии s как термодинамических функций состояния любых тел и систем составляет основное содержание второго закона термодинамики и распространяется на любые процессы - обратимые и необратимые.

Вероятность Термодинамическая - число, пропорциональное количествуфизически различимых микроскопических состояний, которыми может бытьреализовано данное макроскопическое состояние системы. Напр., состояниегаза с определенной энергией может быть реализовано множеством способов,различающихся распределением энергии между частицами.

Билет 79

1. ПЛЕЧО СИЛЫ - кратчайшее росстояние от данной точки (центра) до линии действия силы

Уравнение динамики вращательного движения Из (5.5):

.

Используем (7.1) и (7.2):

.

Используем (6.3):

,

Откуда

.

Получим основное уравнение динамики вращательного движения, сравнить с (4.6):

2. Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД и нулевой мощностью.

Цикл Карно назван в честь фразцузского физика Сади Карно, который впервые его исследовал.

Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется.

Мощность тепловой машины Карно

Передача тепла от нагревателя рабочему телу и от рабочего тела холодильнику происходит в цикле Карно в отсутствии разности температур. Благодаря этому цикл Карно обратим (передача тепла при наличии конечной разности температур всегда необратима согласно постулату Томсона). Но при отсутствии разности температур тепло передается бесконечно медленно. Поэтому мощность тепловой машины Карно равна нулю

Билет 80

1. Механическая работа – выражение, определяемое соотношением:

A=FScos = FS

Формула может быть использована только тогда, когда F-const, a перемещение прямолинейно. Если перемещение не прямолинейно, а F-не const, то траекторию разбивают и считают что на S перемещение прямолинейно, а F-const

Примеры работы сил:

1) Работа сил упругости

2) Работа сил тяжести

dA=mgdh= mgdrcos=mgdh,

Работа сил тяжести не зависит от траектории, а определяется уровнем над поверхностью земли. Силы, работа которых не зависит от траектории, а определяется только начальным и конечным положением наз. консервативные силами (Сила тяжести, Гравитационная, Электростатическая, ). Если F=const, -мощность.