1. Затухающие гармонические колебания. Их дифференциальное уравнение и его решение. Логарифмический декремент затухания и добротность колебательной системы.

Затухающие колебания. Колебания с течением времени затухают. Это связано с тем, что действуют силы сопротивления, которые при малых скоростях пропорциональны скорости.

Таким образом, 2-й закон Ньютона записывается в виде:

Полученное дифференциальное уравнение называется дифференциальным уравнением затухающих колебаний.

Решением является функция:

ω₀ – частота свободных колебаний

 – коэффициент затухания.

При больших возможно, что =0: Апериодический процесс. В этом случае, энергия, полученная от отклонения, полностью расходуется на преодоление сил сопротивления.

Характеризуется логарифмическим декрементом:

Добротноть. Для характеристики осциллирующей системы часто принимается величина Q называемая добротностью. Эта величина представляет собой умноженное на 2 отношение запасённой энергии к среднему значению энергии, теряемому за один период. Большим значениям Q соответствует слабое затухание осциллятора.Q=/ , где  логарифмический декремент затухания.

2. Изопроцессы идеального газа и газовые законы.

1) V = const изохорный => dV=0 ; d = PdV=0 ; dQ=dU ; dU = МЮ dUмол = МЮ Cv dT ;

dQ= МЮ Cv dT ; Q = (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T2 – T1) – m Cv (T2 – T1)/ μ

2) T = const изотермический => dT= 0 ; dQ= МЮ Cv dT = 0 ; dQ = dA ;

dA = PdV ; PV = МЮ RT ; P= МЮ RT / V ; dA = МЮ RT dV / V ;

A = (интеграл V1 – V2) МЮ RTdV / V = МЮ RT (интеграл V1 – V2) dV/ V = МЮ RT ln (V2/ V1) = МЮ RT ln (P1/ P2) ; P1 V1 = P2 V2 ;

3) P = const изобарический => dQ = PdV ; A = (интеграл V1 – V2) PdV = P (V2 – V1) ; A = P (V2 – V1) ; dU = МЮ Cv dT ; PdV = МЮ RdT ; dQ = МЮ Cv dT + МЮ Rdt = МЮ (Cv + R) dT ; Q = МЮ Cp (T2 – T1) ;

4) Q = const Адиабатный dA = dU ; dA = МЮ Cv dT ; PdV = - МЮ Cv dT ; PV = МЮ RT – продифференцированное уравнение Менделеева-Клайперона ; PdV + VdP = МЮ R dT ; … ; lnP = - γ lnP + const ; γ – коэффициент Пуассона ; lnP + lnV (ст. γ) = const ; PV (ст. γ) = const ; (график такой же как и изотермический, только чуть выше вверх).

dA = - dU = - МЮ Cv dT ; A = - (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T1 – T2) ;

Билет 55

1. Колебательное движение. Период, частота, амплитуда и фаза колебания. Гармоническое колебание, его векторное и комплексное представление.

Колебания – любой периодический процесс, при этом все характеристики колебаний являются периодическими функциями. Период – время, за которое процесс возвращается в исходное состояние. Частота – кол-во колебаний за сек. Простейший вид колебаний – гармонические колебания. Это колебания, происходящие по закону sin или cos. Кинематическим уравнением гармонических колебаний является функция:

X – смещение частицы относительно положения равновесия в мом. времени t.

A – амплитуда колебаний (Максимальное смещение).

t+₀ – фаза колебаний.

₀ – начальная фаза.

векторное представление x=Acosφ φ=ωt+φ₀ X=Acos(ωt+φ₀)

Комплексное представления гармонических колебаний.

Любое действительное число может быть представлено точкой на числовой оси.

Комплексное число Z=x+iy

2. Явления переноса. Молекулярно-кинетическая теория вязкости.

Явление переноса в газах.

Постоянное тепловое хаотическое движение приводит к непрерывному перемещению молекул. При этом если в газе возникают какая либо неоднородность то со временем все неоднородности выравниваются. Эти процессы выравнивания не являются хаотическими, а характеризуются определенной направленностью. Это связано с перемещением характеристик газа от областей с избытком к областям с недостатком. Существует 3 типа неоднородностей:

1)Неоднородность плотности (концентрации);

2)Неоднородность температуры (энергии);

3)Неоднородность импульса (перемещения) отдельных слоев движения газа;

Вязкость - Явление вязкости связано с возникновением сил трения между слоями жидкости или газа, которые перемещаются параллельно друг другу, но с разными скоростями

Вязкость или внутреннее трение. В потоке газа молекулы участвуют одновременно в двух видах движений – хаотическом тепловом и упорядоченном направленном движении. Пусть <v> - скорость хаотического теплового движения, а <u> - скорость упорядоченного движения молекул ; u значительно меньше v ; В результате движения молекул, молекулы из слоя газа, двигающегося с одной поступательной скоростью u будут перемешиваться с молекулами из другого слоя. В результате столкновеня молекул между собой молекулы из быстрого слоя будут передавать часть своего импульса молекулам из медленного слоя и таким образом тормозиться. По этой причине в газе возникает своеобразная сила внутреннего трения, которая замедляет движение быстрых слоев и ускоряет движение медленных слоев.

Билет 56

1. Незатухающие гармонические колебания и их дифференциальное уравнение. Математический и пружинный маятники и вывод формул для расчета периодов их незатухающих колебаний. Энергия гармонического осциллятора.

Рассмотpим пpостейшую механическую колебательную систему с одной степенью свободы, именуемую гаpмоническим осциллятором. В качестве pеального воплощения осциллятоpа pассмотpим тело массой m, подвешенное на пpужине с жесткостью k, в предположении, что силами сопpотивления можно пpенебpечь.

Если твердое тело представляет собой материальную точку, подвешенную на невесомой, нерастяжимой нити и способную совершать колебания, то маятник будет математическом. J = md² ; T = 2π√ md²/ mgd = 2 π√d / g; T = 2π √d / g – период колебания математического маятника. Пружинный маятник. Рассмотрим колебания груза на пружине:

F_упр = - kx (закон Гука); ma = F_упр ; m * (d2 x / dt (ст.2)) = - kx ;

(d² x / dt ) + kx / m = 0 – это дифференциальное уравнение, описывающее колебания груза на пружине, жесткость которого равна k.

Частота этих колебаний: w₀ = √ k / m ;

Период: T=2 π√m / k

Кинетическая энергия гармонических колебаний.

Среднее значение энергии:

2. Число степеней свободы молекул. Закон равнораспределения энергии теплового движения молекул. Внутренняя энергия идеального газа.

Закон равномерного распределения энергии по степеням свободы.

Числом степеней свободы называют количество независимых координат, которые определяют положение тела в пространстве. Точка в пространстве имеет 3 координаты и имеет 3 степени свободы. Твердое тело имеет 3 степени свободы, центра инерции и 3 вращательных степени свободы. Молекулы идеального газа имеют среднюю кинетическую энергию . Таким образом, на одну степень свободы приходитсяkT/2. Этот закон очевиден для идеального газа и справедлив для любого случая и гласит, что на одну степень свободы в среднем приходится одинаковое количество энергии равное kT/2.

1. i 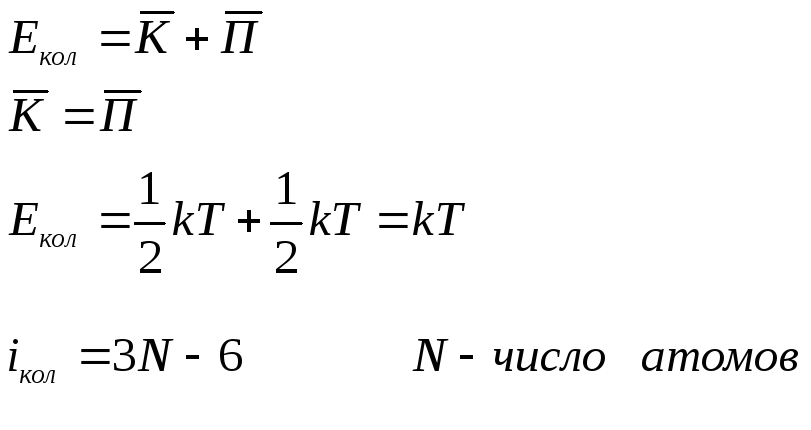=3 – одноатомный

2. i =3+2=5 – 2-х атомный

3. i=3+3=6 – 3-х атомный и более

Для многоатомного газа:

Внутренняя энергия идеального газа.

Внутренняя энергия идеального газа состоит из учета потенциальной энергии и кинетической энергии движения атомов или молекул, поэтому величина внутренней энергии определяются выражением:

Внутренняя энергия – это функция состояние газа. Она прямо пропорциональна абсолютной температуре и характеризует энергию всех молекул газа.

Билет 57

1. Угловая скорость и угловое ускорение при вращательном движении. Их связь с мгновенной скоростью и мгновенным нормальным и тангенциальным ускорениями.

Вращательное - движение, когда все точки тела движутся по концентрическим окружностям, центры которых лежат на одной прямой, которая называется осью вращения.

ω - угловая скорость, характеризующая быстроту углового перемещен

–средняя скорость

–мгновенная скорость

- равномерное угловое вращение; [ω] = Рад/сек.

–линейная скорость вращения

- угловое ускорение, характеризует быстроту изменения угловой скорости.

;

Связь между характеристикой поступательного и вращательного движения

Если-const, то угловой путь и угловая скорость определяется

‘+’-равноускоренное движение

Векторное представление угловых характеристик.

a) Ускоренное вращение

>0

>0

б) Замедленное вращение

υ=[ωr]; υ=[ωR]

υ=ωrsinθ

2. Распределение Максвелла молекул по скоростям и энергиям теплового движения. Средняя, среднеквадратичная и наиболее вероятная скорости движения молекул и соотношение между ними.

Введенная ранее средняя квадратичная скорость характеризует среднюю интенсивность движения, ясно, что при хаотическом движении молекулы движутся с различными скоростями. Очевидно, что число молекул с очень маленькими скоростями, как и число молекул со скоростями сравнительно невелико. Основное количество молекул имеет скорости близкие к _КВ Распределение по скоростям установил Максвелл. Для этого он ввел функцию распределения f_(). Физический смысл этой функции заключается в том, что она позволяет вычислить число молекул dN движущихся со скоростями в интервале (,+d) dN = f_()d

В конечном интервале (1,2):

Графическая зависимость функции распределения от скорости имеет вид:

Аналитический вид:

(N–общее число молекул) (m₀ – масса одной молекулы)

-наиболее вероятная скорость

- средняя арифметическая скорость

- средняя квадратичная скорость.

При увеличении температуры интенсивность движения возрастает

Билет 58

1. Момент инерции твёрдого тела. Теорема Штейнера. Пользуясь этой теоремой, рассчитайте момент инерции шара массой m и радиусом R относительно оси, касательной к его поверхности.

- момент инерции твёрдого тела.

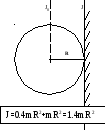Момент инерции характеризует меру инертности тела при вращательном движении. Его величина зависит от массы тела, а также от распределения массы относительно оси вращения каждое тело может иметь бесчисленное количество моментов инерции определяемых относительно разных осей вращения. Таким образом, получили основной закон динамики вращательного движения: Теорема Штейнера: Момент инерции тонкого стержня dJ=dmx² =m/ L – линейная плотность dm=dx dJ= x²dx

Моменты инерции тел: (МТ mR; Обруч mR²; Диск(цилиндр)1/2mR² ; Шар 2/5mR² ; Тонкий стержень J=1/12mL² ; Полый цилиндр J=1/2(R₁²+R₂²).

Если известен момент инерции относительно оси, проходящей через центр инерции J₀ , то момент инерции J относительно другой оси, параллельной первой, можно вычислить по формуле J=J₀ + md².

2. Плоская гармоническая волна. Бегущие и стоячие волны. Фазовая скорость, длина волны, волновое число.

Волновой фронт – это геометрическое место точек пространства, до которого дошли колебания к моменту времени t. Фаза колебания у всех этих точек имеет одно и то же значение.

Волновая поверхность – это геометрическое место точек в пространстве, фаза колебания которых одинакова.

Волновой фронт один, а волновых поверхностей бесчисленное множество. В зависимости от формы фронта или волновой поверхности волны делятся на плоские, сферические и т.д.

Стоячая волна энергии не переносит. Стоячие волны образуюся в результате интерференции (наложения) 2х одинаковых, противоположных по направлению волн. Энергия, переносимая волной количественно характеризуется вектором плотности потока энергии, вектором Умова.

y = A sin (wt + φ₀)

Колебания в точку, расположенную на расстоянии X от начала координат приходит с запозданием на время x/v и среднее колебание в точке, с координатами X будет описываться выражением:

y (x, t) = A sin [w (t – x/v) + φ₀] ; w (t – x/v) = wt – wx/v ; w = 2 π / T ; λ = vT  T = λ / v ; w = 2π v/ λ ;

Бегущие волны – волны переносящие энергию. Уравнение бегущей волны – функция, показывающая положение частиц от времени. S(x,t) S(t)=Acos(t)

В некотором направлении X, при скорости волны V, колебания точки на расстоянии x будут запаздывать на Δt. Поэтому смещение будет равно:

S(x,t)=Acos(ω(t–Δt))=Acos(ω(t–x/V))

Расстояние, которое проходит волна за один период, называют длинной волны.

Фазовая скорость – скорость передвижения фронта волны, зависит от плотности среды других свойств. E – модуль Юнга, ρ – плотность среды

Билет 59

1. Момент силы и момент импульса. Закон сохранения момента импульса.

Момент силы. 2-й закон Ньютона для вращательного движения.

Опыт показывает, что одна и та же сила оказывает разное вращательное действие.

M=FRsinα F_τ=Fsinα M=F_τR

Действие касательной силы на материальную точку может привести к движению с тангенсальным ускорением:

F_=ma_ a=R F_= mR F_R=mR² M=J

M=F_ R

J=mR² - момент инерции

–угловое ускорение

Момент импульса точки.

2-й закон Ньютона для вращательного движения (в другой форме).

- Момент импульса

- в импульсной форме. Действие момента силы равно скорости изменения момента импульса (Если M –const)

(при М -const) L=J=mR²=mR²/R=mR момент импульса и импульс точки связаны между собой

Момент импульса можно определить и относительно начала координат L=mrsin

Закон сохранения момента импульса.

Из основного закона динамики вращательного движения следует: если результирующий момент сил равен нулю, соответственно dL/dt=0, то означает суммарный момент импульса остаётся постоянным. Таким образом, если на систему не действуют ни ускорение, ни тормозящие моменты сил, то величина и направление момента импульса остаются постоянными.

J₁₁= J₂₂, если J₁ >J₂ ₂ >₁

L₁=L₂

2. Идеальный газ. Давление газа с точки зрения молекулярно-кинетической теории. Выведите основное уравнение молекулярно-кинетической теории идеального газа.

Идеальным газом называют газ, в котором отсутствуют взаимодействие между молекулами и размеры атомов пренебрежимо малы (материальные точки), атомы или молекулы совершают упругие соударения со стенками сосуда. При этих условиях молекулы идеального газа оказывают силовое воздействие на стенки сосуда, которое характеризуется физической величиной называемой давлением.P=F/S, Па. Давление – сила, действующая на единицу поверхности.

Основное уравнение МКТ.

Поскольку молекулы движутся хаотически, то на каждую стенку давление будет оказываться в 6 раз меньше.

Билет60

1. Вращательное движение тела. Взаимосвязь кинематических характеристик вращательного и поступательного движений.

Вращательное - движение, когда все точки тела движутся по концентрическим окружностям, центры которых лежат на одной прямой, которая называется осью вращения.

ω - угловая скорость, характеризующая быстроту углового перемещен

–средняя скорость – мгновенная скорость - равномерное угловое вращение; [ω] = Рад/сек.

–линейная скорость вращения,- угловое ускорение, характеризует быстроту изменения угловой скорости.;

Связь между характеристикой поступательного и вращательного движения

Если -const, то угловой путь и угловая скорость определяется

‘+’-равноускоренное движение

Векторное представление угловых характеристик.

a) Ускоренное вращение

>0

>0

б) Замедленное вращение

υ=[ωr]; υ=[ωR]

υ=ωrsinθ

2. Распределение Максвелла молекул по скоростям и энергиям теплового движения. Соотношение между средней, среднеквадратичной и наиболее вероятной скоростями.

Распределения Максвелла молекул по скоростям.

Введенная ранее средняя квадратичная скорость характеризует среднюю интенсивность движения, ясно, что при хаотическом движении молекулы движутся с различными скоростями. Очевидно, что число молекул с очень маленькими скоростями, как и число молекул со скоростями сравнительно невелико. Основное количество молекул имеет скорости близкие к _КВ Распределение по скоростям установил Максвелл. Для этого он ввел функцию распределения f_(). Физический смысл этой функции заключается в том, что она позволяет вычислить число молекул dN движущихся со скоростями в интервале (,+d) dN = f_()d

В конечном интервале (1,2):

Графическая зависимость функции распределения от скорости имеет вид:

Аналитический вид:

(N–общее число молекул) (m₀ – масса одной молекулы)

-наиболее вероятная скорость

- средняя арифметическая скорость

- средняя квадратичная скорость.

При увеличении температуры интенсивность движения возрастает

Билет 61.

1. Моментом импульса (моментом количества движения) матерьяльной точки относительно оси называется векторная величина L = r * P ; где все величины – векторы ; r – расстояние от оси вращения до этой точки. Импульс точки: P = mv. Моментом силы M называется величина M=r *F

Моментом импульса твердого тела относительно оси является

L = сумма ri Pi ; |L| = |r | |P| sinАЛЬФА ; Рассмотрим случай, когда АЛЬФА=ПИ/ 2: L = сумма mi vi ri = w сумма mi vi (ст.2) = J w; L = J w ;

Продефференцируем это выражение по времени: dL / dt = J dw/dt = J центромасс = M ; dL / dt = M ; Если M= 0, то dL / dt = 0  L = const

Это закон сохранения импульса!!! --- Если на систему тел не действует момент силы M или равнодействующая всех сил равна нулю, то момент импульса этой системы остается постоянным. Закон сохранения момента импульса является фундаментальным законом физики. Он справедлив не только в классической механике, но и в релитивистской и в квантовой механике. Закон сохранения момента импульса связан с изотропностью пространства – пространство обладает одинаковыми свойствами во всех направлениях.

2. Во всякой реальной колебательной системе всегда присутствует сила трения, которую также необходимо учитывать при рассмотрении колебания. При колебательном движении осциллятора им будет совершена работа против сил трения, в результате чего энергия колебаний будет постепенно уменьшаться и как следствие будет уменьшаться амплитуда колебаний. Свободные затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается из-за потерь энергии колебательной системой. Рассмотрим линейную колебательную систему – систему, параметры которой не изменяются в ходе колебаний. Рассмотрим колебания осциллятора, на который помимо квазе-упругих сил действует сила трения. Будем считать, что эта сила трения пропорциональна скорости колебания матерьяльной точки.

F= Fупр+Fтр ; Fупр = -kx ; Fтр = -b * dx/dt ; m * d2 x / dt (ст.2)= -b*dx/dt – kx

Уравнение, описывающее затухающие колебания:

(d2 x / dt (ст2)) + b/m * dx/dt + kx / m = 0 ; Введем обозначения:

w 0 (ст.2) = k/m ; b/m = 2БЕТА ; БЕТА = b/2m; b – коэффициент сопротивления ; (d2 x / dt (ст.2)) + 2БЕТА*dx/dt + w 0 (ст.2) x = 0 ;

БЕТА – коэффициент затухания.

Общее решение этого уравнения будем искать в виде X = A e (ст.ЛЯМДА t).

Подставим это решение в дифференциальное уравнение затухающих колебаний: dx/dt = A ЛЯМДА e (ст. ЛЯМДА t) ; d2 x / dt (ст.2) = A ЛЯМДА (ст.2) e (ст. ЛЯМДА t); A ЛЯМДА (ст.2) e (ст. ЛЯМДА t) + 2bA ЛЯМДА e (ст.ЛЯМДА t) + w 0 (ст.2) A e (ст.ЛЯМДА t) ; Сокращаем:

ЛЯМДА (ст.2) +2БЕТА d + w 0 (ст.2) = 0 – характеристическое уравнение.

Решая его, получаем: X = - БЕТА + - (корень БЕТА (ст.2) – w 0 (ст.2)) =

- БЕТА + - i (корень w 0 (ст.2) – БЕТА (ст.2)) ; Таким образом общее решение исходного дифференциального уравнения можно преобразовать к виду: w = (корень w 0 (ст.2) – БЕТА (ст.2)) ; X (t) = A0 e (ст. – БЕТА t) sin (wt + φ 0) ;

(рисунок – график затухающих колебаний – сжатый синус, все ниже и неже стает по оси OY).

Затухающие колебания не являются периодическими, т.к. максимальное значение колеблющихся величин, достигаемое в некоторый момент времени в последующем никогда не повторяется, поэтому можно говорить об условном периоде затухающих колебаний – T = 2ПИ / w = 2ПИ / (корень w 0 (ст.2) – БЕТА (ст.2)). Если БЕТА >= w 0, то процесс становится апериодическим.

Билет 62.

1. Вынужденные колебания – это колебания, возникающие в колебательной системе под влиянием переменного внешнего воздействия.

Вынужденные колебания осциллятора под действием синусоидальной силы. ; ma = F ; m d2 x / dt (ст.2) = F ; Fупр = - kx ; Fтр = - b dx / dt ; F = F0 sinΩt ; (d2 x / dt (ст.2)) + (2 БЕТА dx / dt) + w 0 (ст.2) = (F0 / m) sinΩt ; Это дифференциальное уравнение описывает вынужденные колебания. В общем случае общее решение этого неоднородного дифференциального уравнения имеет вид: X(t) = X1(t) + X2(t) ; X1(t) является общим решением однородного диф. уравнения, описывающего свободный гармонический затухающий осциллятор. Видно, что после начала действия вынуждающей силы возникает сложный колебательный процесс, состоящий из суммы 2х колебаний – затухающего колебания X1(t) с частотой wt и незатухающего колебания с частотой Ωt. X1(t) за достаточно небольшой промежуток времени затухает и остается только одно колебание с частотой вынужденной силы Ω0. Это время, в течении которого X1(t) затухает, называется временем установки вынужденных колебаний. Чем больше добротность осциллятора, тем больше время установления ТАУ~10 Q/w0 (это время, в течении которого амплитуда затухающего колебания уменьшится в 100 раз).

В общем случае установившееся вынужденное колебание имеет вид:

X = A sin (Ωt + ФИ) ; непосредственно подставляя это выражение в дифференциальное уравнение вынужденного колебания можно получить:

A = F0 / m (корень (w 0 (ст.2) – Ω(ст.2) + ФИ БЕТА (ст.2) Ω (ст.2)) ;

tgФИ = - 2 БЕТА Ω / (w 0 (ст.2) – Ω (ст.2))

1. при Ω=0 ; A = F0 / m w 0 (ст.2) = F0 / k – статическое смещение.

2. при ΩБЕСКОНЕЧНОСТЬ ; A0 ;

Максимум амплитуды вынужденных колебаний достигается при частоте

Ω = (корень w 0 (ст.2) – БЕТА (ст.2)) ;

При частоте w = (корень w 0 (ст.2) – БЕТА (ст.2)) амплитуда достигает максимума: Amax = F0 / 2 m БЕТА Ω

Явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты вынужденной силы с соответственной частотой колебаний системы называется резонансом. Амплитуда колебаний при резонансе зависит от затухания, чем оно больше, тем меньше амплитуда. При нулевом затуханиии амплитуда колебаний при резонансе достигает бесконечно большой величины.