
Приклад 4.8.
4.2. Дія стаціонарного випадкового процесу на лдс
У попередньому підрозділі ми розглянули стохастичний аналіз в рамках кореляційної теорії дії на ЛДС дискретного випадкового процесу без будь-яких обмежень на його ймовірнісні характеристики. Тепер розглянемо дію на ЛДС випадкового процесу, який задовольняє умовам стаціонарності (див. п. 2.4). Оскільки ми розглядаємо стохастичний аналіз в рамках кореляційної теорії, то обмежимось стаціонарністю у широкому розумінні.
Отже
нехай на нестаціонарну ЛДС з імпульсною
характеристикою
![]() діє стаціонарний у широкому розумінні
дискретний випадковий процес
(див. рис. 4.1). На виході маємо відгук
Потрібно знайти його математичне
сподівання
діє стаціонарний у широкому розумінні
дискретний випадковий процес
(див. рис. 4.1). На виході маємо відгук
Потрібно знайти його математичне
сподівання
![]() ,
дисперсію
,
дисперсію
![]() та
кореляційну функцію
та
кореляційну функцію
![]() .
.
Математичне
сподівання. Для
знаходження математичного сподівання
скористаємось формулою (4.2), в якій
врахуємо те, що для стаціонарного процесу
його математичне сподівання не залежить
від часу, тобто
![]() .
Тоді можемо записати
.
Тоді можемо записати
![]() (4.16)
(4.16)
Отже, як бачимо, математичне сподівання відгуку залежить від часу. Таким чином, якщо на нестаціонарну ЛДС діє стаціонарний процес, то на виході отримуємо відгук у вигляді нестаціонарного процесу.
Далі ми не будемо переписувати співвідношення (4.16) з урахуванням фізичної реалізованості ЛДС та відсутності ненульових відліків вхідного процесу на від’ємній вісі часу. Ці співвідношення читач легко може отримати самостійно на основі формули (4.16), замінивши в останній відповідним чином межі підсумовування, як це було зроблено в п. 4.1.
Приклад
4.9.
На ЛДС з імпульсною характеристикою,
поданою у вигляді табл. 4.1, діє стаціонарний
дискретний випадковий процес
з математичним сподіванням
![]() Знайти математичне сподівання
Знайти математичне сподівання
Таблиця 4.1
-
0
1
2
3
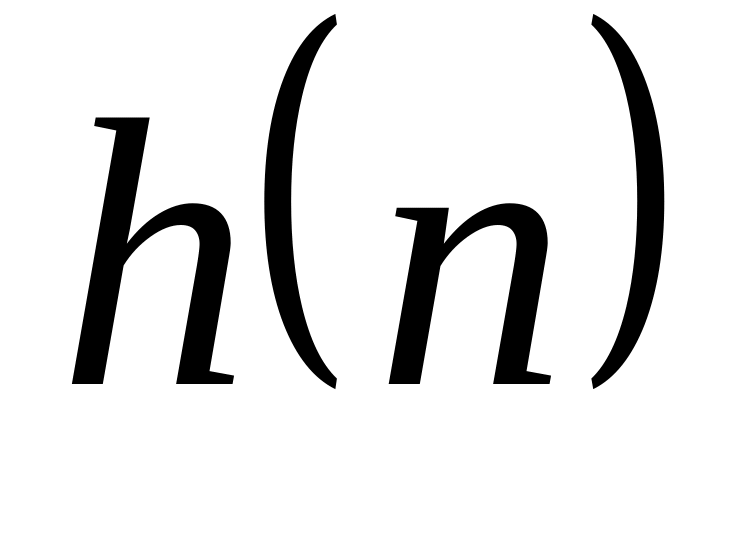
1
0,5
0,25
0,125
процесу на виході ЛДС.
Оскільки імпульсна характеристика є скінченою і залежить лише від поточного часу , то ми маємо справу з нерекурсивною стаціонарною ЛДС. Тому для математичного сподівання процесу на виході системи можемо записати:
![]() ,
,
де нижня
границя підсумовування
![]() у зв’язку з тим, що імпульсна характеристика
має лише 4 ненульових значення, починаючи
з моменту часу
.
Дійсно, при
у зв’язку з тим, що імпульсна характеристика
має лише 4 ненульових значення, починаючи
з моменту часу
.
Дійсно, при
![]() під знаком суми маємо значення імпульсної
характеристики
під знаком суми маємо значення імпульсної
характеристики
![]() .
При
.
При
![]() отримуємо значення імпульсної
характеристики
отримуємо значення імпульсної
характеристики
![]() .
Коли
.
Коли
![]() маємо
маємо
![]() .
Для
маємо
.
Для
маємо
![]() .
Нарешті, якщо
.
Нарешті, якщо
![]() ,
то отримуємо нульове значення імпульсної
характеристики, тобто
,
то отримуємо нульове значення імпульсної
характеристики, тобто
![]() .
Такі ж нульові значення маємо і при
інших значеннях
.
Такі ж нульові значення маємо і при
інших значеннях
![]() .
.
Підставляючи дані із табл. 4.1 в отриману вище формулу, знаходимо
![]() ,
,
Таким чином, математичне сподівання процесу на виході стаціонарної ЛДС, як і на вході, не залежить від часу.
Кореляційна функція відгуку ЛДС при дії стаціонарного процесу. Спершу введемо такі позначення: для центрованого стаціонарного процесу на вході ЛДС
![]()
і для процесу на виході
![]()
Тоді, враховуючи зв’язок між центрованими процесами на вході і виході ЛДС (4.7), кореляційна функція процесу на виході
![]() .
(4.17)
.
(4.17)
Оскільки для стаціонарного процесу кореляційна функція залежить лише від різниці моментів часу (див. п. 2.4), тобто
![]() ,
,
![]()
то (4.17 ) можна записати у такому вигляді
![]()
![]() .
.
Отже якщо на вході нестаціонарної ЛДС діє стаціонарний процес, то на виході маємо нестаціонарний відгук.
1 У тому випадку, коли випадковий сигнал описується ергодичним випадковим процесом, то достатньо мати лише одну реалізацію, але на досить значному часовому інтервалі.
