3.3. Опис лінійних дискретних систем у -області

У попередньому підрозділі ми мали справу з дискретними сигналами як на вході, так і на виході ЛДС, які зображались послідовностями у часовій області. Тому і зв’язок між входом та виходом системи встановлювався на основі її часових характеристик, а саме, імпульсної та перехідної характеристик, а також різницевого рівняння. У останньому випадку система характеризується внутрішніми параметрами – коефіцієнтами рівняння і .

В цьому ж підрозділі будемо розглядати зображення дискретних сигналів ЛДС (і вхідних, і вихідних) на комплексній -площині, тобто будемо мати справу з їх -перетвореннями. Тому і характеристика, яка встановлює зв’язок між -зображенням впливу на ЛДС і -зображенням її реакції буде представляти собою деяку деяку функцію, що залежить від комплексної змінної .

Системна функція. Отже нехай маємо стаціонарну лінійну дискретну систему (див. рис. 3.9) на вході якої діє дискретний сигнал . На виході маємо відгук . Позначимо для цих сигналів їх -перетворення: для вхідного сигналу − і для вихідного − . Відношення -перетворення вихідного сигналу ЛДС до -перетворення вхідного сигналу

(3.47)

називається системною функцією такої системи.

На основі співвідношення (3.47) маємо

, (3.48)

тобто, -перетворення відгуку ЛДС дорівнює добутку -перетворення її вхідного сигналу та системної функції.

Співвідношення (3.48) можна отримати і іншим шляхом. Для цього розглянемо згортку імпульсної характеристики ЛДС з її вхідним сигналом (3.24А). Знайдемо -перетворення лівої і правої частин цього співвідношення. Очевидно, що -перетворення лівої частини співвідношення (3.24А) є зображення на -площині відгуку ЛДС, тобто це . Права частина співвідношення (3.24А) представляє собою згортку імпульсної характеристики системи та вхідного сигналу . Тому на основі властивості 5 -перетворення (див. п. 1.2, формула (1.21)) вона може бути записана у вигляді добутку -зображень імпульсної характеристики та вхідного сигналу . Таким чином, -перетворення лівої і правої частин формули (3.24А) дає співвідношення (3.48), якщо позначити . Із цього можна зробити висновок, що між імпульсною характеристикою ЛДС та її системною функцією існує взаємозв’язок, а саме, системна функція представляє собою -перетворення імпульсної характеристики ЛДС :

. (3.49)

В цій формулі верхня границя підсумовування прямує до нескінченності. В тому ж випадку, коли імпульсна характеристика ЛДС є скінченою, тобто , де , (наприклад, для нерекурсивних систем), в правій частині (3.49) слід покласти всі значення для рівними нулеві.

І навпаки, імпульсна характеристика представляє собою обернене -перетворення системної функції

Приклад 3.9. Маємо лінійну дискретну систему з імпульсною характеристикою , значення якої наведені в табл. 3.4.

Таблиця 3.4

	0	1	2
	2,3	-3.8	1,5

Знайти системну функцію такої ЛДС.

Використовуючи співвідношення (3.49), маємо

.

Отже, на основі отриманих результатів розрахунку цього прикладу можна сказати, що системна функція ЛДС представляє собою поліном змінної : , або, що те ж саме, відношення двох поліномів комплексної змінної : .

Скориставшись різницевим рівнянням для рекурсивної ЛДС (3.29), знайдемо -перетворення його лівої і правої частин. При цьому, згідно з властивостями -перетворення, а саме, адитивності та перетворення зміщеного у часі сигналу (див. п.1.2, властивості 2 і 3 відповідно), маємо

,

або, винісши за знак суми елементи, що не залежать від індексу підсумовування, запишемо:

,

де і − -перетворення вихідного та вхідного сигналів ЛДС відповідно.

Розділивши ліву і праву частини останнього співвідношення на добуток , отримаємо співвідношення

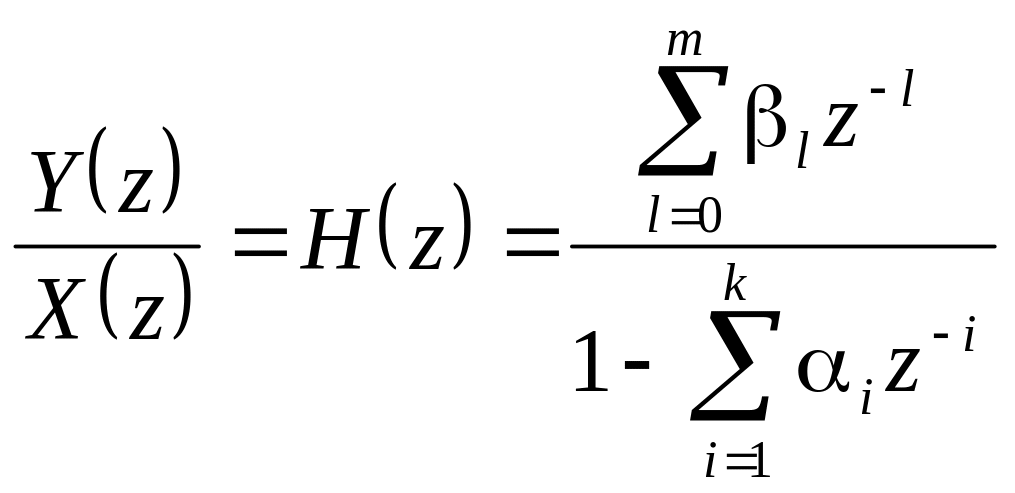, (3.50)

що і зображає собою системну функцію загального виду рекурсивної ЛДС. Якщо помножити чисельник і знаменник правої частини співвідношення (3.50) на , то отримаємо вираз для системної функції відносно комплексної змінної :

. (3.51)

Таким чином системна функція рекурсивної ЛДС представляє собою відношення двох поліномів комплексної змінної .

Знайдемо загальний вигляд системної функції не рекурсивної ЛДС, застосовуючи її різницеве рівняння (3.29А). Для цього, як і у випадку рекурсивної ЛДС, знайдемо спочатку -перетворення лівої і правої частин співвідношення (3.29А). Маємо

.

Розділивши ліву і праву частини останнього співвідношення на -зображення вхідного сигналу , отримаємо системну функцію не рекурсивної ЛДС

, (3.51А)

Яка представляє поліном відносно змінної .

Приклад 3.10. Знайдемо системну функцію рекурсивної ЛДС, розглянутої в прикладі 3.4, скориставшись для цього співвідношенням (3.34), що описує алгоритм роботи такої системи, тобто по суті її різницевим рівнянням, яке зв’язує між собою вхідний і вихідний сигнали системи:

.

Враховуючи властивості -перетворення (адитивність та перетворення зміщеного у часі сигналу, див. п. 1.2), отримаємо -перетворення лівої і правої частин останнього співвідношення. Маємо

,

або

.

Розділивши ліву і праву частину останньої рівності на , отримаємо вираз для системної функції

.

Приклад 3.11. Нерекурсивна ЛДС працює згідно з алгоритмом

. (3.52)

Знайти системну функцію цієї системи.

Знову, як і в попередньому прикладі, застосуємо -перетворення до лівої і правої частин співвідношення (3.52)

.

Розділивши ліву і праву частини останнього співвідношення на -перетворення , отримаємо вираз для системної функції даної системи

.

Порівнюючи результати прикладів 3.10 і 3.11, можна відзначити, що системна функція нерекурсивної ЛДС представляє поліном комплексної змінної , а системна функція рекурсивної ЛДС зображається відношенням двох поліномів комплексної змінної .

Особливі точки (полюси) та нулі системної функції. Системна функція є функція комплексної змінної. Її областю визначення є комплексна площина. Як для аналізу, так і синтезу ЛДС важливим є «поведінка» системної функції на комплексній площині. З цієї точки зору значну інформацію несуть в собі так звані особливі точки (полюси) та нулі системної функції.

Нуль – це значення комплексної змінної , в якому системна функція дорівнює нулеві, тобто

.

Полюс – це значення комплексної змінної , в якому знаменник системної функції дорівнює нулеві, тобто, згідно з формулою (3.51)

.

При цьому , як дробово-раціональна функція комплексної змінної (див. формулу (3.51), у якої знаменник дорівнює нулеві, набуває нескінченного значення, тобто

.

Нулі і полюси зображають на комплексній -площині. При цьому нулі позначають кружечком , а полюси - зірочкою . Сукупність нулів і полюсів системної функції утворюють карту її особливих точок та нулів (див. рис. 3.19).

Значення полюсів і нулів (координати на комплексній площині) знаходять на основі аналітичного виразу для системної функції . При цьому аналітичний вираз записується у вигляді дрібно-раціональної функції, тобто у вигляді відношення двох поліномів відносно комплексної змінної (див. формулу (3.51)). Таке представлення системної функції узгоджується з загальним видом структурної схеми ЛДС (див. рис. 3.13). Зокрема, зауважимо, що чисельник системної функції є -зображення оператора , що відповідає перетворенню (обробці) вхідного сигналу ЛДС, тобто це є зображення на комплексній -площині прямого перетворення згідно з формулою (3.30).

Знаменник системної функції (див. формулу (3.51)) (для рекурсивної системи) – це -зображення оператора , що відповідає перетворенню (обробці) вихідного сигналу ЛДС, тобто це є зображення на комплексній -площині зворотного перетворення згідно з формулою (3.31).

Для фізичної реалізованості ЛДС на їх імпульсні характеристики накладаються певні обмеження (див. п 3.2), що обумовлені принципом причинності. Відповідно до цього принципу накладаються певні обмеження і на системну функцію для фізично існуючих систем. Так, щоб ЛДС була фізично реалізованою, необхідно щоб її системна функція, представлена у вигляді дробово-раціональної функції (3.51), мала степінь полінома чисельника не більшим, ніж степінь полінома знаменника [9], тобто .

З урахуванням цього обмеження можливі два різновиди системних функцій:

1. Степені поліномів чисельника і знаменника системної функції співпадають, тобто згідно з формулою (3.51) і системна функція

. (3.53)

2. Степінь полінома чисельника менше степені полінома знаменника системної функції, тобто .

В першому випадку для знаходження значень полюсі і нулів слід скористатись співвідношенням (3.51) для системної функції, що представляє собою відношення двох поліномів відносно змінної однакового порядку. Значення нулів є розв’язки (корені) рівняння, яке отримуємо, прирівнявши нулеві чисельник системної функції (3.53), тобто

. (3.54)

Розв’язок рівняння (3.54) складається з коренів, тобто маємо нулів: . Серед цих нулів у загальному випадку можуть бути як комплексні попарно спряжені, так і дійсні. Останні можуть співпадати і тоді ми маємо кратні корені. Якщо, наприклад, співпадає нулів (коренів), то кажуть, що вони є -кратними нулями.

Для знаходження значень полюсів системної функції прирівнюють нулеві знаменник дробово-раціонального виразу (3.53). Отримуємо рівняння

.

Розв’язок цього рівняння і дає значення полюсів системної функції . Серед них, як і для нулів, можуть бути попарно спряжені та кратні.

Приклад 3.12. Рекурсивна ЛДС другого порядку має системну функцію виду:

. (3.55)

Знайти нулі і полюси системної функції.

Перш за все помножимо чисельник і знаменник у правій частині співвідношення (3.55) на множник щоб перейти до представлення системної функції у вигляді відношення двох поліномів відносно змінної з додатними степенями, тобто привести вираз для системної функції до виду (3.51). Тоді

. (3.56)

Прирівняємо нулю чисельник системної функції (3.56) і отримаємо рівняння

.

Розв’язавши отримане рівняння, знайдемо значення двох комплексно-спряжених нулів системної функції

і , (3.57)

де - уявна одиниця.

Прирівняємо тепер нулеві знаменник системної функції (3.56) і отримаємо рівняння

.

Розв’язавши отримане рівняння, знайдемо значення двох полюсів системної функції

і . (3.58)

Полюси (3.58) і нулі (3.57) утворюють карту особливих точок і нулів системної функції, яка описується системною функцією (3.55), яка зображена на рис. 3.19.

Рис. 3.19. Карта нулів і полюсів ЛДС із системною функцією (3.55)

Розглянемо тепер другий випадок обчислення нулів і полюсів ЛДС, коли в зображенні її системної функції (3.50) . Тоді системна функція описується дробово-раціональною функцією виду:

. (3.59)

Знаменник системної функції (3.59) подібний до знаменника системної функції (3.53) і тому у другому випадку знаходження значень полюсів нічим не відрізняється від знаходження значень полюсів у першому випадку.

Для знаходження нулів знову ж, як і в першому випадку прирівняємо нулю чисельник правої частини співвідношення (3.59). Отримаємо рівняння

. (3.60)

Винесемо за дужки в правій частині (3.60) спільний елемент

.

Тепер рівняння (3.60) розпалось на два

і .

Розв’язок першого рівняння дає значення нулів, серед яких можуть бути кратні і комплексно-спряжені. Друге ж рівняння має -кратний корінь , тобто ми маємо -кратний нуль. Останні нулі не є інформативними і при дослідженні ЛДС в -області не враховуються.

Для нерекурсивної ЛДС системна функція представляє собою раціональну функцію – поліном -го порядку відносно змінної (див. формулу (3.51А)). Перепишемо цю формулу у такому вигляді:

,

або, привівши до спільного знаменника, запишемо

. (3.61)

Прирівнявши чисельник правої частини співвідношення (3.61) нулю, отримаємо рівняння -го порядку

,

розв’язок якого і дасть нулів рекурсивної ЛДС.

Прирівнявши знаменник правої частини (3.61) до нуля, отримаємо рівняння , розв’язок якого дає -кратний полюс , який є малоінформативним і не враховується при аналізі не рекурсивних ЛДС.

Різновиди запису системних функцій. Зазначимо, що у загальному вигляді системна функція представляє собою відношення двох поліномів комплексної змінної (див. формулу (3.51)). Як відомо з курсу алгебри, поліном -ої степені деякої змінної завжди може бути розкладений в добуток лінійних множників , де - -й корінь утвореного на основі цього полінома рівняння -го порядку. Звідси чисельник і знаменник системної функції (3.51), як многочлени комплексної змінної степені і відповідно (вважаємо, що ), з використанням значень нулів і полюсів можуть бути записані в такому вигляді:

і

.

Тоді системна функція

. (3.62)

Якщо розділити чисельник і знаменник (3.62) на , то остаточно отримаємо представлення системної функції у вигляді відношення добутків найпростіших лінійних множників

. (3.63)

Якщо степені поліномів чисельника і знаменника системної функції співпадають ( ), то представлення (3.63) набуде такого вигляду:

. (3.64)

Приклад 3.13. Системну функцію (3.55) ЛДС, що наведена в прикладі 3.12, записати у вигляді відношення добутків лінійних множників.

У прикладі 3.12 були знайдені значення полюсів (3.58) і нулів (3.57) системної функції (3.55). Оскільки степені чисельника і знаменника системної функції (3.55) співпадають, а саме , а , то системну функцію можна записати, згідно з (3.64), у такому вигляді:

. (3.65)

У справедливості цього розкладення системної функції (3.55) на множники можна упевнитись безпосередньо, перемноживши співмножники, що може виконати читач самостійно.

Системну функцію (3.51) також можна представити у вигляді відношення добутку множників другого порядку з дійсними коефіцієнтами, якщо в представленні (3.63) попарно перемножити співмножники, що відповідають комплексно-спряженим нулям (у чисельникові) і полюсам (у знаменникові).

Розглянемо, для прикладу, на основі представлення (3.63) дві пари таких співмножників. Нехай перша пара відповідає комплексно-спряженим нулям і , де - дійсна частина -го нуля, а - уявна частина -го нуля. Тоді отримаємо такий співмножник другого порядку у чисельникові (3.63)

, (3.66)

де введені позначення і .

Друга пара, згідно зі сказаним вище, представляє собою комплексно-спряжені полюси і , де - дійсна частина -го полюса, а - уявна частина -го полюса. Тоді аналогічно, як і для спряжених нулів, у знаменникові системної функції (3.63) отримуємо співмножник другого порядку

, (3.67)

де введені позначення і .

Будемо вважати, що в формулі (3.63) кількість співмножників у чисельникові і знаменникові парна, тобто числа і є парними і всі нулі, так само як і полюси, є комплексними і попарно спряженими. Тоді таку системну функцію можна записати у вигляді відношення добутків співмножників другого порядку, подібних до (3.66) ,у чисельникові, і (3.67), у знаменникові, тобто

. (3.68)

Якщо в (3.68), окрім вказаних вище припущень, виконується і те, що , то його можна записати у такому вигляді

. (3.68А)

Приклад 3.14. Системну функцію (3.55) ЛДС (див. приклад 3.12) записати у вигляді відношення добутків множників другого порядку.

Перш за все зазначимо, для заданої в прикладі ЛДС її системна функція (3.55) має лише по два комплексно спряжених нулі і полюси, тобто . Якщо це врахувати в співвідношенні (3.68), то, в цьому частинному випадку, ми отримаємо відношення не добутків множників другого порядку а просто відношення двох многочленів другого порядку з дійсними коефіцієнтами.

Це відношення легко отримати, перемноживши окремо чисельник і знаменник добутку дробів у правій частині отриманого у прикладі 3.13 співвідношення (3.65). Маємо

.

Помноживши чисельник у правій частині останнього співвідношення, отримаємо вираз, що співпадає з виразом (3.55). Це пов’язано з тим, що у цьому частинному випадку вихідна системна функція (3.55) сама представляє собою відношення двох поліномів другого порядку відносно комплексної змінної .

Ми розглянули представлення системної функції ЛДС у вигляді відношення добутків лінійних та квадратурних многочленів. По суті розглядалось представлення системної функції у вигляді добутку певних елементарних складових.

Розглянемо тепер представлення системної функції ЛДС у вигляді суми відповідних елементарних складових. Роль елементарних складових будуть відігравати так звані прості дроби відносно комплексної змінної . Таке представлення ґрунтується на відомій з математики теореми [10], що кожний правильний дріб

,

де і - поліноми від змінної , причому степінь полінома чисельника менше степені полінома знаменника , може бути розкладений на суму простих дробів виду:

і . (3.69)

В (3.69) - коефіцієнти розкладення, що визначаються видом полінома , а коефіцієнти - коефіцієнти, які залежать від виду полінома .

Отже, щоб розкласти системну функцію ЛДС на суму простих дробів, потрібно щоб вона представляла собою правильний дріб або дробово-раціональну функцію (3.50), у якої степінь полінома чисельника (відносно змінної ) менше степені полінома знаменника.

Оскільки маємо два різновиди простих дробів (див. формули (3.69)), то можна отримати і два різновиди розкладення системної функції на суму простих дробів.

Перший різновид представляє собою розкладення системної функції ЛДС на суму простих дробів з лінійними знаменниками. Таке представлення системної функції можна реалізувати, використовуючи зображення знаменника останньої у вигляді добутку лінійних множників (див. формулу (3.62))

. (3.70)

Тоді, з урахуванням вказаних вище припущень та розкладення (3.70), системна функція ЛДС може бути представлена таким рядом

, (3.71)

де - коефіцієнти розкладення, які визначаються методом невизначених коефіцієнтів [10]; .

Зауважимо, що зображення системної функції у вигляді (3.71) передбачає, що в розкладенні (3.70) немає кратних полюсів. Якщо ж ця умова не виконується, наприклад, маємо полюс , кратності , то в правій частині (3.70) будемо мати множник , якому в розкладенні (3.71) відповідає група із простих дробів

.

Зрозуміло, що при цьому верхній індекс підсумовування в правій частині (3.71) і добутку в (3.70) буде зменшено на число .

Приклад 3.15. Маємо ЛДС, робота якої описується наступним алгоритмом

. (3.72)

Записати системну функцію такої ЛДС у вигляді суму простих дробів з лінійними знаменниками.

Спочатку знайдемо -перетворення лівої і правої частин співвідношення (3.72)

.

З останнього співвідношення отримаємо системну функцію заданої ЛДС

. (3.73)

Прирівняємо знаменник правої частини співвідношення (3.73) нулеві і отримаємо рівняння відносно змінної :

або

.

Розв’язок цього рівняння дає значення полюсів системної функції (3.73):

і ,

які є комплексно-спряженими.

Застосовуючи далі розкладення системної функції у вигляді суми (3.71), запишемо

. (3.74)

Далі, згідно з методом невизначених коефіцієнтів, зводимо дроби в правій частині співвідношення (3.74) до спільного знаменника і знаходимо їх суму. Маємо

=

. (3.75)

Розглянемо перший і останній дроби співвідношення (3.75). Із рівності дробів випливає рівність їх знаменників і чисельників. Тому, прирівнявши чисельники, маємо

.

Із цієї рівності отримуємо систему рівнянь, прирівнюючи суми її коефіцієнтів у правій і лівій частинах біля змінної з однаковими показниками степені. Для комплексної змінної в степені , тобто для маємо: . Для змінної в нульовій степені, тобто для , маємо . Отже отримали систему із двох рівнянь

Розв’язок цієї системи рівнянь дає такі значення

і .

Остаточно маємо таке представлення системної функції у вигляді суми простих дробів

. (3.76)

Читач може самостійно перевірити, що представлення системної функції (3.76) тотожне початковій системній функції (3.73).

На основі розглянутого прикладу можна зробити висновок, що в представленні системної функції у вигляді (3.71) тип коефіцієнтів розкладення співпадає з типом чисел, що представляють полюси системної функції . Іншими словами, якщо полюс є дійсне число, то і відповідний коефіцієнт розкладення – дійсне число. Якщо маємо комплексно-спряжені полюси, то і коефіцієнти розкладення теж є комплексно-спряжені числа.

Розглянемо тепер зображення системної функції ЛДС у вигляді суми простих дробів зі знаменниками квадратичного типу (прості дроби другого порядку) (див. другу формулу (3.69)). Таке розкладення вимагає таких же обмежень на системну функцію, як і при розкладенні (3.71). Але, окрім цього, потрібно, щоб полюси системної функції були попарно комплексно-спряженими. Тоді кожній парі комплексно-спряжених полюсів буде відповідати поліном другого поряду (див. (3.67)) відносно комплексної змінної і системна функція може бути записана у такому вигляді:

, (3.77)

де - дійсні числові коефіцієнти, що можуть бути визначені методом невизначених коефіцієнтів [10].

Зображення (3.77) може бути отримано також на основі співвідношення (3.71), якщо скласти попарно прості дроби в правій частині останнього, що відповідають комплексно-спряженим полюсам системної функції .

Дійсно, розглянемо два доданки в правій частині (3.71)

і , (3.78)

які відповідають комплексно-спряженим полюсам і , , і знайдемо їх суму. Оскільки для комплексно-спряжених полюсів і коефіцієнти розкладення теж є комплексно-спряженими, то це і відображено для них відповідними позначеннями в формулах (3.78).

Для пари комплексно-спряжених полюсів скористаємось позначеннями, введеними при виведенні формули (3.67). Коефіцієнти розкладення і запишемо в такому вигляді

і ,

де - дійсна частина -го коефіцієнта, а - уявна частина -го коефіцієнта розкладення. Тоді сума дробів (3.78)

, (3.79)

де позначено - коефіцієнт, що дорівнює подвійному значенню дійсної частини коефіцієнта розкладення в (3.71);

- коефіцієнт, що дорівнює подвійній різниці добутку уявних частин коефіцієнта розкладення та полюса і добутку їх дійсних частин; - коефіцієнт, що дорівнює подвійному значенню дійсної частини полюса ; коефіцієнт, що дорівнює квадрату модуля полюса .

Таким чином, використовуючи коментарі до формули (3.79), досить легко можна перейти від зображення системної функції у формі (3.71) до зображення (3.77).

Приклад 3.16. Маємо рекурсивну ЛДС четвертого порядку із системною функцією

. (3.80)

Зобразити системну функцію (3.80) у вигляді суми простих дробів другого порядку.

Прирівняємо нулеві знаменник правої частини співвідношення (3.80)

.

Розв’язавши це рівняння, отримаємо значення полюсів:

;

і

; .

Тоді знаменник, як многочлени четвертого порядку відносно змінної , можна представити у такому вигляді:

. (3.81)

Врахувавши (3.81) в (3.80), можемо записати для системної функції

. (3.82)

Щоб знайти коефіцієнти розкладення , зводимо до спільного знаменника дроби в правій частині співвідношення (3.82) і, зайшовши їх суму, прирівнюємо чисельники дробів у правій і лівій частинах рівності (3.82). Внаслідок цього отримуємо рівняння

.

Далі, прирівнюючи коефіцієнти при однакових степенях змінної , отримуємо систему рівнянь

Розв’язавши цю систему, знаходимо

, , , .

Тепер остаточно можемо записати системну функцію (3.80) у вигляді суми простих дробів другого порядку:

.

Розглянуті вище різновиди зображення системної функції притаманні рекурсивним ЛДС. Для не рекурсивних ЛДС системна функція представляє собою многочлени відносно змінної (3.51А). Тому можливі два різновиди зображення такої системної функції: у вигляді добутку найпростіших лінійних множників або добутку квадратичних співмножників.

Отже, зображення системної функції рекурсивної ДЛС у вигляді добутку найпростіших лінійних множників має такий вигляд:

, (3.83)

де - нулі системної функції.

Якщо порядок ЛДС є парне число, то перемноживши в правій частині співвідношення (3.83) пари з комплексно спряженими нулями, отримаємо зображення системної функції рекурсивної ДЛС у вигляді добутку найпростіших квадратичних множників:

, (3.84)

де і , де, в свою чергу, - дійсна, а - уявна частини -го нуля (див. Формулу (3.66)).

Зауважимо, що коли порядок ЛДС не є парним числом, то представлення (3.84) буде доповнене ще одним, але лінійним, співмножником

,

де - нуль, для якого немає відповідного комплексно-спряженого нуля ( є дійсне число); - парне число, для якого виконується співвідношення .

Приклад 3.17. Маємо нерекурсивну ЛДС четвертого порядку із системною функцією

. (3.85)

Зобразити системну функцію у вигляді добутку простих лінійних множників.

Прирівняємо нулеві праву частину співвідношення (3.85)

.

Розв’язавши це рівняння, отримаємо значення нулів

Тоді, оскільки для даної системної функції , отримаємо, згідно з (3.83), таке зображення

(3.86)

Приклад 3.18. Системну функцію (3.85) нерекурсивної ЛДС, наведену у попередньому прикладі, зобразити у вигляді добутку простих квадратичних множників.

Розглянемо праву частину співвідношення (3.86). Перемноживши співмножники з попарно спряженими нулями, отримаємо шукане зображення:

.

Ланки першого та другого порядків. Знову звернемось до отриманих вище різновидів представлення системних функцій ЛДС. Розглянемо спочатку представлення у вигляді добутку, наприклад, (3.64) і запишемо його так:

, (3.87)

де введено позначення

. (3.88)

Формула (3.88) представляє собою зображення системної функції ЛДС першого порядку. Такі ЛДС першого порядку, коли порядок поліномів чисельника і знаменника співпадають), будемо називати ланками 1-го порядку другого типу, оскільки вони представляють собою деякі «елементарні» ЛДС і на їх основі можна представити системні функції ЛДС більш вищого порядку (див. формулу (3.87)).

Розглянемо тепер представлення системної функції ЛДС у вигляді добутку квадратичних множників (див., наприклад, формулу (3.68А)). Запишемо це зображення так:

, (3.89)

де введено позначення

. (3.90)

Формула (3.90) представляє собою зображення системної функції ЛДС другого порядку. І чисельник і знаменник в (3.90) є поліномами однакового порядку (другого). Такі ЛДС будемо називати ланками 2-го порядку другого типу, і вони також представляють собою деякі «елементарні» ЛДС, на основі яких можна представити системні функції ЛДС більш вищого порядку у вигляді добутку (див. формулу (3.89)).

Розглянемо тепер системну функцію ЛДС у формі (3.71). Таке представлення також можна записати із використанням «елементарних» ЛДС таким чином:

, (3.91)

де позначено

. (3.92)

Це системна функція ЛДС першого порядку, у якої порядок полінома знаменника (маємо поліном першого порядку) більший порядку полінома чисельника (маємо поліном нульового порядку – число). Такі «елементарні» ЛДС будемо називати ланками 1-го порядку першого типу. На основі (3.92) можна представити системні функції ЛДС більш вищого порядку у вигляді суми(див. формулу (3.91)).

Зображення системної функції ЛДС у вигляді суми дробів другого порядку (3.77) дозволяє записати її у вигляді суми «елементарних» ЛДС другого порядку, тобто

, (3.93)

де

.

будемо називати ланками 2-го порядку першого типу, оскільки у них поліном знаменника другого порядку, а порядок полінома чисельника першого порядку, тобто порядок полінома знаменника більше порядку полінома чисельника.

Розглянемо тепер рекурсивну ЛДС, у якої чисельник системної функції представляє собою поліном нульового порядку, а саме

. (3.94)

Така ЛДС носять назву лінійної дискретної системи полюсного вигляду оскільки її системна функція має полюсів, а кратних нулів дорівнюють 0.

Частинним, але важливим, різновидом ЛДС полюсного вигляду є так звані базові ланки 1-го та 2-го порядків. Системна функція базової ланки 1-го порядку має вигляд

. (3.95)

Системна функція базової ланки 2-го порядку має вигляд

. (3.96)

Прирівнявши знаменник правої частини співвідношення (3.95), отримаємо рівняння , розв’язавши яке, знаходимо значення полюса базової ланки 1-го порядку

.

Ця базова ланка має також один нуль .

Аналогічним чином для базової ланки 2-го порядку отримуємо рівняння , розв’язок якого дає значення полюсів

і . (3.97)

Базова ланка 2-го порядку має двократний нуль .

Враховуючи означення системної функції (3.47), для (3.95) можемо записати

, або .

Тоді, використовуючи властивості -перетворення, можемо перейти часову область, тобто отримаємо алгоритм роботи базової ланки 1-го порядку (різницеве рівняння):

. (3.98)

Поклавши в (3.98) , отримаємо імпульсну характеристику базової ланки 1-го порядку:

де

Аналогічним чином, використовуючи співвідношення (3.96), можна записати для базової ланки 2-го порядку

.

Тоді алгоритм роботи базової ланки 2-го порядку (різницеве рівняння) буде мати вигляд:

.

Для знаходження імпульсної характеристики базової ланки 2-го порядку згадаємо, що перша пов’язана з системною функцією -перетворенням (див. Формулу (3.49)). Отже, щоб знайти імпульсну характеристику, потрібно знайти обернене -перетворенням системної функції (3.96). Для цього виконаємо розкладення правої частини співвідношення (3.96) на суму простих дробів, подібно до (3.71),

.

Підставимо в праву частину останнього співвідношення вирази для полюсів (3.97) і отримаємо

.

Застосовуючи метод невизначених коефіцієнтів [10](див. приклад 3.15), знаходимо коефіцієнти розкладення:

і .

Тепер можемо записати (див. підрозділ, присвячений методам знаходження оберненого -перетворення) вираз для імпульсної характеристики базової ланки 2-го порядку:

,

1 Динамічний діапазон – це область , в межах якої змінюються значення сигналів, іншими словами, це допустимий розмах варіації рівня сигналу.

2 Тут розглядається саме простір, а не просто множина сигналів, оскільки між сигналами, математичною моделлю яких є функція часу, існують певні співвідношення, наприклад, відстань між двома сигналами, взаємна енергія, скалярний добуток.

3 Для стійких систем, про що буде мова дещо далі.

4 В формулі (3.24А) верхня границя підсумовування скінчена, але враховуючи загальний випадок, коли і імпульсна характеристика, і сам вхідний сигнал є необмеженими у часі, що є характерним при розгляді стійкості ЛДС, то ми далі використовуємо в якості верхньої границі підсумовування нескінченність.

5 Таке розкладення імпульсної характеристики ЛДС ґрунтується на описові характеристик останньої в -області і його суть буде розкрита в наступному підрозділі 3.3.

68