
Вопросы для самоконтроля
1. От движущейся
моторной лодки по обе стороны от ее
бортов распространяются волны. Какие
это волны: продольные или поперечные?
Как
движется поплавок удочки, когда он
оказывается в зоне, где проходит такая
волна? Пусть частота колебаний поплавка
![]() а длина волны
.
Чему равна скорость волны
а длина волны
.
Чему равна скорость волны
а)
![]() б)
б)
![]() в)
в)
![]() ?
?
Укажите правильное соотношение.
2.
В ситуации, описанной в вопросе 1, пусть
максимальная скорость движения поплавка
равна
![]() а амплитуда волны, которая равна половине
разности уровней гребней и впадин
распространяющей волны , равна
.
Тогда эти величины связаны соотношением
а амплитуда волны, которая равна половине
разности уровней гребней и впадин
распространяющей волны , равна
.
Тогда эти величины связаны соотношением
![]()
а)
![]() б)
б)
![]() в)
в)
![]() .
.
Выберете правильный ответ.
3. Проверить, что
функция
![]() даваемая формулой (2), удовлетворяет
уравнению (5).
даваемая формулой (2), удовлетворяет
уравнению (5).
4. Какова размерность
величин
![]() и
?
и
?
5. Будет ли условие возникновения стоячей волны (12) справедливы для веревки у пастушеского кнута, у которой один конец закреплен, а другой – свободен, или в этом случае условие (12) следует изменить на следующее
![]() где
где
![]() (16)
(16)
6. Как вы думаете, если образуется стоячая звуковая волна в открытом сверху колодце, то какая из формул (12) или (16) будет правильной?
Примеры решения задач
Пример
1. За какое
временя
![]() звуковые колебания пройдут расстояние
между точками 1 и 2, если температура
воздуха между ними меняется линейно от
звуковые колебания пройдут расстояние
между точками 1 и 2, если температура
воздуха между ними меняется линейно от
![]() до
до
![]() Скорость звука в воздухе
Скорость звука в воздухе
![]() где
– постоянная.
где
– постоянная.
Р е ш е н и е. Направим
ось
от точки 1 к точке 2 так, что при
![]()
![]() а при
а при
![]()
![]() Линейную зависимость
Линейную зависимость
![]() можно представить в виде
можно представить в виде
![]()
Интегрируя
соотношение
![]() в пределах от
в пределах от
![]() до
до
![]() ,
получим
,
получим
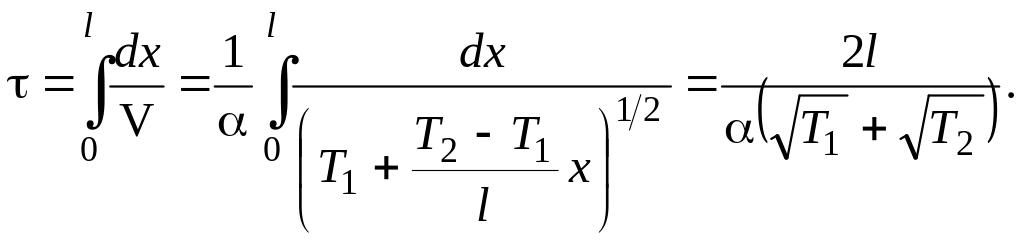
Пример 2. Бегущая
волна имеет вид
![]() где
– в секундах,
–
в метрах. Вычислить частоту
где
– в секундах,
–
в метрах. Вычислить частоту
![]() колебаний, скорость
колебаний, скорость
![]() их распространения и длину волн
.
их распространения и длину волн
.
Р е ш е н и е. Сравнивая заданную в условиях задачи функцию со стандартным выражением (2), имеем
![]()
![]()
![]()
![]()
Тогда
![]() кГц
,
кГц
,
![]() км/с
,
км/с
,
![]() м.
м.
Пример 3. Уравнение плоской звуковой волны имеет вид
![]()
где – в мкм, – в секундах, – в метрах. Найти: а) отношение амплитуды смещения частиц среды к длине волн; б) амплитуду колебаний скорости частиц среды и ее отношение к скорости распространения волн.
Р е ш е н и е. а) по
условию задачи
![]()
![]() Длина волны
Длина волны
![]() м
,
м
,
![]() мкм
. Тогда
мкм
. Тогда
![]()
б) Дифференцируя по времени, получим
![]()
откуда для амплитуды колебаний скорости частиц среды получим
![]() мкм/с
=0,108 м/с.
мкм/с
=0,108 м/с.
Скорость
распространения волны равна
![]() м/с.
Для отношения
м/с.
Для отношения
![]() получим значение
получим значение
![]()
Пример 4. С
какой скоростью распространяется
упругая волна, если в некоторой точке
в один и тот же момент относительная
деформация
![]() и скорость частиц среды
и скорость частиц среды
![]() м/с
?
м/с
?
Р е ш е н и е. Пусть уравнение упругой волны имеет стандартный вид (2). Относительная деформация среды в некоторой точке среды и в некоторый момент времени определяется соотношением
![]()
в то время как скорость частиц среды есть
![]()
Поделив величину
![]() на
на
![]() ,
получим ответ
,
получим ответ
![]() м/с.
м/с.
Пример 5. В
однородной среде распространяется
плоская упругая волна вида
![]() где
где
![]() и
и
![]() – постоянные. Найти разность фаз
колебаний в точках, где амплитуды
смещения частиц среды отличаются друг
от друга на
– постоянные. Найти разность фаз
колебаний в точках, где амплитуды
смещения частиц среды отличаются друг
от друга на
![]() если
если
![]()
![]() и длина волны
и длина волны
![]() см.
см.
Р е ш е н и е. В
некоторый момент времени
разность фаз колебаний в точках
![]() и
и
![]() равна
равна
![]()
Волновое число в
рассматриваемом случае равно
![]() Амплитуды данной затухающей волны в
точках
Амплитуды данной затухающей волны в
точках
![]() и
и
![]() равны
равны
![]() и
и
![]() По условию задачи
По условию задачи
![]()
откуда находим
![]() м.
м.
Окончательно получаем
![]() рад.
рад.
Пример
6. Изотропный
точечный источник, звуковая мощность
которого
![]() Вт,
находится в центре круглого полого
цилиндра радиуса
Вт,
находится в центре круглого полого
цилиндра радиуса
![]() м и высоты
м и высоты
![]() м.
Полагая, что стенки цилиндра полностью
поглощают звук, найти средний поток
энергии, падающий на боковую поверхность
цилиндра. Затухания волн нет.
м.
Полагая, что стенки цилиндра полностью
поглощают звук, найти средний поток
энергии, падающий на боковую поверхность
цилиндра. Затухания волн нет.
Р е ш е н и е. Энергия звуковой волны, испущенная источником, частично падает на боковую поверхность цилиндра, а частично выходит через основания цилиндра. Тогда искомый поток энергии
![]()
г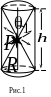 де
де
![]() – телесный угол, вершина которого
находится в месте расположения точечного
источника звука мощностью
– телесный угол, вершина которого
находится в месте расположения точечного
источника звука мощностью
![]() ,
а опирается данный угол на основание
цилиндра. При этом
,
а опирается данный угол на основание
цилиндра. При этом
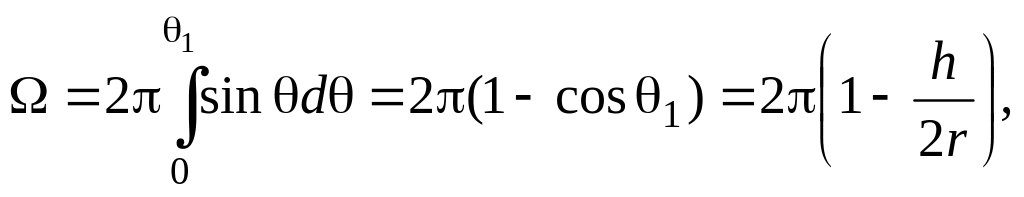
где угол
![]() –
угол полураствора конуса, соответствующему
данному телесному углу (см. рис. 1)
–
угол полураствора конуса, соответствующему
данному телесному углу (см. рис. 1)
В этом выражении
![]() Тогда
Тогда
![]() Вт.
Вт.
Пример 7. Стальная
струна длины
![]() см
и диаметра
см
и диаметра
![]() мм
дает основной тон частоты
мм
дает основной тон частоты
![]() Гц.
Найти силу ее натяжения
Гц.
Найти силу ее натяжения
![]()
Р е ш е н и е. Используем для нахождения величины формулу (13), из которой следует
![]()
где линейная плотность струны равна
![]() где
где
![]() м
,
м
,
а для скорости волн имеем
![]()
Здесь
использовано для основного тона струны
соотношение (12), где
![]() Окончательно
Окончательно
![]() кН.
кН.
