
4. Неинерциальные системы отсчета
Опыт показывает, что причинами ускорения материальной точки могут быть как действие на данную точку каких-то определенных тел, так и свойства системы отсчета, в которой изучается движение точки (действительно, относительно различных систем отсчета ускорение в общем случае будет различным). Если в выбранной системе отсчета причиной ускорения точки является только действие других тел, такая система является инерциальной. Если же причиной ускорения являются не только воздействие других тел, но и свойство самой системы отсчета, то такая система является неинерциальной. Неинерциальные системы отсчета движутся с ускорением относительно инерциальных систем.
Возникает вопрос, а можно ли пользоваться вторым законом Ньютона в неинерциальных системах? Для ответа на этот вопрос рассмотрим два типа неинерциальных систем.
1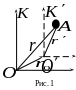 .Пусть
неинерциальная
.Пусть
неинерциальная
![]() -система
движется поступательно по отношению к
инерциальной
-система
движется поступательно по отношению к
инерциальной
![]() -системе
с ускорением
-системе
с ускорением
![]() .
Зададим положение изучаемой материальной
точки
.
Зададим положение изучаемой материальной
точки
![]() (рис.
1) в системах
и
(рис.
1) в системах
и
![]() радиус-векторами
радиус-векторами
![]() и
и
![]() соответственно, а положение начала
отсчета
соответственно, а положение начала
отсчета
![]() системы
относительно начала отсчета
системы
относительно начала отсчета
![]() системы
,
радиус-вектором
системы
,
радиус-вектором
![]() тогда
тогда
![]() .
.
Продифференцировав
это выражение дважды по времени, найдем
связь между ускорениями
![]() и
и
![]() точки
в
системах
и
соответственно
точки
в
системах
и
соответственно
![]()
Умножим обе части
этого уравнения на массу
![]() материальной точки
и перепишем в виде
материальной точки
и перепишем в виде
![]() (1)
(1)
где
![]() – результирующая сила взаимодействия
точки
– результирующая сила взаимодействия
точки
![]() с другими телами. Эта сила не меняется
при переходе от одной системы отсчета
к другой, т.е. она инвариантна
относительно такого перехода.
с другими телами. Эта сила не меняется
при переходе от одной системы отсчета
к другой, т.е. она инвариантна
относительно такого перехода.
Совсем иной характер
имеет составляющая
![]() Эта составляющая возникает не из-за
взаимодействия тел, а из-за ускоренного
движения системы отсчета. Она называется
поступательной
силой инерции.
При переходе к другой ускоренной системе
отсчета меняется и сила инерции. Она не
инвариантна
относительно такого перехода. Кроме
того, сила инерции не подчиняется закону
равенства действия и противодействия.
Если на какое-либо тело действует сила
инерции, то не существует противодействующей
силы, приложенной к другому телу. Таким
образом, второй закон Ньютона (1) для
рассмотренной неинерциальной системы
отсчета запишется в виде
Эта составляющая возникает не из-за
взаимодействия тел, а из-за ускоренного
движения системы отсчета. Она называется
поступательной
силой инерции.
При переходе к другой ускоренной системе
отсчета меняется и сила инерции. Она не
инвариантна
относительно такого перехода. Кроме
того, сила инерции не подчиняется закону
равенства действия и противодействия.
Если на какое-либо тело действует сила
инерции, то не существует противодействующей
силы, приложенной к другому телу. Таким
образом, второй закон Ньютона (1) для
рассмотренной неинерциальной системы
отсчета запишется в виде
![]() (2)
(2)
где
![]() – поступательная сила инерции,
направленная в сторону противоположную
ускорению
– поступательная сила инерции,
направленная в сторону противоположную
ускорению
![]() .
Отсюда следует вывод – при записи
второго закона Ньютона в поступательно
движущейся неинерциальной системе
отсчета кроме сил взаимодействия следует
учитывать поступательную силу инерции.
.
Отсюда следует вывод – при записи
второго закона Ньютона в поступательно
движущейся неинерциальной системе
отсчета кроме сил взаимодействия следует
учитывать поступательную силу инерции.
2. Пусть
неинерциальная
-система
вращается с постоянной угловой скоростью
![]() вокруг оси, неподвижной в инерциальной
-системе.
Возьмем начала отсчета
-
и
-систем
в произвольной точке
на
оси вращения (рис. 2а). Тогда радиус-вектор
точки
в обеих системах отсчета будет один и
тот же:
вокруг оси, неподвижной в инерциальной
-системе.
Возьмем начала отсчета
-
и
-систем
в произвольной точке
на
оси вращения (рис. 2а). Тогда радиус-вектор
точки
в обеих системах отсчета будет один и
тот же:
![]() .
Если точка
неподвижна в
-системе,
то это значит , что ее перемещение
.
Если точка
неподвижна в
-системе,
то это значит , что ее перемещение
![]() в
-системе
за время
в
-системе
за время
![]() обусловлено
только поворотом радиус-вектора
на угол
обусловлено
только поворотом радиус-вектора
на угол![]() (вместе с
-системой)
и равно векторному произведению
(вместе с
-системой)
и равно векторному произведению
![]() (см. раздел “Кинематика твердого тела”).
(см. раздел “Кинематика твердого тела”).
Если же точка
движется относительно
-системы
со скоростью
![]() ,
то за время
она
совершает дополнительное перемещение
,
то за время
она
совершает дополнительное перемещение
![]() (рис.
2а ) и тогда
(рис.
2а ) и тогда
![]() (3)
(3)
Разделив это выражение на , получим следующую формулу преобразования скорости:
![]() ,
(4)
,
(4)
г де
де
![]() и
–
скорости точки
в
-
и
-системах
отсчета соответственно.
и
–
скорости точки
в
-
и
-системах
отсчета соответственно.
Теперь перейдем
к ускорениям. В соответствии с (4)
приращение
![]() вектора
за время
в
-
системе должно складываться из суммы
приращений векторов
вектора
за время
в
-
системе должно складываться из суммы
приращений векторов
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
(5)
.
(5)
Найдем
![]() .
Если точка
движется в
-системе
с
.
Если точка
движется в
-системе
с
![]() ,
то приращение этого вектора в
-системе
обусловлено только его поворотом на
угол
(вместе с
-системой)
и равно, как и в случае с
,
векторному произведению
,
то приращение этого вектора в
-системе
обусловлено только его поворотом на
угол
(вместе с
-системой)
и равно, как и в случае с
,
векторному произведению
![]() .
В этом нетрудно убедиться, совместив
начало вектора
.
В этом нетрудно убедиться, совместив
начало вектора
![]() с
осью вращения (рис. 2б). Если же точка
имеет ускорение
с
осью вращения (рис. 2б). Если же точка
имеет ускорение
![]() в
-системе,
то за время
вектор
получает еще дополнительное приращение
в
-системе,
то за время
вектор
получает еще дополнительное приращение
![]() и тогда
и тогда
![]() .
(6)
.
(6)
Подставим (6) и (3) в равенство (5) и полученное выражение разделим на . В результате найдем следующую формулу преобразования ускорения:
![]() ,
,
где
и
![]() –
ускорения точки
в
-
и
-системах
отсчета. Умножим обе части этого уравнения
на массу
материальной
точки
и перепишем в виде
–
ускорения точки
в
-
и
-системах
отсчета. Умножим обе части этого уравнения
на массу
материальной
точки
и перепишем в виде
![]() (7)
(7)
где – результирующая сила взаимодействия точки с другими телами,
![]() (8)
(8)
– сила Кориолиса,
![]() (9)
(9)
– центробежная
сила (![]() – радиус-вектор, направленный от оси
вращения к точке
).
Сила Кориолиса и центробежная сила –
это силы инерции и обладают теми же
свойствами, что и поступательная сила
инерции. Из формулы (8) следует, что сила
Кориолиса действует только на тела,
которые движутся в неинерциальных
системах отсчета. Центробежная же сила
инерции, как следует из формулы (9),
действует и на покоящиеся и на движущие
тела, и направлена в сторону, противоположную
центростремительному ускорению.
– радиус-вектор, направленный от оси
вращения к точке
).
Сила Кориолиса и центробежная сила –
это силы инерции и обладают теми же
свойствами, что и поступательная сила
инерции. Из формулы (8) следует, что сила
Кориолиса действует только на тела,
которые движутся в неинерциальных
системах отсчета. Центробежная же сила
инерции, как следует из формулы (9),
действует и на покоящиеся и на движущие
тела, и направлена в сторону, противоположную
центростремительному ускорению.
Таким образом, в неинерциальных системах отсчета можно пользоваться вторым законом Ньютона, но необходимо кроме сил взаимодействия учитывать и силы инерции.
