Решение
В
схеме 4 узла. В ветвях 3 и 6 включены
идеальные источники Э.Д.С., эти ветви
соединяются в узле 4. По формуле (4.1)
определяем число уравнений:
.
Действительно,
если за базисный узел принять узел 4 (но
также можно принять узел 1 или 3), то сразу
определяем
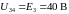и
.
Неизвестным является узловое напряжение
.
Уравнение по методу узловых напряжений имеет вид:
.
где
;
;
;
;
;
.
Определяем
токи
,
,
,
,
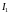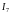по закону Ома:
;
;
;
;
.
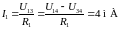Токи
и
определяем по первому закону Кирхгофа:
;
.
Ответ:
,
,
,
,
,
.
Пример 4.4
|
Дано:
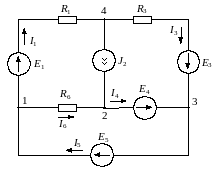
Определить токи в схеме рис. 4.6 методом узловых напряжений.
|
Рис. 4.6 |
;
;
;
;
;
.Решение
За базисный узел в данной схеме можно принимать 1–ый, 2–ой или 3–ий узлы. Рассмотрим решение задачи в случае, если за базисный принят потенциал 3–го узла. Тогда:
.
Поскольку узлы 1 и 2 связаны с 3–им узлом ветвями, содержащими только идеальные источники Э.Д.С. , то:
;
.
Остаётся определить потенциал 4–го относительно 3–го базисного. Составляем одно уравнение:
,
где
–
взаимная
проводимость между 1 и 4 узлами;
– взаимная
проводимость между 2 и 4 узлами;
– собственная
проводимость 4 узла.
Решаем уравнение:
,
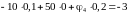откуда:
.
На основании обобщённого закона Ома для участка цепи, определяем токи:
,
откуда
;
;
;
;
.
Токи в четвёртой и пятой ветвях определим по 1–му закону Кирхгофа:
;
.
Ответ:
,
,
,
,
,
.
Пример 4.5
|
Дано:
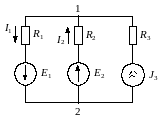
Определить токи в схеме рис. 4.7 методом двух узлов. |
Рис 4.7 |
Решение
За
базисный принимаем второй узел:
Записываем формулу по методу двух узлов:
где
– узловой
ток первого узла;
– собственная
проводимость первого узла.
Тогда
;
.
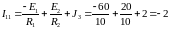Внимание!
В собственной проводимости первого
узла
отсутствует слагаемое
,
так как ветвь, содержащая идеальный
источник тока, имеет бесконечно большое
сопротивление, а значит её проводимость
будет стремиться к нулю.
Определим
напряжение
:
Используя обобщенный закон Ома для участка цепи запишем:
Следовательно, токи в цепи определяются по следующим формулам:
Ответ:
5 Метод эквивалентного генератора
5.1 Основные теоретические положения
Методы решения задач, основанные на теоремах об эквивалентном источнике напряжения и об эквивалентном источнике тока, называются соответственно методом эквивалентного генератора напряжения и методом эквивалентного источника тока.
Эти методы используются в тех случаях, когда по условию задачи требуется определить ток только одной ветви.
Теорема об эквивалентном генераторе напряжения
По
отношению к зажимам произвольно выбранной
ветви оставшаяся активная часть цепи
(активный двухполюсник) может быть
заменена эквивалентным генератором.
Параметры генератора: его Э.Д.С.
равна напряжению на зажимах выделенной
ветви при условии, что эта ветвь
разомкнута, т.е.
;
его внутреннее сопротивление
равно эквивалентному сопротивлению
пассивной электрической цепи со стороны
зажимов выделенной ветви.
|
Рис. 5.1 Иллюстрация к теореме об эквивалентом источнике напряжения |
,
где – эквивалентное сопротивление всей пассивной цепи П.