
- •1.1 Основные теоретические положения. Закон Ома
- •4. Метод узловых напряжений
- •4.1 Основные теоретические положения
- •4.2 Примеры расчета линейных электрических цепей методом узловых напряжений
- •Решение
- •Решение
- •Решение
- •Решение
- •5 Метод эквивалентного генератора
- •5.1 Основные теоретические положения
- •Теорема об эквивалентном генераторе напряжения
- •Теорема об эквивалентном генераторе тока
- •5.2 Примеры расчета линейных электрических цепей методом эквивалентного генератора
- •Решение
- •Решение
1.1 Основные теоретические положения. Закон Ома
Участок ветви, содержащий один или несколько источников энергии, является активным. Рассмотрим участок электрической цепи (рис. 1.1).
|
Рис. 1.1 |
При решении задач по теории электрических цепей выбирают положительное направление тока, которое указывается стрелкой.
Направление тока характеризуется знаком тока. Понятия положительный или отрицательный участок имеют смысл, если сравнивать направление тока в проводнике с некоторым заранее выбранным направлением – так называемым положительным направлением тока.
Запомнить!
Ток в сопротивлении всегда направлен от более высокого потенциала к более низкому, т.е потенциал падает по направлению тока (на рис. 1.1 условно точке «а» присвоим знак «+», а точке «с» – знак «–»).
Э.Д.С., направленная от точки «c» к точке «d», повышает потенциал последней на величину
 (на рис. 1.1 условно зажиму Э.Д.С.,
подключенному к точке «c»,
присвоим знак «–», а зажиму, подключенному
к точке «d»
– знак «+»).
(на рис. 1.1 условно зажиму Э.Д.С.,
подключенному к точке «c»,
присвоим знак «–», а зажиму, подключенному
к точке «d»
– знак «+»).Напряжение
 положительно, когда потенциал точки
«a»
выше, чем потенциал точки «c».
положительно, когда потенциал точки
«a»
выше, чем потенциал точки «c».
При обозначении напряжения (разности потенциалов) на схемах посредством стрелки она направляется от точки высшего потенциала к точке низшего потенциала.
На
рис. 1.1 ток протекает от точки «a»
к точке «c»,
значит, потенциал
 будет меньше
будет меньше
 на величину падения напряжения на
сопротивлении
на величину падения напряжения на
сопротивлении
 ,
которое по закону Ома равно
,
которое по закону Ома равно
 :
:
 .
.
На
участке «c
- d»
Э.Д.С.
 действует в сторону повышения потенциала,
следовательно,
действует в сторону повышения потенциала,
следовательно,
 .
.
Потенциал точки «b» равен:
 .
.
Знак «–» перед Э.Д.С., совпадающей по направлению с током, объясняется следующим образом: напряжение на участке с Э.Д.С. противоположно направлено самой Э.Д.С. и определяемому напряжению.
Напряжение
 найдем как разность потенциалов:
найдем как разность потенциалов:
|
(1.1) |
Ток на участке ab определяют по выражению
|
(1.2) |
Формула (1.2) выражает обобщенный закон Ома, или закон Ома для активного участка цепи.
Из формулы видно, что если ток, напряжение и Э.Д.С. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если Э.Д.С. действует в сторону, противоположную положительному направлению тока, в выражении ставится знак «–».
Закон Ома применяется как для участка ветви, так и для одноконтурной замкнутой схемы.
Пример 1.1
Рис. 1.3 |
Для
схемы рис. 1.3 определим напряжение
Решение Запишем формулу для расчета напряжения между узлом «b» и узлом «a»
Подставим численные значения, получим:
Ответ:
|
Пример 1.2
|
Для
схемы на рис. 1.4 определим напряжения
Решение Используя обобщенный закон Ома для участка цепи, запишем формулы для определения напряжений и : |
Рис. 1.4 |
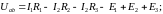
 .
.
Подставим численные значения, получим:
 ;
;
 .
.
Ответ:
 ,
,
 .
.


 .
. .
.
 если
если
 ;
; ;
; ;
; ;
; ;
; .
.
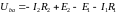 ,
, .
. .
.
 и
и
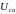 ,
если
,
если
 ;
;
 ;
;
 ;
; ;
;
 ;
;
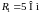 ;
; ;
;
 ;
;
 ;
;
 ;
;
 .
.