Современные проблемы физики / PhysicalReviewpdf / Sidorkin

© ëˉÓÍËÌ Ä.ë., 1999

DOMAIN STRUCTURE AND SWITCHING PROCESSES

IN FERROELECTRICS

A. S. SIDORKIN

The regularities of domain structure formation in ferroelectrics are considered. The questions of domain structure geometry, the equilibrium sizes of domains and the role of kinetic factors in the appearance of metastable domain structures are discussed. The structure and the regularities of the motion of domain walls as intermediate layers between areas with a homogeneous ordered phase are considered.

к‡ТТПУЪ ВМ˚ Б‡НУМУПВ МУТЪЛ ЩУ ПЛ У‚‡- МЛfl ‰УПВММУИ ТЪ ЫНЪЫ-˚ ‚ ТВ„МВЪУ˝ОВНЪ ЛН‡ı. й·ТЫК‰ВМ˚ ‚УФ УТ˚ „ВУПВЪ ЛЛ ‰УПВММУИ ТЪ ЫНЪЫ ˚, ‡‚МУ‚ВТМ˚В‡БПВ ˚ ‰УПВМУ‚ ЛУО¸ НЛМВЪЛ˜ВТНЛı Щ‡Н- ЪУ У‚ ‚ У· ‡БУ‚‡МЛЛ ПВ- Ъ‡ТЪ‡·ЛО¸М˚ı ‰УПВММ˚ı ТЪ ЫНЪЫ , ТЪ УВМЛВ Л Б‡- НУМУПВ МУТЪЛ ‰‚ЛКВМЛfl ФУ Н ЛТЪ‡ООЫ ФВ ВıУ‰- М˚ı ТОУВ‚ ПВК‰Ы У·О‡Т- ЪflПЛ У‰МУ У‰МУ ЫФУ fl- ‰У˜ВММУИ Щ‡Б˚ – ‰УПВМ- М˚ı ТЪВМУН.

СйеЦззАь лнкмднмкА а икйсЦллх иЦкЦдгыуЦзаь З лЦЙзЦнйщгЦднкадАп

Д. л. лаСйкдаз

ЗУ УМВКТНЛИ „УТЫ‰‡ ТЪ‚ВММ˚И ЫМЛ‚В ТЛЪВЪ

ЗЗЦСЦзаЦ

лВ„МВЪУ˝ОВНЪ ЛНЛ – ˝ЪУ ‚В˘ВТЪ‚‡, У·О‡‰‡˛˘ЛВ ‚ УФ В‰ВОВММУП ЪВПФВ ‡ЪЫ МУП ЛМЪВ ‚‡ОВ Т‡ПУ- Ф УЛБ‚УО¸МУИ ЛОЛ ТФУМЪ‡ММУИ, ЪУ ВТЪ¸ ‚УБМЛН‡˛- ˘ВИ ·ВБ ТФВˆЛ‡О¸М˚ı ‚МВ¯МЛı ‚УБ‰ВИТЪ‚ЛИ, ФУОfl-ЛБ‡ˆЛВИ. лФУМЪ‡ММУ ФУОfl ЛБУ‚‡ММУВ ТУТЪУflМЛВВ‡ОЛБЫВЪТfl ‚ ТВ„МВЪУ˝ОВНЪ ЛН‡ı ‚ ‚Л‰В ‰УПВММУИ ТЪ ЫНЪЫ ˚. уЪУ Ъ‡НУВ ‰УПВМ Л ‰УПВММ‡fl ТЪ ЫНЪЫ ‡? СУПВМУП М‡Б˚‚‡ВЪТfl П‡Н УТНУФЛ˜ВТН‡fl У·О‡ТЪ¸ ‚ Н ЛТЪ‡ООВ, ‚ Ф В‰ВО‡ı НУЪУ УИ ‚ТВ ˝ОВПВМЪ‡ М˚В fl˜ВИНЛ ‚ ТВ„МВЪУ˝ОВНЪ ЛНВ ФУОfl ЛБУ‚‡М˚ У‰ЛМ‡НУ- ‚У. з‡Ф ‡‚ОВМЛВ ТФУМЪ‡ММУИ ФУОfl ЛБ‡ˆЛЛ ‚ ТУТВ‰- МЛı ‰УПВМ‡ı ТУТЪ‡‚ОflВЪ УФ В‰ВОВММ˚В Ы„О˚ ‰ Ы„ Т ‰ Ы„УП. йЪ‰ВО¸М˚В ‰УПВМ˚ УЪ‰ВОВМ˚ ‰ Ы„ УЪ ‰ Ы„‡ ‰УПВММ˚ПЛ „ ‡МЛˆ‡ПЛ ЛОЛ ‰УПВММ˚ПЛ ТЪВМН‡ПЛ. лУ‚УНЫФМУТЪ¸ ‰УПВМУ‚ ‡БОЛ˜МУИ У ЛВМЪ‡ˆЛЛ Л М‡Б˚‚‡˛Ъ ‰УПВММУИ ТЪ ЫНЪЫ УИ.

иУ˜ВПЫ П˚ Ы‰ВОflВП Ъ‡НУВ ‚МЛП‡МЛВ, Н‡Б‡ОУТ¸ ·˚, УЪ‰ВО¸МУПЫ Т‚УИТЪ‚Ы П‡ЪВ Л‡ОУ‚? йЪ‚ВЪ Ф УТЪ. ЕУО¸¯ЛМТЪ‚У УЪОЛ˜ЛЪВО¸М˚ı Ф ЛБМ‡НУ‚ ТВ„МВЪУ- ˝ОВНЪ ЛНУ‚ ‚Б‡ЛПУТ‚flБ‡М˚, Л УН‡Б˚‚‡ВЪТfl, ˜ЪУ ‚ ·УО¸¯УИ ТЪВФВМЛ Л МВОЛМВИМ˚В Т‚УИТЪ‚‡, Л ˆВОЛНУП Ф УˆВТТ˚ ФВ ВНО˛˜ВМЛfl ˝ЪЛı П‡ЪВ Л‡ОУ‚, Л ‰ Ы„ЛВ Лı Т‚УИТЪ‚‡ УФ В‰ВОfl˛ЪТfl ‰УПВММУИ ТЪ ЫНЪЫ-УИ. а БМ‡˜ЛЪ, ВТОЛ П˚ ıУЪЛП ФУМflЪ¸ Ф Л У‰Ы ˝ЪЛı fl‚ОВМЛИ Л Ф ЛПВМЛЪ¸ Т‚УИТЪ‚‡ ‰‡ММ˚ı П‡ЪВ Л‡ОУ‚ М‡ Ф ‡НЪЛНВ, П˚ ‰УОКМ˚ ‚˚flТМЛЪ¸ Б‡НУМУПВ МУТЪЛ, НУЪУ ˚В ЫФ ‡‚Оfl˛Ъ Ф УˆВТТ‡ПЛ ‚УБМЛНМУ‚ВМЛfl Л ЛБПВМВМЛВП ‚У ‚ ВПВМЛ ‰УПВММУИ ТЪ ЫНЪЫ ˚.

лаееЦнкавзхв ДлиЦдн ЗйбзадзйЗЦзаь СйеЦззйв лнкмднмкх. ЙЦйеЦнкаь СйеЦзйЗ

З Н ЛТЪ‡ООУЩЛБЛНВ ЛБ‚ВТЪВМ Ъ‡Н М‡Б˚‚‡ВП˚И Ф ЛМˆЛФ д˛ Л, ЫТЪ‡М‡‚ОЛ‚‡˛˘ЛИ Т‚flБ¸ ПВК‰Ы М‡- ˜‡О¸МУИ ТЛППВЪ ЛВИ У·˙ВНЪ‡, ТЛППВЪ ЛВИ ‚УБ‰ВИТЪ- ‚Лfl Л ВБЫО¸ЪЛ Ы˛˘ВИ ТЛППВЪ ЛВИ У·˙ВНЪ‡. лУ„О‡Т- МУ ˝ЪУПЫ Ф ЛМˆЛФЫ, ТЛППВЪ Лfl НУМВ˜МУ„У ТУТЪУflМЛfl‡‚М‡ Ф УЛБ‚В‰ВМЛ˛ ТЛППВЪ ЛЛ ЛТıУ‰МУ„У ТУТЪУflМЛfl М‡ ТЛППВЪ Л˛ ‚УБ‰ВИТЪ‚Лfl. нВ ПЛМ “Ф УЛБ‚В- ‰ВМЛВ” ФУМЛП‡ВЪТfl Б‰ВТ¸ ‚ У·У·˘ВММУП ТП˚ТОВ, ‚ ‰‡ММУП ТОЫ˜‡В ФУ‰ ЫН‡Б‡ММ˚П Ф УЛБ‚В‰ВМЛВП ФУМЛ- П‡ВЪТfl ТУ‚УНЫФМУТЪ¸ ЪВı ˝ОВПВМЪУ‚ ТЛППВЪ ЛЛ ЛТıУ‰МУИ Щ‡Б˚, НУЪУ ˚В ТУı ‡Мfl˛ЪТfl ФУ‰ ‚ОЛflМЛВП ‚МВ¯МВ„У ‚УБ‰ВИТЪ‚Лfl. л ФУПУ˘¸˛ ˝ЪУ„У Ф ЛМˆЛФ‡ ПУКМУ М‡ИЪЛ ТЛППВЪ Л˛ ФУОfl МУИ Щ‡Б˚ М‡ УТМУ‚В БМ‡МЛfl ТЛППВЪ ЛЛ ЛТıУ‰МУИ Щ‡Б˚ Л ТЛППВЪ ЛЛ

Ф‡ ‡ПВЪ ‡ ФУ fl‰Н‡. зУ ˝ЪУ В˘В МВ ‚ТВ. йН‡Б˚‚‡ВЪТfl, ˜ЪУ ЫН‡Б‡ММ˚И Ф ЛМˆЛФ ФУБ‚УОflВЪ М‡ИЪЛ Л „ВУПВЪ-Л˛ ‰УПВММУИ ТЪ ЫНЪЫ ˚, ‚УБМЛН‡˛˘ВИ Ф Л ТУУЪ- ‚ВЪТЪ‚Ы˛˘ВП Щ‡БУ‚УП ФВ ВıУ‰В. щЪУ ‰ВО‡ВЪТfl М‡ УТМУ‚В ТОВ‰Ы˛˘Лı ‡ТТЫК‰ВМЛИ. й·˚˜МУ Щ‡БУ‚˚И ФВ ВıУ‰ ‚ Н ЛТЪ‡ООВ ‚˚Б‚‡М ЛБПВМВМЛВП ЪВПФВ ‡ЪЫ-˚ У· ‡Бˆ‡. зУ ‚В‰¸ ЪВПФВ ‡ЪЫ ‡ – ˝ЪУ ТН‡Оfl МУВ ‚УБ‰ВИТЪ‚ЛВ Л, БМ‡˜ЛЪ, ТУ„О‡ТМУ Ф ЛМˆЛФЫ д˛ Л, ВВ ЛБПВМВМЛВ МВ ‰УОКМУ (ФУ Н ‡ИМВИ ПВ В П‡Н УТНУФЛ˜ВТНЛ) ЛБПВМЛЪ¸ ТЛППВЪ Л˛ У· ‡Бˆ‡. А ВТОЛ ‚ Н‡- НУИ-ОЛ·У В„У ˜‡ТЪЛ (‰УПВМВ) УМ‡ ‚ТВ-Ъ‡НЛ ЛБПВМЛ- О‡Т¸, ˝ЪУ УБМ‡˜‡ВЪ, ˜ЪУ ЫН‡Б‡ММ˚В ‰УПВМ˚ ‰УОКМ˚ Т‰‚УИМЛНУ‚‡Ъ¸Тfl (Т„ ЫФФЛ У‚‡Ъ¸Тfl) Ъ‡НЛП У· ‡БУП, ˜ЪУ·˚ ‚ Т В‰МВП ‰Оfl ˝ЪУИ „ ЫФФ˚ (Ф‡ ˚) ‰УПВМУ‚ ТЛППВЪ Лfl УТЪ‡О‡Т¸ Ъ‡НУИ КВ, Н‡Н Л ‚ ЛТıУ‰МУИ Щ‡- БВ. и Л ˝ЪУП У ЛВМЪ‡ˆЛfl „ ‡МЛˆ ПВК‰Ы ‰УПВМ‡ПЛ,В‡ОЛБЫВП‡fl ‚ Н ЛТЪ‡ООВ ‰‡ММУИ ТЛППВЪ ЛЛ, МВ ПУКВЪ ·˚Ъ¸ Ф УЛБ‚УО¸МУИ. йМ‡ УФ В‰ВОflВЪТfl ЪВПЛ ˝ОВПВМЪ‡ПЛ ТЛППВЪ ЛЛ, НУЪУ ˚В ЛТ˜ВБ‡˛Ъ Ф Л Щ‡- БУ‚УП ФВ ВıУ‰В, ‡ ЛПВММУ ‰УПВМ˚ „ ЫФФЛ Ы˛ЪТfl Ъ‡- НЛП У· ‡БУП, ˜ЪУ·˚ П‡Н УТНУФЛ˜ВТНЛ (ЪУ ВТЪ¸ ‰Оfl „ ЫФФ˚ ‰УПВМУ‚) ‚УТТЪ‡МУ‚ЛЪ¸ ЪВ ˝ОВПВМЪ˚ ТЛППВЪ-ЛЛ, НУЪУ ˚В ЛТ˜ВБОЛ Ф Л Щ‡БУ‚УП ФВ ВıУ‰В ‚ У‰МУ-У‰МЫ˛ ФУОfl МЫ˛ Щ‡БЫ.

щзЦкЙЦнауЦлдаЦ икауазх ЗйбзадзйЗЦзаь СйеЦззйв лнкмднмкх З лЦЙзЦнйщгЦднкадДп

д‡Н П˚ ‚Л‰ВОЛ, ТЛППВЪ ЛИМ˚В Ф Л˜ЛМ˚ У·˙flТМfl˛Ъ ЪУО¸НУ Т‡П Щ‡НЪ ‚УБМЛНМУ‚ВМЛfl ‰УПВМУ‚ Л Лı „ВУПВЪ Л˛, МУ МВ УФ В‰ВОfl˛Ъ ‡БПВ ˚ ‰УПВМУ‚. СВИТЪ‚ЛЪВО¸МУ, Т ЪУ˜НЛ Б ВМЛfl ‚УТТЪ‡МУ‚ОВМЛfl ТЛППВЪ ЛЛ МВУ·ıУ‰ЛПУ ЪУО¸НУ ‡‚ВМТЪ‚У У·˙ВПУ‚ ‰УПВМУ‚ ‡БМУ„У БМ‡Н‡, НУЪУ ˚В Ф Л ˝ЪУП ПУ„ЫЪ ·˚Ъ¸ О˛·˚ПЛ. З ЪУ КВ ‚ ВПfl ‚ ˝НТФВ ЛПВМЪВ ‡БПВ-˚ ‰УПВМУ‚ fl‚Оfl˛ЪТfl ‚ФУОМВ УФ В‰ВОВММ˚ПЛ, Ф Л ˝ЪУП Б‰ВТ¸, Н‡Н Ф ‡‚ЛОУ, М‡·О˛‰‡˛ЪТfl В˘В Л ФВ ЛУ- ‰Л˜ВТНЛВ ТЪ ЫНЪЫ ˚, НУЪУ ˚В МЛН‡Н МВ ТОВ‰Ы˛Ъ ЛБ ТЛППВЪ ЛЛ. иУ˝ЪУПЫ ‚ ‰УФУОМВМЛВ Н ТЛППВЪ ЛИ- М˚П М‡‰У ЛТН‡Ъ¸ В˘В Л ‰ Ы„ЛВ Щ‡НЪУ ˚, УФ В‰ВОfl˛- ˘ЛВ ЫН‡Б‡ММ˚В ı‡ ‡НЪВ ЛТЪЛНЛ ‰УПВМУ‚.

н‡НЛП Щ‡НЪУ УП, У˜В‚Л‰МУ, ‰УОКВМ ·˚Ъ¸ ˝МВ „В- ЪЛ˜ВТНЛИ. щМВ „Лfl КВ, НУЪУ Ы˛ МВУ·ıУ‰ЛПУ ПЛМЛПЛБЛ У‚‡Ъ¸, Ф В‰ТЪ‡‚ОflВЪ ‚ ТОЫ˜‡В ˜ЛТЪ˚ı ТВ„МВЪУ˝- ОВНЪ ЛНУ‚ ТЫППЫ ˝МВ „ЛЛ ‰ВФУОfl ЛБЫ˛˘В„У ФУОfl Т‚flБ‡ММ˚ı Б‡ fl‰У‚ ТФУМЪ‡ММУИ ФУОfl ЛБ‡ˆЛЛ М‡ ФУ- ‚В ıМУТЪЛ ТВ„МВЪУ˝ОВНЪ ЛН‡ Л ˝МВ „ЛЛ ‰УПВММ˚ı „ ‡МЛˆ.

СВИТЪ‚ЛЪВО¸МУ, ‚ ТВ„МВЪУ˝ОВНЪ ЛНВ НУМВ˜М˚ı‡БПВ У‚ ‚ВНЪУ ТФУМЪ‡ММУИ ФУОfl ЛБ‡ˆЛЛ У·flБ‡- ЪВО¸МУ ‚˚ıУ‰ЛЪ М‡ ФУ‚В ıМУТЪ¸ П‡ЪВ Л‡О‡, ‡ ˝ЪУ УБМ‡˜‡ВЪ У· ‡БУ‚‡МЛВ Б‰ВТ¸ Т‚flБ‡ММ˚ı Б‡ fl‰У‚ Л ‚ВБЫО¸Ъ‡ЪВ Ы‚ВОЛ˜ВМЛВ ˝МВ „ЛЛ У· ‡Бˆ‡. З ТВ„МВЪУ- ˝ОВНЪ ЛНВ-ФУОЫФ У‚У‰МЛНВ ЫН‡Б‡ММ˚В Т‚flБ‡ММ˚В Б‡ fl‰˚ ПУ„ЫЪ ·˚Ъ¸ НУПФВМТЛ У‚‡М˚ Б‡ Т˜ВЪ НУМВ˜- МУИ Ф У‚У‰ЛПУТЪЛ П‡ЪВ Л‡О‡. З НО‡ТТЛ˜ВТНЛı ‰Л˝- ОВНЪ ЛН‡ı, Н НУЪУ ˚П УЪМУТЛЪТfl ·УО¸¯ЛМТЪ‚У ТВ„- МВЪУ˝ОВНЪ ЛНУ‚, Ъ‡НУИ ‚УБПУКМУТЪЛ МВЪ. зУ ‚

ФУТОВ‰МЛı ‚ТВ„‰‡ УТЪ‡ВЪТfl ‚УБПУКМУТЪ¸ ЫПВМ¸¯В- МЛfl ˝МВ „ЛЛ ˝ЪУ„У ФУОfl Б‡ Т˜ВЪ ‡Б·ЛВМЛfl Н ЛТЪ‡ОО‡ М‡ ‰УПВМ˚ ( ЛТ. 1). а ˜ВП ПВМ¸¯В УН‡Б˚‚‡ВЪТfl Т В‰- Мflfl ¯Л ЛМ‡ ‰УПВМ‡, ЪВП ПВМ¸¯В ˝МВ „Лfl ‡ТТП‡Ъ-Л‚‡ВПУ„У ‰ВФУОfl ЛБЫ˛˘В„У ФУОfl ( ЛТ. 2, Н Л‚‡fl 1).

д‡Н П˚ ‚Л‰ЛП, Т ЪУ˜НЛ Б ВМЛfl ЪУО¸НУ ‰ВФУОfl Л- БЫ˛˘В„У ФУОfl М‡Л·УОВВ ‚˚„У‰М˚П fl‚ОflВЪТfl ‡Б·ЛВМЛВ М‡ ‚ТВ ·УОВВ Л ·УОВВ ПВОНЛВ ‰УПВМ˚. зУ Ы Ъ‡НУ„У‡Б·ЛВМЛfl ВТЪ¸ Ф УЪЛ‚У·У ТЪ‚Ы˛˘ЛИ Щ‡НЪУ – ˝МВ „Лfl ‰УПВММ˚ı ТЪВМУН. йМЛ Ф В‰ТЪ‡‚Оfl˛Ъ ТУ·УИ ФВ ВıУ‰МУИ ТОУИ ПВК‰Ы ТУТВ‰МЛПЛ ‰УПВМ‡ПЛ, ‚ Ф В- ‰ВО‡ı НУЪУ У„У ‚ВНЪУ ТФУМЪ‡ММУИ ФУОfl ЛБ‡ˆЛЛ ПВМflВЪТfl УЪ В„У БМ‡˜ВМЛfl ‚ У‰МУП ‰УПВМВ ‰У БМ‡˜ВМЛfl ‚ ‰ Ы„УП. З ТВ„МВЪУ˝ОВНЪ ЛН‡ı У· ‡БУ‚‡МЛВ Ъ‡НУ„У ТОУfl Т‚flБ‡МУ Т ‚УБ ‡ТЪ‡МЛВП ˝МВ „ЛЛ ТЛТЪВП˚, ЪУ ВТЪ¸ МВ‚˚„У‰МУ. н‡НЛП У· ‡БУП, ЫПВМ¸¯ВМЛВ Т В‰- МВ„У ‡БПВ ‡ ‰УПВМУ‚ Ф Л‚У‰ЛЪ Н Ы‚ВОЛ˜ВМЛ˛ Лı ˜ЛТО‡ Л, БМ‡˜ЛЪ, Н УТЪЫ ˝МВ „ЛЛ ‰УПВММ˚ı ТЪВМУН. С Ы„ЛПЛ ТОУ‚‡ПЛ, Б‡‚ЛТЛПУТЪ¸ ˝МВ „ЛЛ ‰ВФУОfl Л- БЫ˛˘В„У ФУОfl Л ‰УПВММ˚ı ТЪВМУН УЪ Т В‰МВ„У ‡БПВ-‡ ‰УПВМ‡ d Ф УЪЛ‚УФУОУКМ‡fl ( ЛТ. 2, Н Л‚‡fl 2) Л ‚‡‚МУ‚ВТЛЛ ЫТЪ‡М‡‚ОЛ‚‡ВЪТfl ·‡О‡МТ ПВК‰Ы ЫН‡Б‡М- М˚ПЛ ‚НО‡‰‡ПЛ ‚ ˝МВ „Л˛, УФ В‰ВОfl˛˘ЛИ НУМН ВЪМУВ БМ‡˜ВМЛВ d = d0.

êËÒ. 1. мПВМ¸¯ВМЛВ ˝МВ „ЛЛ ‰ВФУОfl ЛБЫ˛˘В„У ФУОfl ТВ„МВЪУ˝ОВНЪ Л˜ВТНУ„У У· ‡Бˆ‡ НУМВ˜М˚ı‡БПВ У‚ Ф Л ‡Б·ЛВМЛЛ В„У М‡ ‰УПВМ˚. L – ‡Á- ÏÂ Í ËÒڇη ‚‰Óθ ÔÓÎfl ÌÓÈ ÓÒË, d – Ò Â‰Ìflfl ¯Ë Ë̇ ‰ÓÏÂ̇

F

3

1

2

êËÒ. 2. ᇂЛТЛПУТЪ¸ УЪ Т В‰МВИ ¯Л ЛМ˚ ‰УПВМ‡ d ФУ‚В ıМУТЪМУИ ФОУЪМУТЪЛ ˝МВ „ЛЛ ‰ВФУОfl ЛБЫ- ˛˘В„У ФУОfl (1), ФУ‚В ıМУТЪМУИ ФОУЪМУТЪЛ ˝МВ - „ЛЛ ‰УПВММ˚ı ТЪВМУН (2) Ë ÒÛÏÏ˚ ˝ÚËı ˝Ì „ËÈ (3). d0 – ‡‚МУ‚ВТМ‡fl ¯Л ЛМ‡ ‰УПВМ‡, ТУУЪ‚ВЪТЪ‚Ы˛- ˘‡fl ПЛМЛПЫПЫ ЩЫМНˆЛЛ F (Í Ë‚‡fl 3)

äÓ΢ÂÒÚ‚ÂÌÌÛ˛ ÓˆÂÌÍÛ ‚Â΢ËÌ˚ d0 ПУКМУ Т‰ВО‡Ъ¸ ТОВ‰Ы˛˘ЛП Ф УТЪ˚П У· ‡БУП. иУ‚В ıМУТЪ- М‡fl ФОУЪМУТЪ¸ ˝МВ „ЛЛ ‰ВФУОfl ЛБЫ˛˘В„У ФУОfl F1 ФУОЫ˜‡ВЪТfl ФЫЪВП ЫПМУКВМЛfl У·˙ВПМУИ ФОУЪМУТЪЛ ˝МВ „ЛЛ ‰ВФУОfl ЛБЫ˛˘В„У ФУОfl W ̇ ÚÓ΢ËÌÛ ÚÓ„Ó ÒÎÓfl, ‚ Ô Â‰Â·ı ÍÓÚÓ Ó„Ó ˝ÚÓ ÔÓΠÒÛ˘ÂÒÚ‚ÛÂÚ. Ç Ï‡Ú ˇÎÂ, ‡Á·ËÚÓÏ Ì‡ ‰ÓÏÂÌ˚, Í‡Í ‚ˉÌÓ ËÁ ËÒ. 1, ÚÓ΢Ë̇ ˝ÚÓ„Ó ÒÎÓfl ‡‚̇ ‡ÁÏÂ Û ‰ÓÏÂ̇. èÓ˝ÚÓÏÛ F1 = Wd. иУ‚В ıМУТЪМ‡fl ФОУЪМУТЪ¸ ˝МВ „ЛЛ ‰УПВМ- М˚ı ТЪВМУН, Ъ‡НКВ ‡ТТ˜ЛЪ‡ММ‡fl М‡ В‰ЛМЛˆЫ ФУ- ‚В ıМУТЪЛ ТВ„МВЪУ‡НЪЛ‚МУ„У П‡ЪВ Л‡О‡, ФВ ФВМ‰Л- НЫОfl МУИ ФУОfl МУИ УТЛ, ‡‚М‡ ТУУЪ‚ВЪТЪ‚ВММУ F2 = = γL/d, „‰Â γ – ФУ‚В ıМУТЪМ‡fl ФОУЪМУТЪ¸ ˝МВ „ЛЛ ‰УПВММУИ ТЪВМНЛ, L – ЪУО˘ЛМ‡ У· ‡Бˆ‡ ‚ М‡Ф ‡‚ОВМЛЛ ФУОfl МУИ УТЛ. лНО‡‰˚‚‡fl Л ПЛМЛПЛБЛ Ыfl ФУОЫ˜ВММЫ˛ ТЫППЫ ФУ d, ЛПВВП

ФУТНУО¸НЫ γ = Wδ, „‰В δ – ЪУО˘ЛМ‡ ‰УПВММУИ ТЪВМНЛ.

ä‡Í ‚ˉÌÓ ËÁ ÙÓ ÏÛÎ˚ (1), ‡‚ÌÓ‚ÂÒ̇fl ¯Ë Ë̇ ‰ÓÏÂ̇ d0 Ô ÓÔÓ ˆËÓ̇θ̇ L1/2, ЪУ ВТЪ¸ ‰УОКМ‡ ‚УБ-‡ТЪ‡Ъ¸ Т УТЪУП ЪУО˘ЛМ˚ У· ‡Бˆ‡. лУ„О‡ТМУ (1),‡‚МУ‚ВТМ‡fl ¯Л ЛМ‡ ‰УПВМУ‚ Щ‡НЪЛ˜ВТНЛ Ф В‰- ТЪ‡‚ОflВЪ ТУ·УИ Т В‰МВВ „ВУПВЪ Л˜ВТНУВ ПВК‰Ы L Ë δ. èÓ˝ÚÓÏÛ Ò Â‰Ì Á̇˜ÂÌË d0 „У ‡Б‰У ·УО¸¯В ‡БПВ-‡ ˝ОВПВМЪ‡ МУИ fl˜ВИНЛ, ЪУ ВТЪ¸ ‰УПВМ˚ ‰ВИТЪ‚Л- ЪВО¸МУ Ф В‰ТЪ‡‚Оfl˛Ъ ТУ·УИ П‡Н УТНУФЛ˜ВТНЛВ У·-‡БУ‚‡МЛfl. д ЪУПЫ КВ УМУ „У ‡Б‰У ПВМ¸¯В ‡БПВ ‡ Н ЛТЪ‡ОО‡ Л, БМ‡˜ЛЪ, ПУКМУ „У‚У ЛЪ¸ У ‰УПВММУИ ТЪ ЫНЪЫ В УЪ‰ВО¸МУ„У У· ‡Бˆ‡.

СйеЦззДь лнкмднмкД З млгйЗаьп щдкДзакйЗДзаь

лийзнДззйв ийгькабДсаа

З ТВ„МВЪУ˝ОВНЪ ЛН‡ı ‚ УЪОЛ˜ЛВ УЪ ЩВ УП‡„МВЪЛНУ‚ ТЫ˘ВТЪ‚ЫВЪ ЫМЛН‡О¸М˚И Щ‡НЪУ , ФУБ‚УОfl˛- ˘ЛИ ‚ОЛflЪ¸ М‡ Т В‰М˛˛ ¯Л ЛМЫ ‰УПВМУ‚. щЪУЪ Щ‡НЪУ Т‚flБ‡М Т ‚УБПУКМУТЪ¸˛ ˝Н ‡МЛ У‚‡МЛfl ТФУМЪ‡ММУИ ФУОfl ЛБ‡ˆЛЛ МУТЛЪВОflПЛ ˝ОВНЪ Л˜ВТНУ„У Б‡ fl‰‡, М‡Ф ЛПВ , ‚ У·˙ВПВ П‡ЪВ Л‡О‡. щЪУ ФУ‰ ‡БЫПВ‚‡ВЪ М‡ОЛ˜ЛВ Б‡ПВЪМУИ Ф У‚У‰ЛПУТЪЛ ЛОЛ НУМˆВМЪ ‡ˆЛЛ Т‚У·У‰М˚ı МУТЛЪВОВИ, НУЪУ ‡flВ‡ОЛБЫВЪТfl, М‡Ф ЛПВ , ‚ ТВ„МВЪУ˝ОВНЪ ЛН‡ı-ФУОЫ- Ф У‚У‰МЛН‡ı. щН ‡МЛ У‚‡МЛВ ТФУМЪ‡ММУИ ФУОfl Л- Б‡ˆЛЛ Т‚У·У‰М˚ПЛ МУТЛЪВОflПЛ Б‡ fl‰‡ ЫПВМ¸¯‡ВЪ ˝МВ „Л˛ ‰ВФУОfl ЛБЫ˛˘В„У ФУОfl Л ТУУЪ‚ВЪТЪ‚ВММУ Ы‚ВОЛ˜Л‚‡ВЪ d0 ФУ Т ‡‚МВМЛ˛ Т (1). и Л ˝ЪУП, М‡˜Л- М‡fl Т УФ В‰ВОВММУИ НУМˆВМЪ ‡ˆЛЛ МУТЛЪВОВИ n,‡‚ÌÓ‚ÂÒ̇fl ¯Ë Ë̇ d0 ТН‡˜НУП Ы‚ВОЛ˜Л‚‡ВЪТfl ‰У ·ВТНУМВ˜МУТЪЛ, ЪУ ВТЪ¸ Ф УЛТıУ‰ЛЪ ПУМУ‰УПВМЛБ‡- ˆЛfl Н ЛТЪ‡ОО‡. лН‡Б‡ММУВ ıУ У¯У ЛОО˛ТЪ Л ЫВЪТfl Т ФУПУ˘¸˛ ˝МВ „ВЪЛ˜ВТНЛı ‰Л‡„ ‡ПП М‡ ЛТ. 3, Ф В‰ТЪ‡‚Оfl˛˘Лı ФУ‚В ıМУТЪМЫ˛ ФОУЪМУТЪ¸ ТЫП- П‡ МУИ ˝МВ „ЛЛ F3 , ÓÔ Â‰ÂÎfl˛˘ÂÈ ‡‚ÌÓ‚ÂÒÌÛ˛ ¯Ë ËÌÛ ‰ÓÏÂ̇ d0 ‚ Н ЛТЪ‡ОО‡ı Т ‡БОЛ˜МУИ ТЪВФВ- М¸˛ ˝Н ‡МЛ У‚‡МЛfl.

11‡

êËÒ. 3. ᇂЛТЛПУТЪ¸ УЪ Т В‰МВИ ¯Л ЛМ˚ ‰УПВМ‡ ФУ‚В ıМУТЪМУИ ФОУЪМУТЪЛ ˝МВ „ЛЛ ‰ВФУОfl ЛБЫ˛- ˘В„У ФУОfl (1) (1‡ – ·ÂÁ ˝Í ‡ÌË Ó‚‡ÌËfl, 1· – ˝Н ‡- МЛ У‚‡МЛВ ‚ ПУМУ‰УПВММУП Н ЛТЪ‡ООВ), ФУ‚В ı- МУТЪМУИ ФОУЪМУТЪЛ ˝МВ „ЛЛ ‰УПВММ˚ı „ ‡МЛˆ (2) Ë ÒÛÏÏ˚ ˝ÚËı ˝Ì „ËÈ ‰Îfl ÒÎÛ˜‡fl Ò··Ó„Ó (‡) Ë ÒËθ- ÌÓ„Ó (·) ˝Í ‡ÌË Ó‚‡ÌËfl

аБ Т ‡‚МВМЛfl ЛТ. 3 Т ЛТ. 2 ‚Л‰МУ, ˜ЪУ Б‡‚ЛТЛПУТЪ¸ ˝МВ „ЛЛ ‰ВФУОfl ЛБЫ˛˘В„У ФУОfl УЪ d Ф Л М‡- ОЛ˜ЛЛ ˝Н ‡МЛ У‚‡МЛfl ЫКВ МВ УФЛТ˚‚‡ВЪТfl Ф flПУИ ОЛМЛВИ, ‡ Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ ·УОВВ ТОУКМЫ˛ Н Л- ‚Ы˛ 1. Ö ̇˜‡ÎÓ Ô Ë Ï‡Î˚ı d ÒÓ‚Ô‡‰‡ÂÚ Ò ÒÓÓÚ‚ÂÚÒÚ- ‚Û˛˘ÂÈ Ô flÏÓÈ ·ÂÁ ˝Í ‡ÌË Ó‚‡ÌËfl, ‡ Ô Ë ·Óθ¯Ëı d ‚˚ıУ‰ЛЪ М‡ ‡ТЛПФЪУЪЛ˜ВТНУВ БМ‡˜ВМЛВ, УФЛТ˚‚‡- ˛˘ВВ ˝МВ „Л˛ ‰ВФУОfl ЛБЫ˛˘В„У ФУОfl Ф Л М‡ОЛ˜ЛЛ ˝Н ‡МЛ У‚‡МЛfl ‚ ПУМУ‰УПВММУП Н ЛТЪ‡ООВ. лУУЪ- ‚ВЪТЪ‚ВММУ ПВМflВЪТfl Л ТЫПП‡ Н Л‚˚ı 1 Ë 2, ÚÓ ÂÒÚ¸ Í Ë‚‡fl 3, ПЛМЛПЫП НУЪУ УИ ТУУЪ‚ВЪТЪ‚ЫВЪ ‡‚МУ- ‚ВТМУИ ¯Л ЛМВ ‰УПВМ‡ d0 . ìÊ ̇ ËÒ. 3, ‡ ‚ˉÌÓ, ˜ÚÓ ÚӘ͇ Ô ÂÒ˜ÂÌËfl Í Ë‚˚ı 1 Ë 2 Ô Ë Û˜ÂÚ ˝Í ‡- ÌË Ó‚‡ÌËfl Ò‰‚Ë„‡ÂÚÒfl ‚Ô ‡‚Ó ÔÓ Ò ‡‚ÌÂÌ˲ Ò ÚÓ˜- ÍÓÈ Ô ÂÒ˜ÂÌËfl Í Ë‚˚ı 2 Ë 1‡, ЪУ ВТЪ¸ М‡ОЛ˜ЛВ ‰‡- КВ ТО‡·У„У ˝Н ‡МЛ У‚‡МЛfl Ы‚ВОЛ˜Л‚‡ВЪ ФВ ЛУ‰ ‰УПВММУИ ТЪ ЫНЪЫ ˚. ЦТОЛ КВ ˝Н ‡МЛ У‚‡МЛВ ‰У- ТЪ‡ЪУ˜МУ ТЛО¸МУ, ‡ ЛПВММУ М‡˜ЛМ‡fl ТУ ТОЫ˜‡fl, НУ„‰‡ Ф flП‡fl 1· Ô ÓıÓ‰ËÚ ˜Â ÂÁ ÚÓ˜ÍÛ Ô ÂÒ˜ÂÌËfl Ô fl- Ï˚ı 2 Ë 1‡, Í Ë‚‡fl 3 ‚УУ·˘В МВ ЛПВВЪ ПЛМЛПЫП‡ Ф Л НУМВ˜М˚ı БМ‡˜ВМЛflı d. еЛМЛП‡О¸МУВ БМ‡˜ВМЛВ F3 Б‰ВТ¸ В‡ОЛБЫВЪТfl Ф Л d , ˜ЪУ ТУУЪ‚ВЪТЪ‚ЫВЪ ФВ ВıУ‰Ы ‚ ПУМУ‰УПВММУВ ТУТЪУflМЛВ.

СОfl УˆВМНЛ Н ЛЪЛ˜ВТНУИ НУМˆВМЪ ‡ˆЛЛ МУТЛЪВОВИ, Ф Л НУЪУ УИ Ф УЛТıУ‰ЛЪ ПУМУ‰УПВМЛБ‡ˆЛfl, ТУ„О‡ТМУ ЛТ. 3, · МВУ·ıУ‰ЛПУ Ф УТЪУ Ф Л ‡‚МflЪ¸ ‰В·‡В‚ТНЫ˛ ‰ОЛМЫ ˝Н ‡МЛ У‚‡МЛfl, М‡ НУЪУ УИ ТФ‡- ‰‡ВЪ ФУОВ Ф Л М‡ОЛ˜ЛЛ ˝Н ‡МЛ У‚‡МЛfl, ‡‚МУ‚ВТМУИ ¯Л ЛМВ ‰УПВМ‡ d0 , УФ В‰ВОflВПУИ ЩУ ПЫОУИ (1). м˜ЛЪ˚‚‡fl, ˜ЪУ λD = (κT/4πne2)1/2, Ï˚ ÔÓÎÛ˜ËÏ

„‰Â, Í‡Í Ë ‡Ì¸¯Â, d – ЪУО˘ЛМ‡ ‰УПВММУИ ТЪВМНЛ. аБ‚ВТЪМУ, ˜ЪУ Ф Л НУПМ‡ЪМ˚ı ЪВПФВ ‡ЪЫ ‡ı δ

10−7 ТП. ЗПВТЪВ Т У·˚˜МУИ ЪУО˘ЛМУИ У· ‡Бˆ‡ L

0,1 ÒÏ, Òӄ·ÒÌÓ (2), ˝ÚÓ ‰‡ÂÚ n 1014 ÒÏ−3, ЪУ ВТЪ¸ ‚˚ТУНЫ˛, МУ ‚ФУОМВ ‰УФЫТЪЛПЫ˛ НУМˆВМЪ ‡ˆЛ˛ МУТЛЪВОВИ.

зЦкДЗзйЗЦлзхЦ СйеЦззхЦ лнкмднмкх

СУПВММ˚В ТЪ ЫНЪЫ ˚, НУЪУ ˚В П˚ ‡ТТПУЪ ВОЛ ‚˚¯В, fl‚Оfl˛ЪТfl ‡‚МУ‚ВТМ˚ПЛ, ЪУ ВТЪ¸ ТУУЪ‚ВЪТЪ- ‚Ы˛˘ЛПЛ ‡·ТУО˛ЪМУПЫ ПЛМЛПЫПЫ ˝МВ „ЛЛ ТЛТЪВ- П˚. й‰М‡НУ Ъ‡Н‡fl Л‰В‡О¸М‡fl ТЛЪЫ‡ˆЛfl У·˚˜МУ МВ ‰УТЪЛ„‡ВЪТfl. щЪУ Т‚flБ‡МУ Т ·УО¸¯ЛП ‚ ВПВМВП В- О‡НТ‡ˆЛЛ ‰УПВММУИ ТЪ ЫНЪЫ ˚. СУПВММ‡fl ТЪ ЫНЪЫ ‡ ПУКВЪ ЩУ ПЛ У‚‡Ъ¸Тfl ‚ У‰МЛı ЫТОУ‚Лflı, ‡ М‡·О˛- ‰‡Ъ¸Тfl ‚ ‰ Ы„Лı. а ЛБ-Б‡ ·УО¸¯У„У ‚ ВПВМЛ ВВ ВО‡Н- Т‡ˆЛЛ П˚ ·Ы‰ВП М‡·О˛‰‡Ъ¸ МВ ЪЫ ‰УПВММЫ˛ ТЪ ЫНЪЫ-Ы, НУЪУ ‡fl ТУУЪ‚ВЪТЪ‚ЫВЪ ‡‚МУ‚ВТЛ˛ ‚ ЫТОУ‚Лflı М‡·О˛‰ВМЛfl, ‡ ЪЫ, М‡ НУЪУ Ы˛ М‡ОУКЛОЛ УЪФВ˜‡ЪУН Л ЫТОУ‚Лfl ВВ ЩУ ПЛ У‚‡МЛfl, Л Ф УˆВТТ ФВ ВıУ‰‡ Н МУ- ‚УПЫ ТУТЪУflМЛ˛.

дУМН ВЪМ˚ı ТЛЪЫ‡ˆЛИ ПУКВЪ ·˚Ъ¸ ПМУ„У. й˜ВМ¸ ТОУКМУИ fl‚ОflВЪТfl ТЛЪЫ‡ˆЛfl, НУ„‰‡ Н ЛТЪ‡ОО ‡ТЪВЪ Т ‡БЫ ‚ ФУОfl МУИ Щ‡БВ. и Л ˝ЪУП М‡ ‰УПВММЫ˛ ТЪ ЫНЪЫ Ы УН‡Б˚‚‡˛Ъ ‚ОЛflМЛВ ЫКВ ЫТОУ‚Лfl В„У УТ- Ъ‡. З У„ УПМУП ·УО¸¯ЛМТЪ‚В ТОЫ˜‡В‚ ‰УПВММ‡fl ТЪ ЫНЪЫ ‡ ЩУ ПЛ ЫВЪТfl ‚ Ф УˆВТТВ Щ‡БУ‚У„У ФВ В- ıУ‰‡ НУМН ВЪМУ„У У· ‡Бˆ‡ ЛБ Ф‡ ‡˝ОВНЪ Л˜ВТНУ„У, ЪУ ВТЪ¸ МВФУОfl МУ„У, ТУТЪУflМЛfl, ‚ ФУОfl МУВ ТВ„МВЪУ˝ОВНЪ Л˜ВТНУВ. к‡Т˜ВЪ˚ ФУН‡Б˚‚‡˛Ъ, ˜ЪУ ВТОЛ Л‰В‡О¸М˚И (ЪУ ВТЪ¸ ·ВБ‰ВЩВНЪМ˚И) У· ‡БВˆ ·ВТНУМВ˜МУ ПВ‰ОВММУ ФВ В‚У‰ЛЪТfl ˜В ВБ ЪВПФВ ‡ЪЫ Ы Щ‡- БУ‚У„У ФВ ВıУ‰‡ TC Ë ÛÒÎÓ‚Ëfl ˝Í ‡ÌË Ó‚‡ÌËfl ÒÔÓÌ- Ú‡ÌÌÓÈ ÔÓÎfl ËÁ‡ˆËË ‚·ÎËÁË TC Л Ф Л ЪВПФВ ‡ЪЫ В М‡·О˛‰ВМЛfl У‰ЛМ‡НУ‚˚, ЪУ ФВ ЛУ‰ ТЪ ЫНЪЫ ˚, ТЩУ - ПЛ У‚‡ММУИ Ф Л Щ‡БУ‚УП ФВ ВıУ‰В, МВ УЪОЛ˜‡ВЪТfl УЪ ‡‚МУ‚ВТМУ„У. З УТМУ‚В ˝ЪУ„У ОВКЛЪ УЪТЫЪТЪ‚ЛВ ЪВПФВ ‡ЪЫ МУИ Б‡‚ЛТЛПУТЪЛ d0 ‚ (1).

зУ‚‡fl ТЛЪЫ‡ˆЛfl ‚УБМЛН‡ВЪ Ф Л ·˚ТЪ УП УıО‡К‰В- МЛЛ У· ‡Бˆ‡. З ˝ЪУП ТОЫ˜‡В ‚ ‡БОЛ˜М˚ı В„У Ы˜‡ТЪН‡ı МВ ЫТФВ‚‡ВЪ ЫТЪ‡М‡‚ОЛ‚‡Ъ¸Тfl У‰ЛМ‡НУ‚‡fl ЪВПФВ ‡ЪЫ ‡ Л ПУКМУ „У‚У ЛЪ¸ У· УıО‡К‰ВМЛЛ Л ТУУЪ‚ВЪТЪ‚ВММУ ‚УБМЛНМУ‚ВМЛЛ ‰УПВММУИ ТЪ ЫНЪЫ ˚ Ф Л М‡ОЛ˜ЛЛ „ ‡‰ЛВМЪ‡ ЪВПФВ ‡ЪЫ ˚ ‚ П‡ЪВ Л‡ОВ. й·˚˜МУ У· ‡- БВˆ ЛПВВЪ ЩУ ПЫ ЪУМНУИ ФО‡ТЪЛМ˚ Ъ‡НУИ У ЛВМЪ‡- ˆЛЛ, ˜ЪУ М‡Ф ‡‚ОВМЛВ gradT ТУ‚Ф‡‰‡ВЪ Т М‡Ф ‡‚ОВМЛВП ФУОfl МУИ УТЛ. иУТПУЪ ЛП, Н‡НЛВ ˝ЪУ ‚˚БУ‚ВЪ ЛБПВМВМЛfl ‚ ‰УПВММУИ ТЪ ЫНЪЫ В. кВБЫО¸Ъ‡Ъ ОВ„НУ Ф В‰ТН‡Б‡Ъ¸, ВТОЛ ‚˚fl‚ЛЪ¸ ЪВ ЛБПВМВМЛfl, НУЪУ ˚В Ф УЛТıУ‰flЪ Б‰ВТ¸ ‚ Щ‡НЪУ ‡ı, ЩУ ПЛ Ы˛˘Лı ‰У- ПВММЫ˛ ТЪ ЫНЪЫ Ы. е˚ ‚Л‰ВОЛ, ˜ЪУ ˝ЪУ ˝МВ „Лfl ‰В- ФУОfl ЛБЫ˛˘В„У ФУОfl Л ˝МВ „Лfl ‰УПВММ˚ı „ ‡МЛˆ. иВ ‚˚И Щ‡НЪУ ФУ‚В ıМУТЪМ˚И, УМ ЩУ ПЛ ЫВЪТfl Б‡ fl‰‡ПЛ М‡ ФУ‚В ıМУТЪЛ ТВ„МВЪУ˝ОВНЪ ЛН‡, НУЪУ-˚В ‰Оfl ‰‡ММУИ ‚ВОЛ˜ЛМ˚ ФУОfl ЛБ‡ˆЛЛ М‡ ФУ‚В ı- МУТЪЛ Л Ф Л М‡ОЛ˜ЛЛ gradP УТЪ‡˛ЪТfl МВЛБПВММ˚ПЛ. ЗЪУ УИ Щ‡НЪУ У·˙ВПМ˚И. а ‚ МВП Б‰ВТ¸ ВТЪ¸ ·УО¸- ¯ЛВ ЛБПВМВМЛfl. СВИТЪ‚ЛЪВО¸МУ, Ф Л М‡ОЛ˜ЛЛ ‰У- ТЪ‡ЪУ˜МУ„У „ ‡‰ЛВМЪ‡ ЪВПФВ ‡ЪЫ ˚ Щ‡НЪЛ˜ВТНЛ ЪУО¸- НУ ˜‡ТЪ¸ У· ‡Бˆ‡ ФВ ВıУ‰ЛЪ ‚ ФУОfl МУВ ТУТЪУflМЛВ Л, БМ‡˜ЛЪ, ЪУО¸НУ ‚ ˝ЪУИ ˜‡ТЪЛ ВТЪ¸ ‰УПВММ˚В „ ‡МЛˆ˚, ˜ЪУ, ‚ Т‚У˛ У˜В В‰¸, УБМ‡˜‡ВЪ, ˜ЪУ Ф Л ‚˚˜ЛТОВМЛЛ ¯Л ЛМ˚ ‰УПВМ‡ ‚ ЩУ ПЫОЫ (1) МВУ·ıУ‰ЛПУ ФУ‰ТЪ‡‚- ОflЪ¸ МВ ЪУО˘ЛМЫ У· ‡Бˆ‡, ‡ ЪУО˘ЛМЫ ЪУ„У ТОУfl l, ‚ НУЪУ УП Ф УЛТıУ‰ЛЪ Щ‡БУ‚˚И ФВ ВıУ‰. иУТОВ‰М˛˛

Û‰Ó·ÌÓ ‚˚ ‡ÁËÚ¸ ˜Â ÂÁ Á̇˜ÂÌË P0 М‡ ФУ‚В ıМУТЪЛ Л ˜В ВБ „ ‡‰ЛВМЪ ФУОfl ЛБ‡ˆЛЛ: lgradP = P0 , ÓÚÍÛ‰‡ l = P0 /gradP. м˜ВЪ МВУ‰МУ У‰МУТЪЛ ФУОfl ЛБ‡ˆЛЛ ‚‰УО¸ М‡Ф ‡‚ОВМЛfl ФУОfl МУИ УТЛ ‚ПВТЪВ Т Ы˜ВЪУП ЪУ„У, ˜ЪУ Б‡ fl‰˚ ‚ ‰‡ММУП ТОЫ˜‡В ‚УБМЛН‡˛Ъ ЪУО¸НУ М‡ У‰МУИ ФУ‚В ıМУТЪЛ ‚ПВТЪУ ‰‚Ыı, Н‡Н М‡ ЛТ. 1, ‰‡- ВЪ ‰УФУОМЛЪВО¸М˚И НУ˝ЩЩЛˆЛВМЪ 4/5, НУЪУ ˚П, ВТЪВТЪ‚ВММУ, ПУКМУ Ф ВМВ· В˜¸. иУ˝ЪУПЫ, ФУ‰ТЪ‡‚Оflfl ‚˚ ‡КВМЛВ ‰Оfl l ‚ (1), ÔÓÎÛ˜‡ÂÏ

ä‡Í ‚ˉÌÓ ËÁ (3), ̇΢ˠgradT ËÎË gradP Ф Л- ‚У‰ЛЪ Н ЛБПВО¸˜ВМЛ˛ ‰УПВММУИ ТЪ ЫНЪЫ ˚. н‡Н‡fl ТЪ ЫНЪЫ ‡, ‚УБМЛНМЫ‚ Ф Л Щ‡БУ‚УП ФВ ВıУ‰В, ПУКВЪ ‰В К‡Ъ¸Тfl Б‡ЪВП ‰УТЪ‡ЪУ˜МУ ‰УО„У, ıУЪfl Ф Л ‚˚ ‡‚- МЛ‚‡МЛЛ ЪВПФВ ‡ЪЫ ˚ УМ‡ Л ·Ы‰ВЪ МВ ‡‚МУ‚ВТМУИ.

икйЕгЦеД дйщксанаЗзйЙй ийгь

бМ‡˜ЛЪВО¸М˚И Т‡ПУТЪУflЪВО¸М˚И ЛМЪВ ВТ Н ‰У- ПВММ˚П „ ‡МЛˆ‡П У·˙flТМflВЪТfl Лı ˜ ВБ‚˚˜‡ИМУИ ‚‡КМУТЪ¸˛ ‰Оfl В‡ОЛБ‡ˆЛЛ Ф УˆВТТУ‚ ФВ ВНО˛˜В- МЛfl ‚ ПМУ„У‰УПВММ˚ı П‡ЪВ Л‡О‡ı. пУ У¯У ЛБ‚ВТЪМУ, ˜ЪУ Ъ‡НЛВ Ф УˆВТТ˚ ı‡ ‡НЪВ ЛБЫ˛ЪТfl „ЛТЪВ ВБЛТУП, ЪУ ВТЪ¸ МВТУ‚Ф‡‰ВМЛВП ‰Оfl ТВ„МВЪУ˝ОВНЪ ЛНУ‚ Н Л‚˚ı ФУОfl ЛБ‡ˆЛЛ Л ‰ВФУОfl ЛБ‡ˆЛЛ P(E). иУОУ- ‚ЛММУВ ‡ТТЪУflМЛВ ПВК‰Ы ˝ЪЛПЛ Н Л‚˚ПЛ М‡ ФУОВ- ‚УИ УТЛ, ЛБПВ ВММУВ Ф Л БМ‡˜ВМЛЛ P = 0, М‡Б˚‚‡ВЪТfl НУ˝ ˆЛЪЛ‚М˚П ФУОВП Ec . з‡ОЛ˜ЛВ ТФУМЪ‡ММУ ФУОfl ЛБУ‚‡ММУ„У ТУТЪУflМЛfl Ф Уfl‚ОflВЪТfl ‚ ЪУП, ˜ЪУ, ВТОЛ У· ‡ЪЛЪ¸ ‚ МЫО¸ БМ‡˜ВМЛВ ФУОfl ЛБЫ˛˘В„У ФУОfl, П˚ МВ ‰У·¸ВПТfl Ф Л ˝ЪУП У· ‡˘ВМЛfl ‚ МЫО¸ ФУОfl ЛБ‡ˆЛЛ, Н‡Н ‚ У·˚˜М˚ı ОЛМВИМ˚ı ‰Л˝ОВНЪ ЛН‡ı. СОfl ЪУ„У ˜ЪУ·˚ Т‰ВО‡Ъ¸ ˝ЪУ, М‡‰У Ф ЛОУКЛЪ¸ В˘В ФУОВ Т М‡Ф ‡‚ОВМЛВП, Ф УЪЛ‚УФУОУКМ˚П ФУОfl ЛБ‡- ˆЛЛ, Л ТУ БМ‡˜ВМЛВП, Н‡Н ‡Б ‡‚М˚П Ec .

ЗУБМЛНМУ‚ВМЛВ НО˛˜В‚УИ ‰Оfl Ф УˆВТТУ‚ ФВ В- НО˛˜ВМЛfl ı‡ ‡НЪВ ЛТЪЛНЛ – НУ˝ ˆЛЪЛ‚МУ„У ФУОfl ПУКМУ ФУМflЪ¸ ЫКВ ‚ ‡ПН‡ı У‰МУ‰УПВММУ„У Н ЛТ- Ъ‡ОО‡. й‰МУ˜‡ТЪЛ˜М˚В ФУЪВМˆЛ‡О˚, ‚ НУЪУ ˚ı ‰‚Л- КВЪТfl ТВ„МВЪУ‡НЪЛ‚М˚И ЛУМ ‚ ФУОfl МУИ Л МВФУОfl - МУИ Щ‡Б‡ı ( ЛТ. 4), Ф ЛМˆЛФЛ‡О¸МУ УЪОЛ˜‡˛ЪТfl. З МВФУОfl МУИ Щ‡БВ ФУЪВМˆЛ‡О ЛПВВЪ ПЛМЛПЫП Ф Л БМ‡˜ВМЛЛ P = 0, Л ˝ЪУ ТУУЪ‚ВЪТЪ‚ЫВЪ ˝МВ „ВЪЛ˜ВТНУИ ‚˚„У‰МУТЪЛ Б‰ВТ¸ МВФУОfl МУ„У ТУТЪУflМЛfl. З ФУОfl - МУИ Щ‡БВ ФУЪВМˆЛ‡О ТЪ‡МУ‚ЛЪТfl ФУ ПВМ¸¯ВИ ПВ В ‰‚ЫıПЛМЛПЫПМ˚П. й·В Н Л‚˚В М‡ ЛТ. 4 ПУКМУ УФЛТ‡Ъ¸ ФУЪВМˆЛ‡ОУП

„‰В ‚ МВФУОfl МУИ Щ‡БВ А > 0, Ç > 0, ‡ ‚ ÔÓÎfl ÌÓÈ Ù‡Á А < 0, Ç > 0. лУ„О‡ТМУ (4), ‡‚МУ‚ВТМУВ БМ‡˜ВМЛВ ФУ-

Îfl ËÁ‡ˆËË ‚ ÔÓÎfl ÌÓÈ Ù‡Á P = P0 = ± –A ⁄ B.

СОfl ЪУ„У ˜ЪУ·˚ ЫМЛ˜ЪУКЛЪ¸ ТФУМЪ‡ММУ ФУОfl Л- БУ‚‡ММУВ ТУТЪУflМЛВ, МВУ·ıУ‰ЛПУ Ф ЛОУКЛЪ¸ ФУОВ, Ф УЪЛ‚УФУОУКМУВ М‡Ф ‡‚ОВМЛ˛ ФУОfl ЛБ‡ˆЛЛ. щЪУ

12

êËÒ. 4. ‡ – У‰МУ˜‡ТЪЛ˜М˚И ФУЪВМˆЛ‡О, ‚ НУЪУ УП ‰‚ЛКВЪТfl ТВ„МВЪУ‡НЪЛ‚М‡fl ˜‡ТЪЛˆ‡ ‚ МВФУОfl МУИ (1) Ë ÔÓÎfl ÌÓÈ (2) Ù‡Á‡ı; · – ЪУЪ КВ ФУЪВМˆЛ‡О ‚ ФУОfl МУИ Щ‡БВ Ф Л УЪТЫЪТЪ‚ЛЛ (1) Л Ф Л Ф ЛОУКВМЛЛ (2) ˝ÎÂÍÚ Ë˜ÂÒÍÓ„Ó ÔÓÎfl, ‡‚ÌÓ„Ó ÍÓ˝ ˆËÚË‚ÌÓÏÛ

Ф Л‚В‰ВЪ Н ФУ‚˚¯ВМЛ˛ У‰МУ„У ПЛМЛПЫП‡ М‡ ЛТ. 4, ‡

ËН ФУМЛКВМЛ˛ ‰ Ы„У„У. и Л ‰УТЪ‡ЪУ˜МУ ·УО¸¯УП БМ‡˜ВМЛЛ ФУОfl E = Ec ·‡ ¸В ПВК‰Ы ТУТЪУflМЛflПЛ −P0

ËP0 ФУОМУТЪ¸˛ ЫМЛ˜ЪУК‡ВЪТfl ( ЛТ. 4, ·) Л ТВ„МВЪУ‡Н- ЪЛ‚М‡fl ˜‡ТЪЛˆ‡ ПУКВЪ ·ВБ Б‡Ъ Ы‰МВМЛИ ФВ ВıУ‰ЛЪ¸ ‚

ТУТЪУflМЛВ +P0. ÖÒÎË ÓˆÂÌËÚ¸ ÔÓΠEc, НУЪУ УВ Ъ В- ·ЫВЪТfl ‰Оfl ФВ ВФУОfl ЛБ‡ˆЛЛ ‚ У‰МУ˜‡ТЪЛ˜МУИ ПУ‰В- ОЛ, ЪУ УН‡КВЪТfl, ˜ЪУ УМУ МЛН‡Н МВ ТУУЪ‚ВЪТЪ‚ЫВЪ В- ‡О¸МУ М‡·О˛‰‡ВПУПЫ НУ˝ ˆЛЪЛ‚МУПЫ ФУО˛, ‡ М‡ ˆВО˚ı ‰‚‡, ‡ ЪУ Л Ъ Л ФУ fl‰Н‡ ‚ВОЛ˜ЛМ˚ ·УО¸¯В В„У. н‡НУВ ·УО¸¯УВ ‡ТıУК‰ВМЛВ Т ˝НТФВ ЛПВМЪУП Т‚fl- Б‡МУ Т ЪВП, ˜ЪУ В‡О¸М˚И Ф УˆВТТ ФВ ВНО˛˜ВМЛfl УТЫ˘ВТЪ‚ОflВЪТfl МВ Б‡ Т˜ВЪ У‰МУ‚ ВПВММУ„У ФВ ВıУ- ‰‡ ‚ТВı ТВ„МВЪУ‡НЪЛ‚М˚ı ˜‡ТЪЛˆ ‚ Н ЛТЪ‡ООВ ‚ МУ‚УВ ТУТЪУflМЛВ, ‡ Б‡ Т˜ВЪ ОУН‡О¸МУИ ФВ ВФУОfl ЛБ‡ˆЛЛ ‚ У·О‡ТЪЛ ‰‚ЛКЫ˘ВИТfl ‰УПВММУИ „ ‡МЛˆ˚. щЪУ НУООВНЪЛ‚МУВ ‰‚ЛКВМЛВ ˜‡ТЪЛˆ ‚ У·О‡ТЪЛ ФВ ВПВ˘‡˛- ˘ВИТfl „ ‡МЛˆ˚ ЫФ ‡‚ОflВЪТfl ЫКВ ‰ Ы„ЛПЛ (ıУЪfl Л Т‚flБ‡ММ˚ПЛ Т Ф В‰ТЪ‡‚ОВММ˚ПЛ М‡ ЛТ. 4, ·) Б‡НУМУПВ МУТЪflПЛ Л ‰‡ВЪ ЫКВ ЛМУВ ‚˚ ‡КВМЛВ ‰Оfl Ec .

лнкйЦзаЦ СйеЦззхп ЙкДзас З лЦЙзЦнйщгЦднкадДп

СОfl ‚˚flТМВМЛfl ТЪ ЫНЪЫ ˚ ‰УПВММУИ ТЪВМНЛ Н‡Н НУООВНЪЛ‚МУ„У У· ‡БУ‚‡МЛfl ТВ„МВЪУ‡НЪЛ‚М˚ı ˜‡ТЪЛˆ ВТЪВТЪ‚ВММУ У·˙В‰ЛМЛЪ¸ МВТНУО¸НУ (‚ Ф ЛМˆЛФВ ·ВТНУМВ˜МУ ПМУ„У) Л‰ВМЪЛ˜М˚ı У‰МУ˜‡ТЪЛ˜М˚ı ФУЪВМˆЛ‡ОУ‚ Т ‰‚ЫПfl ПЛМЛПЫП‡ПЛ (Ъ‡НЛı, Н‡Н М‡ ЛТ. 4), Т‚flБ‡‚ Лı (‰Оfl Ф УТЪУЪ˚ ЪУО¸НУ ·ОЛК‡И¯Лı ТУТВ- ‰ВИ) УФ В‰ВОВММ˚ПЛ Т‚flБflПЛ – Ф ЫКЛМ‡ПЛ, Н‡Н ФУ- Н‡Б‡МУ М‡ ЛТ. 5. н‡Н‡fl ТıВП‡ ПУ‰ВОЛ ЫВЪ Н ЛТЪ‡ОО Т ‰‚ЫПfl ФУ‰ В¯ВЪН‡ПЛ, „‰В ‡ЪУП˚ У‰МУИ ФУ‰ В¯ВЪНЛ (Ф В‰ФУО‡„‡ВЪТfl, ˜ЪУ УМ‡ КВТЪНУ Б‡ЩЛНТЛ У‚‡М‡) ТУБ‰‡˛Ъ ‰‚Ыı˙flПМ˚И ФУЪВМˆЛ‡О ‰Оfl ФУ‰‚ЛКМ˚ı ‡ЪУПУ‚ ‰ Ы„УИ ФУ‰ В¯ВЪНЛ.

з‡ ˝ЪУИ ПУ‰ВОЛ ıУ У¯У ‚Л‰МУ, Н‡НЛВ Щ‡НЪУ ˚ УФ В‰ВОfl˛Ъ ТЪ ЫНЪЫ Ы ‰УПВММУИ ТЪВМНЛ. л У‰МУИ ТЪУ УМ˚, ˝ЪУ ТЫПП‡ М˚В ˝МВ „ЛЛ Н‡К‰УИ ЛБ ˜‡ТЪЛˆ ‚ Т‚УВП ФУЪВМˆЛ‡ОВ. л ‰ Ы„УИ – ˝МВ „Лfl М‡ЪflМЫЪ˚ı Т‚flБВИ – Ф ЫКЛМУН. йФЪЛП‡О¸МУИ ТЛЪЫ‡ˆЛЛ ТУУЪ- ‚ВЪТЪ‚ЫВЪ ‡‚ВМТЪ‚У ЫН‡Б‡ММ˚ı ‚Л‰У‚ ˝МВ „ЛИ.

a

êËÒ. 5. лЪ УВМЛВ ‰УПВММУИ ТЪВМНЛ ‚ ‡ПН‡ı У‰МУПВ МУИ ПУ‰ВОЛ. ‡ – ‡БПВ ˝ОВПВМЪ‡ МУИ fl˜ВИНЛ

СОfl НУОЛ˜ВТЪ‚ВММУ„У УФЛТ‡МЛfl ТЪ ЫНЪЫ ˚ ‰У- ПВММУИ ТЪВМНЛ, ‚ ЪУП ˜ЛТОВ Л ‰‚ЛКЫ˘ВИТfl, ‡ТТПУЪ-ЛП ТЫПП‡ МЫ˛ ˝МВ „Л˛ ‚ТВı ˜‡ТЪЛˆ, Б‡ФЛТ‡ММЫ˛ ˜В ВБ ФУОfl ЛБ‡ˆЛ˛:

сВМЪ ‡О¸МУВ ТО‡„‡ВПУВ Б‰ВТ¸ ТУУЪ‚ВЪТЪ‚ЫВЪ ТЫПП‡ - МУИ ˝МВ „ЛЛ ˜‡ТЪЛˆ, Ф УМЫПВ У‚‡ММ˚ı МУПВ УП l, ‚ У‰МУ˜‡ТЪЛ˜М˚ı ФУЪВМˆЛ‡О‡ı (4). иУТОВ‰МВВ ı‡ ‡Н- ЪВ ЛБЫВЪ ˝МВ „Л˛ М‡ЪflМЫЪ˚ı Ф ЫКЛМ, ‡ ФВ ‚УВ – НЛМВЪЛ˜ВТНЫ˛ ˝МВ „Л˛ ‰‚ЛКЫ˘ЛıТfl ˜‡ТЪЛˆ. ЦТОЛ ЪУО˘ЛМ‡ ‰УПВММУИ ТЪВМНЛ δ @ ‡, „‰Â ‡ – ‡БПВ ˝ОВПВМЪ‡ МУИ fl˜ВИНЛ, ‚ (5) ‡БЫПМУ ФВ ВИЪЛ Н НУМЪЛМЫ- ‡О¸МУПЫ Ф В‰ВОЫ, „‰В ê(x) – МВФ В ˚‚М‡fl ЩЫМНˆЛfl ‚ М‡Ф ‡‚ОВМЛЛ МУ П‡ОЛ Н „ ‡МЛˆВ. З ˝ЪУП ТОЫ˜‡В

„‰В ФУТЪУflММ‡fl χ ФУОЫ˜ЛО‡ М‡Б‚‡МЛВ НУ ВОflˆЛУММУИ.

м ‡‚МВМЛВ ‰‚ЛКВМЛfl ‰Оfl ФУОfl ЛБ‡ˆЛЛ УФ В‰В- ОflВЪТfl ЛБ ЫТОУ‚Лfl ПЛМЛП‡О¸МУТЪЛ ТЫПП‡ МУИ ˝МВ - „ЛЛ (6) Л ЛПВВЪ ‚Л‰

ЦТОЛ ·˚ ‚ (7) МВ ·˚ОУ ТО‡„‡ВПУ„У, ТУ‰В К‡˘В„У χ (ЪУ ВТЪ¸ П˚ МВ Ы˜ЛЪ˚‚‡ОЛ ·˚ Т‚flБ¸ ПВК‰Ы ˜‡ТЪЛˆ‡ПЛ), Л УЪТЫЪТЪ‚У‚‡О‡ ·˚ МВОЛМВИМУТЪ¸ (B = 0), П˚ ФУОЫ˜Л- ОЛ ·˚ Ы ‡‚МВМЛВ У·˚˜МУ„У УТˆЛООflЪУ ‡. ЦТОЛ А = 0 Ë Ç = 0, ЪУ ВТЪ¸ МВЪ ‚ЪУ УИ ФУ‰ В¯ВЪНЛ, ЩУ ПЛ Ы˛- ˘ВИ ‚ ‰‡ММУП ТОЫ˜‡В ‰‚ЫıПЛМЛПЫПМ˚И ФУЪВМˆЛ‡О, МУ ВТЪ¸ Т‚flБ¸ ПВК‰Ы ТУТВ‰МЛПЛ ˜‡ТЪЛˆ‡ПЛ (χ 0), П˚ ФУОЫ˜‡ВП Ы ‡‚МВМЛВ ·В„Ы˘ВИ ‚УОМ˚, ‡ТФ УТЪ-

‡Ìfl˛˘ÂÈÒfl ÒÓ ÒÍÓ ÓÒÚ¸˛ c0 = χ ⁄ µ. щЪ‡ ‚УОМ‡ УФЛТ˚‚‡ВЪ У·˚˜МУВ ‚УОМУ‚УВ ‚УБПЫ˘ВМЛВ ‚ ТЛТЪВПВ ˜‡ТЪЛˆ (Н ЫКНУ‚ М‡ ЛТ. 5), М‡ıУ‰fl˘ЛıТfl М‡ ‡Т- ТЪУflМЛЛ a ‰ Û„ ÓÚ ‰ Û„‡ Ë Ò‚flÁ‡ÌÌ˚ı Ô ÛÊË̇ÏË.

лЛЪЫ‡ˆЛfl Ф ЛМˆЛФЛ‡О¸МУ ПВМflВЪТfl, НУ„‰‡ П˚ ‰У·‡‚ОflВП ‚ ‚УОМУ‚УВ Ы ‡‚МВМЛВ В˘В Л ТЛО˚, Т‚fl- Б‡ММ˚В Т М‡ОЛ˜ЛВП У‰МУ˜‡ТЪЛ˜МУ„У ФУЪВМˆЛ‡О‡. З

˝ЪУП ТОЫ˜‡В ‰Оfl ТЪ‡ЪЛ˜ВТНУИ ТЛЪЫ‡ˆЛЛ ФУОЫ˜‡ВП‡ТФ В‰ВОВМЛВ ФУОfl ЛБ‡ˆЛЛ ‚ МВФУ‰‚ЛКМУИ ‰УПВММУИ ТЪВМНВ ‚ ‚Л‰В

кВ¯ВМЛВ ‰Оfl ‰‚ЛКЫ˘ВИТfl ТЪВМНЛ ОВ„НУ ПУКВЪ ·˚Ъ¸ ФУОЫ˜ВМУ ЛБ (8), ВТОЛ Ы˜ВТЪ¸, ˜ЪУ P(x, υ) = ê(x − υt), ÚÓ ÂÒÚ¸ Á‡‚ËÒËÚ Ò ‡ÁÛ ÓÚ ÍÓÏ·Ë̇ˆËË ‚Â΢ËÌ x − υt. Ç ˝ÚÓÏ ÒÎÛ˜‡Â Ә‚ˉÌÓ, ˜ÚÓ ∂P/∂t = −υ∂P/∂x, ÓÚÒ˛- ‰‡ ∂2P/δt2 = υ2 ∂2P/∂x2 (υ – ТНУ УТЪ¸ ‰‚ЛКВМЛfl ‰У- ПВММУИ ТЪВМНЛ) Л, БМ‡˜ЛЪ, ‰ЛМ‡ПЛ˜ВТНЫ˛ Б‡‰‡˜Ы ‚

(7) ПУКМУ Т ‡БЫ Т‚ВТЪЛ Н ТЪ‡ЪЛ˜ВТНУИ (‚ ‰‚ЛКЫ˘ВИТfl ‚ПВТЪВ ТУ ТЪВМНУИ ТЛТЪВПВ НУУ ‰ЛМ‡Ъ), ‚‚У‰fl МУ- ‚Ы˛ ФУТЪУflММЫ˛ χ = χ –µυ2 = χ(1 –υ2 ⁄ c20). З В- БЫО¸Ъ‡ЪВ ‡ТФ В‰ВОВМЛВ ФУОfl ЛБ‡ˆЛЛ ‚ ‰‚ЛКЫ˘ВИТfl ТЪВМНВ:

пУ У¯У ‚Л‰МУ, ˜ЪУ ‡ТФ В‰ВОВМЛВ ФУОfl ЛБ‡ˆЛЛ Л ‚ МВФУ‰‚ЛКМУИ Л ‚ ‰‚ЛКЫ˘ВИТfl ТЪВМНВ ОУН‡ОЛБУ‚‡МУ ‚ Ф В‰ВО‡ı ТОУfl Т ЪУО˘ЛМУИ 2δ ‚ ФВ ‚УП Л ТУУЪ‚ВЪ-

ÒÚ‚ÂÌÌÓ 2δ 1 –υ2 ⁄ c20 ‚У ‚ЪУ УП ТОЫ˜‡В. е˚ ‚Л‰ЛП, ˜ЪУ ТЫ˘ВТЪ‚ЫВЪ ОУ ВМˆУ‚ТНУВ ТУН ‡˘ВМЛВ ЪУО˘ЛМ˚ ‰‚ЛКЫ˘ВИТfl ТЪВМНЛ. а ТЫ˘ВТЪ‚ЫВЪ Ф В‰ВО¸М‡fl ТНУ-УТЪ¸ ВВ ‰‚ЛКВМЛfl, ‡‚М‡fl c0 , ÍÓÚÓ ‡fl, Ì‡Ô ËÏ , ‚ ÒÎÛ˜‡Â ˜ËÒÚÓ„Ó Ò„ÌÂÚӽ·ÒÚË͇ ÒÓ‚Ô‡‰‡ÂÚ ÒÓ ÒÍÓ Ó- ÒÚ¸˛ Á‚Û͇.

щзЦкЙаь, щооЦднаЗзДь еДллД а ийСЗаЬзйлнъ СйеЦззйв лнЦзда

ЦТОЛ ФУ‰ТЪ‡‚ЛЪ¸ НУМН ВЪМУВ В¯ВМЛВ (9) ‚ У·- ˘ВВ ‚˚ ‡КВМЛВ (6), ФУТОВ ‚˚˜ЛЪ‡МЛfl ˝МВ „ЛЛ У‰МУ-У‰МУ„У ТУТЪУflМЛfl ФУОЫ˜ЛП ФУ‚В ıМУТЪМЫ˛ ФОУЪМУТЪ¸ ˝МВ „ЛЛ ‰‚ЛКЫ˘ВИТfl ‰УПВММУИ ТЪВМНЛ

á‰ÂÒ¸ γ0 – ˝МВ „Лfl МВФУ‰‚ЛКМУИ ‰УПВММУИ ТЪВМНЛ, ‡

ВТЪ¸ ˝ЩЩВНЪЛ‚М‡fl П‡ТТ‡ ‰‚ЛКЫ˘ВИТfl ‰УПВММУИ ТЪВМНЛ. пУ У¯У ‚Л‰МУ, ˜ЪУ ‚˚ ‡КВМЛfl (10), (11), Н‡Н Л ‚˚ ‡КВМЛВ (9), ЛПВ˛Ъ ВОflЪЛ‚ЛТЪТНЫ˛ ТЪ ЫНЪЫ Ы. А ‰УПВММЫ˛ „ ‡МЛˆЫ, ıУЪfl УМ‡ Л Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ НУООВНЪЛ‚МУВ У· ‡БУ‚‡МЛВ, ПУКМУ Ф В‰ТЪ‡‚ЛЪ¸ ‚ ‚Л- ‰В МВНУИ Н‚‡БЛ˜‡ТЪЛˆ˚ Т ТУ·ТЪ‚ВММ˚ПЛ Ф‡ ‡ПВЪ ‡- ПЛ, Ъ‡НЛПЛ, Н‡Н ТНУ УТЪ¸, ˝МВ „Лfl, П‡ТТ‡ Л ‰ .

м ‡‚МВМЛВ (7) УФЛТ˚‚‡ВЪ ЛБПВМВМЛВ ФУОfl ЛБ‡- ˆЛЛ ‚ Т‚У·У‰МУ ‰‚ЛКЫ˘ВИТfl „ ‡МЛˆВ. и Л ˝ЪУП, Н‡Н Л ‰УОКМУ ·˚Ъ¸, УМУ МВ УФ В‰ВОflВЪ ВВ ТНУ УТЪЛ. З ТУУЪ‚ВЪТЪ‚ЛЛ Т ˝ЪЛП Ы ‡‚МВМЛВП ‰УПВММ‡fl „ ‡МЛˆ‡

ПУКВЪ М‡ıУ‰ЛЪ¸Тfl ‚ О˛·УП ЫТЪУИ˜Л‚УП ТУТЪУflМЛЛ ‰‚ЛКВМЛfl ТУ ТНУ УТЪ¸˛, ЛБПВМfl˛˘ВИТfl УЪ МЫОfl ‰У Ф В‰ВО¸МУ„У БМ‡˜ВМЛfl c0 . л‡ПУ КВ НУМН ВЪМУВ БМ‡- ˜ВМЛВ ТНУ УТЪЛ УФ В‰ВОflВЪТfl Б‰ВТ¸ ЪУО¸НУ М‡˜‡О¸- М˚ПЛ ЫТОУ‚ЛflПЛ ‰‚ЛКВМЛfl. з‡Ф УЪЛ‚, ТНУ УТЪ¸ ‰У- ПВММУИ ТЪВМНЛ ТЪ‡МУ‚ЛЪТfl ‚ФУОМВ УФ В‰ВОВММУИ, ВТОЛ ‚ Ы ‡‚МВМЛВ ‰‚ЛКВМЛfl (7) ‰У·‡‚ЛЪ¸ ‰ЛТТЛФ‡ЪЛ‚- МУВ ТО‡„‡ВПУВ, ‡ Ъ‡НКВ ‚МВ¯МВВ ˝ОВНЪ Л˜ВТНУВ ФУОВ:

З ФВ ‚УП Ф Л·ОЛКВМЛЛ ‡БЫПМУ Ф В‰ФУОУКЛЪ¸, ˜ЪУ ‚ ТО‡·˚ı ФУОflı Ф УЩЛО¸ ЛБПВМВМЛfl ФУОfl ЛБ‡- ˆЛЛ ‚ ‰УПВММУИ ТЪВМНВ, ‰‚ЛКЫ˘ВИТfl ‚У ‚МВ¯МВП ФУОВ, ФУ˜ЪЛ МВ УЪОЛ˜‡ВЪТfl УЪ ТУУЪ‚ВЪТЪ‚Ы˛˘В„У ‡Т- Ф В‰ВОВМЛfl ‰Оfl Т‚У·У‰МУ ‰‚ЛКЫ˘ВИТfl ТЪВМНЛ. м˜Л- Ъ˚‚‡fl КВ, ˜ЪУ Ф УЩЛО¸ Т‚У·У‰МУИ ТЪВМНЛ ЩУ ПЛ Ы- ВЪ ‡‚ВМТЪ‚У ТО‡„‡ВП˚ı ‚ Ы ‡‚МВМЛЛ (7), Л ФУО‡„‡fl, ˜ЪУ ˝ЪУ ‡‚ВМТЪ‚У УТЪ‡ВЪТfl ‚ ТЛОВ Л ‚МЫЪ Л Ы ‡‚МВМЛfl (12), ФУОЫ˜ЛП Ф УТЪУВ ТУУЪМУ¯ВМЛВ

ЗТФУПЛМ‡fl, ˜ЪУ |∂P/∂t| = υ|∂P/∂x|, Л УˆВМЛ‚‡fl ФУТОВ‰М˛˛ Ф УЛБ‚У‰МЫ˛ Н‡Н |∂P/∂x| ≈ P0 /δ, ‰Оfl ТОЫ- ˜‡fl ТО‡·˚ı ФУОВИ ФУОЫ˜ЛП ОЛМВИМЫ˛ Б‡‚ЛТЛПУТЪ¸ ТНУ УТЪЛ ‰УПВММУИ ТЪВМНЛ УЪ ‚МВ¯МВ„У ФУОfl

„‰Â ˜ – ФУ‰‚ЛКМУТЪ¸ ‰УПВММУИ ТЪВМНЛ Л Γ – НУ˝Щ- ЩЛˆЛВМЪ ‚flБНУТЪЛ ‰Оfl ‰‚ЛКВМЛfl ФУОfl ЛБ‡ˆЛЛ. аБ ФУОЫ˜ВММУ„У ТУУЪМУ¯ВМЛfl ‚Л‰МУ, ˜ЪУ ФУ‰‚ЛКМУТЪ¸ ТЪВМНЛ Ф Л Ф У˜Лı ‡‚М˚ı ЫТОУ‚Лflı Ф flПУ Ф УФУ - ˆЛУМ‡О¸М‡ ВВ ¯Л ЛМВ.

и Л‚В‰ВММ˚В ‚˚¯В ‡ТТЫК‰ВМЛfl Л НУМН ВЪМ˚ВВБЫО¸Ъ‡Ъ˚ ıУ У¯У УФЛТ˚‚‡˛Ъ ФУ‚В‰ВМЛВ ЪУО¸НУ ‰УТЪ‡ЪУ˜МУ ¯Л УНЛı ‰УПВММ˚ı ТЪВМУН, НУЪУ ˚В ‚ТВ„‰‡ В‡ОЛБЫ˛ЪТfl ‚ ЩВ УП‡„МВЪЛН‡ı, ‡ ‚ ТОЫ˜‡В ТВ„МВЪУ˝ОВНЪ ЛНУ‚ – ЪУО¸НУ ‚·ОЛБЛ ЪУ˜НЛ д˛ Л TC , „‰В ‚ВОЛ˜ЛМ‡ δ ‚УБ ‡ТЪ‡ВЪ Б‡ Т˜ВЪ ‡БПfl„˜ВМЛfl Н ЛТ- Ъ‡ООЛ˜ВТНУИ В¯ВЪНЛ. и Л ‰УТЪ‡ЪУ˜МУП Ы‰‡ОВМЛЛ УЪ TC ‰УПВММ˚В „ ‡МЛˆ˚ ‚ ТВ„МВЪУ˝ОВНЪ ЛН‡ı ТЪ‡- МУ‚flЪТfl М‡ТЪУО¸НУ ЫБНЛПЛ, ˜ЪУ М‡˜ЛМ‡˛Ъ ˜Ы‚ТЪ‚У- ‚‡Ъ¸ ‰ЛТН ВЪМУТЪ¸ Н ЛТЪ‡ООЛ˜ВТНУИ В¯ВЪНЛ. З ˝ЪУП ТОЫ˜‡В Лı ·УНУ‚УВ ‰‚ЛКВМЛВ Н‡Н ˆВОУ„У fl‚ОflВЪТfl ЪУО¸НУ Н‡КЫ˘ЛПТfl. з‡ Т‡ПУП ‰ВОВ УМУ УТЫ˘В- ТЪ‚ОflВЪТfl Б‰ВТ¸ ФЫЪВП У· ‡БУ‚‡МЛfl Л ФУТОВ‰Ы˛˘В„У‡Б ‡ТЪ‡МЛfl Б‡ У‰˚¯ВИ У· ‡ЪМ˚ı ‰УПВМУ‚ М‡ ‰У- ПВММУИ ТЪВМНВ.

и УˆВТТ У· ‡БУ‚‡МЛfl Б‡ У‰˚¯ВИ М‡ ‰УПВММУИ ТЪВМНВ ВТЪ¸ Ф УˆВТТ ‚В УflЪМУТЪМ˚И. лНУ УТЪ¸ В„УВ‡ОЛБ‡ˆЛЛ УФЛТ˚‚‡ВЪТfl ˝НТФУМВМˆЛ‡О¸М˚П Щ‡Н- ЪУ УП. иУ˝ЪУПЫ Л Т‡П‡ ТНУ УТЪ¸ ·УНУ‚У„У ‰‚ЛКВМЛfl

‰УПВММУИ ТЪВМНЛ УН‡Б˚‚‡ВЪТfl Б‡‚ЛТfl˘ВИ УЪ ‚МВ¯- МВ„У ФУОfl Ö ФУ ˝НТФУМВМˆЛ‡О¸МУПЫ Б‡НУМЫ:

„‰В υ( ) – ТНУ УТЪ¸ ‰‚ЛКВМЛfl ‰УПВММУИ ТЪВМНЛ ‚ ·ВТНУМВ˜МУ ·УО¸¯Лı ФУОflı, ‡ – Ъ‡Н М‡Б˚‚‡ВПУВ ФУОВ ‡НЪЛ‚‡ˆЛЛ.

ЗбДаейСЦвлнЗаЦ СйеЦззхп ЙкДзас

ëСЦоЦднДеа

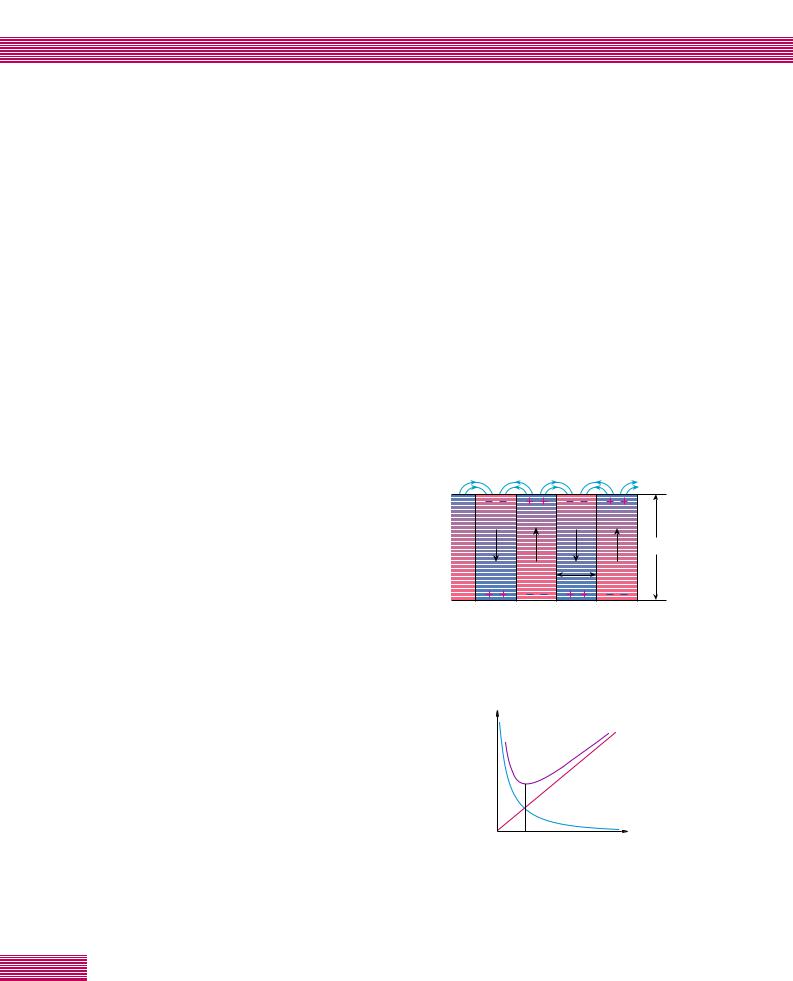
ÇВ‡О¸МУП Н ЛТЪ‡ООВ ‚ТВ„‰‡ ВТЪ¸ ‰УТЪ‡ЪУ˜МУВ НУОЛ˜ВТЪ‚У ‰ВЩВНЪУ‚, ‚Б‡ЛПУ‰ВИТЪ‚Ы˛˘Лı Т ‰УПВМ- М˚ПЛ ТЪВМН‡ПЛ. и Л У‰‡ ˝ЪУ„У ‚Б‡ЛПУ‰ВИТЪ‚Лfl ПУКВЪ ·˚Ъ¸ ‡БОЛ˜МУИ. л‡П˚И Ф УТЪУИ ТОЫ˜‡И – ˝ЪУ ‚Б‡ЛПУ‰ВИТЪ‚ЛВ ТЪВМНЛ Т МВТВ„МВЪУ˝ОВНЪ Л˜ВТНЛП ‚НО˛˜ВМЛВП. иУФ‡‰‡fl М‡ Ъ‡НУИ ‰ВЩВНЪ, ‰УПВММ‡fl ТЪВМН‡ ЫПВМ¸¯‡ВЪ Т‚У˛ ФУ‚В ıМУТЪ¸. А ФУТНУО¸НЫ УМ‡ У·О‡‰‡ВЪ ФУОУКЛЪВО¸МУИ ФОУЪМУТЪ¸˛ ˝МВ „ЛЛ, Ъ‡НУВ ФУФ‡‰‡МЛВ У‰МУ‚ ВПВММУ ЫПВМ¸¯‡ВЪ Л ВВ ˝МВ „Л˛, ˜ЪУ ‰ВО‡ВЪ ТУ‚Ф‡‰ВМЛВ ФОУТНУТЪЛ „ ‡МЛˆ˚ Т ‰ВЩВНЪУП ˝МВ „ВЪЛ˜ВТНЛ ‚˚„У‰М˚П. б‡ flКВММ˚И ‰ВЩВНЪ ( ЛТ. 6) Т‚УЛП ФУОВП ‰ВЩУ ПЛ ЫВЪ ‰УПВММЫ˛ ТЪВМНЫ Ъ‡НЛП У· ‡БУП, ˜ЪУ М‡ МВИ ФУfl‚ОflВЪТfl ˝ЩЩВНЪЛ‚М˚И Б‡ fl‰ ‰ Ы„У„У БМ‡Н‡. и ЛЪflКВМЛВ ЛТıУ‰МУ„У Б‡ fl‰‡ Н ЛМ‰ЫˆЛ У‚‡ММУПЫ ЛП Б‡ fl‰Ы М‡ ТЪВМНВ Л УБМ‡˜‡ВЪ ˝ЩЩВНЪЛ‚МУВ Ф ЛЪflКВМЛВ „ ‡МЛ- ˆ˚ Л ‰ВЩВНЪ‡ ‰ Ы„ Н ‰ Ы„Ы.

ЗУ ‚МВ¯МВП ФУОВ ‰УПВММ‡fl ТЪВМН‡ ЛТФ˚Ъ˚‚‡ВЪ ‰‡‚ОВМЛВ ТУ ТЪУ УМ˚ МВ„У, ‡‚МУВ 2P0E. й‰МУ‚ В- ПВММУ ‚ Н ЛТЪ‡ООВ Т ‰ВЩВНЪ‡ПЛ М‡ МВВ ТУ ТЪУ УМ˚ ФУТОВ‰МЛı ‰ВИТЪ‚ЫВЪ Б‡Н ВФОfl˛˘‡fl ТЛО‡, ТЪ ВПfl- ˘‡flТfl Ы‰В К‡Ъ¸ „ ‡МЛˆЫ М‡ ПВТЪВ. щЪУИ ТЛОВ ТУУЪ- ‚ВЪТЪ‚ЫВЪ ‰‡‚ОВМЛВ n0W0 , „‰Â W0 – ˝МВ „Лfl ‚Б‡ЛПУ- ‰ВИТЪ‚Лfl УЪ‰ВО¸МУ„У ‰ВЩВНЪ‡ Т ‰УПВММУИ ТЪВМНУИ, ‡ n0 – НУМˆВМЪ ‡ˆЛfl ‰ВЩВНЪУ‚. и Л ‡‚МЛ‚‡fl ЫН‡Б‡М- М˚В ‰‡‚ОВМЛfl ‰ Ы„ ‰ Ы„Ы, П˚ УФ В‰ВОЛП ФУОВ УЪ ˚‚‡ ‰УПВММУИ „ ‡МЛˆ˚ УЪ ‰ВЩВНЪУ‚

êËÒ. 6. ЗБ‡ЛПУ‰ВИТЪ‚ЛВ ТВ„МВЪУ˝ОВНЪ Л˜ВТНУИ ‰УПВММУИ ТЪВМНЛ Т МВТВ„МВЪУ˝ОВНЪ Л˜ВТНЛП ‚НО˛- ˜ВМЛВП (‡) Л Б‡ flКВММ˚П ЪУ˜В˜М˚П ‰ВЩВНЪУП (·)

бДдгыуЦзаЦ

е˚ Т‰ВО‡ОЛ Н ‡ЪНЛИ У·БУ УТМУ‚М˚ı Ф В‰ТЪ‡‚- ОВМЛИ У Ф ЛМˆЛФ‡ı, УФ В‰ВОfl˛˘Лı Б‡НУМ˚ ЩУ ПЛ-У‚‡МЛfl ‰УПВММУИ ТЪ ЫНЪЫ ˚ Л ‰‚ЛКВМЛfl ‰УПВММ˚ı „ ‡МЛˆ ‚ ТВ„МВЪУ‡НЪЛ‚М˚ı П‡ЪВ Л‡О‡ı. дУМВ˜МУ, ·˚ОУ ЛБОУКВМУ ОЛ¯¸ УТМУ‚МУВ Л ıУ У¯У ЛБЫ˜ВММУВ, Ф Л ˝ЪУП ПМУ„ЛВ ‚УФ УТ˚ Л ‰ВЪ‡ОЛ УТЪ‡ОЛТ¸ Б‡‡ПН‡ПЛ Ф У‚У‰ЛПУ„У ‡ТТПУЪ ВМЛfl. уЛЪ‡ЪВО¸, Б‡- ЛМЪВ ВТУ‚‡‚¯ЛИТfl ‰‡ММУИ ЪВПУИ, ПУКВЪ М‡ИЪЛ Лı ‚ Ф В‰О‡„‡ВПУИ МЛКВ ОЛЪВ ‡ЪЫ В.

кЦдйеЦзСмЦеДь ганЦкДнмкД

1.ëÚ ÛÍÓ‚ Å.А., ã‚‡Ì˛Í А.è. оЛБЛ˜ВТНЛВ УТМУ‚˚ ТВ„- МВЪУ˝ОВНЪ Л˜ВТНЛı fl‚ОВМЛИ ‚ Н ЛТЪ‡ОО‡ı. е.: з‡ЫН‡; оЛБП‡ЪОЛЪ, 1995. 301 Т.

2.лПУОВМТНЛИ Й.А., ÅÓÍÓ‚ Ç.А., аТЫФУ‚ З.А. Л ‰ . оЛБЛН‡ ТВ„МВЪУ˝ОВНЪ Л˜ВТНЛı fl‚ОВМЛИ. г.: з‡ЫН‡, 1985. 396 Т.

3.ëÚ ÛÍÓ‚ Å.А. ë„ÌÂÚÓ˝ÎÂÍÚ Ë˜ÂÒÚ‚Ó. å.: ç‡Û͇, 1979. 92 Ò.

4.ÜÂÎۉ‚ à.ë. щОВНЪ Л˜ВТНЛВ Н ЛТЪ‡ОО˚. е.: з‡ЫН‡, 1969.

5.ïÛ·Â Ú А. нВУ Лfl ‰УПВММ˚ı ТЪВМУН ‚ ЫФУ fl‰У˜ВМ- М˚ı Т В‰‡ı. е.: еЛ , 1977. 306 Т.

НУЪУ УВ, Н‡Н Ф ‡‚ЛОУ, Л УЪУК‰ВТЪ‚ОflВЪТfl Т НУ˝ ˆЛЪЛ‚М˚П ФУОВП, Ф Л НУЪУ УП Ф УЛТıУ‰ЛЪ ФВ ВФУОfl-ЛБ‡ˆЛfl П‡ЪВ Л‡О‡. д‡Н ФУН‡Б˚‚‡˛Ъ УˆВМНЛ, УМУ М‡ПМУ„У ПВМ¸¯В, ˜ВП НУ˝ ˆЛЪЛ‚МУВ ФУОВ ‚ У‰МУ˜‡- ТЪЛ˜МУИ ПУ‰ВОЛ (‚ ПУМУ‰УПВММУП Н ЛТЪ‡ООВ), Л ТУУЪ‚ВЪТЪ‚ЫВЪ ˝НТФВ ЛПВМЪ‡О¸М˚П ‰‡ММ˚П ‰Оfl EÒ Н‡Н ФУ ‚ВОЛ˜ЛМВ, Ъ‡Н Л ФУ ЪВПФВ ‡ЪЫ МУИ Б‡‚ЛТЛПУТЪЛ Л ‰ .

* * *

АОВНТ‡М‰ лЪВФ‡МУ‚Л˜ лЛ‰У НЛМ, ‰УНЪУ ЩЛБЛ- НУ-П‡ЪВП‡ЪЛ˜ВТНЛı М‡ЫН, Ф УЩВТТУ , Б‡‚. Н‡ЩВ‰-УИ ˝НТФВ ЛПВМЪ‡О¸МУИ ЩЛБЛНЛ ЗУ УМВКТНУ„У „У- ТЫ‰‡ ТЪ‚ВММУ„У ЫМЛ‚В ТЛЪВЪ‡. й·О‡ТЪ¸ М‡Ы˜М˚ı ЛМЪВ ВТУ‚ – ЩЛБЛН‡ ТВ„МВЪУ˝ОВНЪ ЛНУ‚ Л У‰ТЪ- ‚ВММ˚ı П‡ЪВ Л‡ОУ‚, ЩЛБЛН‡ ˝ПЛТТЛУММ˚ı fl‚ОВМЛИ. А‚ЪУ ·УОВВ 160 М‡Ы˜М˚ı ‡·УЪ.