Современные проблемы физики / PhysicalReviewpdf / Delone-1

THE TUNNEL EFFECT

N. B. DELONE

The tunneling of an electron through a potential barrier is, in essence, the basic quantum mechanical effect, which has no analogy in classical mechanics. The tunnel effect is an experimental confirmation of one of the fundamental initial positions of quantum mechanics, which is corpuscular-wave dualism of elementary particles’ properties.

нЫММВОЛ У‚‡МЛВ ˝ОВНЪ УМ‡ ˜В ВБ ФУЪВМˆЛ- ‡О¸М˚И ·‡ ¸В fl‚ОflВЪТfl Ф ЛМˆЛФЛ‡О¸МУ Н‚‡МЪУ‚У-ПВı‡МЛ˜ВТНЛП ˝ЩЩВНЪУП, НУЪУ-˚И МВ ЛПВВЪ ‡М‡ОУ„‡ ‚ НО‡ТТЛ˜ВТНУИ ПВı‡- МЛНВ. нЫММВО¸М˚И ˝ЩЩВНЪ fl‚ОflВЪТfl ˝НТФВ-ЛПВМЪ‡О¸М˚П ФУ‰Ъ‚В К‰ВМЛВП У‰МУ„У ЛБ ЩЫМ‰‡ПВМЪ‡О¸М˚ı ЛТıУ‰М˚ı ФУОУКВМЛИ Н‚‡МЪУ‚УИ ПВı‡МЛНЛ – НУ ФЫТНЫОfl МУ-‚УО- МУ‚У„У ‰Ы‡ОЛБП‡ Т‚УИТЪ‚ ˝ОВПВМЪ‡ М˚ı ˜‡- ТЪЛˆ.

©СВОУМВ з.Е., 2000

1. ЗЗЦСЦзаЦ

нЫММВО¸М˚П ˝ЩЩВНЪУП М‡Б˚‚‡ВЪТfl ‚УБПУКМУТЪ¸ ˝ОВПВМЪ‡ МУИ ˜‡ТЪЛˆВ, М‡Ф ЛПВ ˝ОВНЪ УМЫ, Ф УИЪЛ (Ф У- ЪЫММВОЛ У‚‡Ъ¸) ˜В ВБ ФУЪВМˆЛ‡О¸М˚И ·‡ ¸В , НУ„‰‡ ·‡-¸В ‚˚¯В ФУОМУИ ˝МВ „ЛЛ ˜‡ТЪЛˆ˚. ЗУБПУКМУТЪ¸ ТЫ˘ВТЪ‚У‚‡МЛfl ЪЫММВО¸МУ„У ˝ЩЩВНЪ‡ ‚ ПЛН УПЛ В ·˚- О‡ ФУМflЪ‡ ЩЛБЛН‡ПЛ ‚ ФВ ЛУ‰ ТУБ‰‡МЛfl Н‚‡МЪУ‚УИ ПВ- ı‡МЛНЛ, ‚ 20–30-ı „У‰‡ı М‡¯В„У ‚ВН‡. З ‰‡О¸МВИ¯ВП Б‡ Т˜ВЪ ЪЫММВО¸МУ„У ˝ЩЩВНЪ‡ ·˚ОЛ У·˙flТМВМ˚ МВНУЪУ ˚В ‚ВТ¸П‡ ‚‡КМ˚В fl‚ОВМЛfl, У·М‡ ЫКВММ˚В ˝НТФВ ЛПВМ- Ъ‡О¸МУ ‚ ‡БОЛ˜М˚ı У·О‡ТЪflı ЩЛБЛНЛ.

нЫММВО¸М˚И ˝ЩЩВНЪ fl‚ОflВЪТfl Ф ЛМˆЛФЛ‡О¸МУ Н‚‡МЪУ‚У-ПВı‡МЛ˜ВТНЛП ˝ЩЩВНЪУП, МВ ЛПВ˛˘ЛП ‡М‡- ОУ„‡ ‚ НО‡ТТЛ˜ВТНУИ ПВı‡МЛНВ. З ˝ЪУП УТМУ‚МУИ ЛМЪВ-ВТ ЪЫММВО¸МУ„У ˝ЩЩВНЪ‡ ‰Оfl ЩЛБЛНЛ Л ЩЛБЛНУ‚. З‡ПН‡ı НО‡ТТЛ˜ВТНУИ ПВı‡МЛНЛ ‡Ф ЛУ МУ flТМУ, ˜ЪУ О˛·УВ П‡ЪВ Л‡О¸МУВ ЪВОУ, ЛПВ˛˘ВВ ˝МВ „Л˛ E, МВ ПУКВЪ Ф ВУ‰УОВЪ¸ ФУЪВМˆЛ‡О¸М˚И ·‡ ¸В ‚˚ТУЪУИ V0 , ÂÒÎË V0 > E ( ËÒ. 1, ‡). и Л Ф‡‰ВМЛЛ ЪВО‡ М‡ Ъ‡НУИ ·‡ ¸В УМУ ПУКВЪ ОЛ¯¸ УЪ ‡БЛЪ¸Тfl УЪ МВ„У. щЪУ ЫЪ‚В К‰ВМЛВ М‡ıУ‰ЛЪТfl ‚ ФУОМУП ТУ„О‡ТЛЛ Т Б‡НУМУП ТУı ‡МВМЛfl ˝МВ „ЛЛ.

й‰М‡НУ ВТОЛ ‚ Н‡˜ВТЪ‚В П‡ЪВ Л‡О¸МУ„У ЪВО‡ ‡Т- ТПУЪ ВЪ¸ ˝ОВНЪ УМ, ЪУ МВО¸Бfl УТЪ‡‚‡Ъ¸Тfl ‚ ‡ПН‡ı НО‡Т- ТЛ˜ВТНУИ ПВı‡МЛНЛ. СВИТЪ‚ЛЪВО¸МУ, ıУ У¯У ЛБ‚ВТЪМУ, ˜ЪУ ˝ОВНЪ УМЫ Ф ЛТЫ˘Л Н‡Н НУ ФЫТНЫОfl М˚В, Ъ‡Н Л ‚УОМУ‚˚В Т‚УИТЪ‚‡. СОЛМ‡ ‚УОМ˚ ‰В Е УИОfl ‰Оfl П‡ЪВ Л- ‡О¸МУ„У ЪВО‡ Т П‡ТТУИ m Л ТНУ УТЪ¸˛ υ УФЛТ˚‚‡ВЪТfl ТУУЪМУ¯ВМЛВП

„‰Â " = h/(2π), ‡ h – ФУТЪУflММ‡fl иО‡МН‡. ЦТОЛ П‡ТТ‡ m ˝НТЪ ВП‡О¸МУ П‡О‡ Л ТНУ УТЪ¸ υ МВ˝НТЪ ВП‡О¸МУ ‚В- ОЛН‡, ЪУ ‰ОЛМ‡ ‚УОМ˚ ‰В Е УИОfl ПУКВЪ ·˚Ъ¸ МВП‡О‡. н‡Н, М‡Ф ЛПВ , ‰Оfl ˝ОВНЪ УМ‡, ЛПВ˛˘В„У НЛМВЪЛ˜ВТНЫ˛ ˝МВ „Л˛ ФУ fl‰Н‡ 1 ˝З, ‚ВОЛ˜ЛМ‡ λD ÔÓ fl‰Í‡ 10ra10−7 ÒÏ, „‰Â ra – ·Ó Ó‚ÒÍËÈ ‡‰ËÛÒ. Ç ‡ÚÓÏÌ˚ı χүڇ- ·‡ı ˝ÚÓ Ó˜Â̸ ·Óθ¯‡fl ‚Â΢Ë̇ – ̇ ÔÓ fl‰ÓÍ Ô Â‚˚- ¯‡˛˘‡fl ‡ÁÏ ‡ÚÓχ!

ЕЫ‰ВП Ф В‰ФУО‡„‡Ъ¸, ˜ЪУ ФУЪВМˆЛ‡О¸М˚И ·‡ ¸В fl‚- ОflВЪТfl ТЪ‡ˆЛУМ‡ М˚П, Л ЛТıУ‰ЛЪ¸ ЛБ Ы ‡‚МВМЛfl т fi- ‰ЛМ„В ‡ ‚ ЩУ ПВ, МВ Б‡‚ЛТfl˘ВИ УЪ ‚ ВПВМЛ:

ä‡Í ‚ˉÌÓ ËÁ (8), ¯ÂÌË ‚ ˝ÚÓÈ Ó·Î‡ÒÚË Ô Â‰ÒÚ‡‚- ÎflÂÚ ÒÓ·ÓÈ ÓÒˆËÎÎË Û˛˘Û˛ ÙÛÌÍˆË˛, Ì ‚ÓÁ ‡ÒÚ‡˛- ˘Û˛ Ô Ë x − .

Ç (2), Í‡Í Ë ‡ÌÂÂ, E – ÔÓÎ̇fl ˝Ì „Ëfl ˜‡ÒÚˈ˚, V(x) – ФУЪВМˆЛ‡О¸М˚И ·‡ ¸В , 2 – ÓÔ ‡ÚÓ ã‡Ô·҇, ‡

ψ(x, t) – ‚ÓÎÌÓ‚‡fl ÙÛÌ͈Ëfl, ı‡ ‡ÍÚ ËÁÛ˛˘‡fl ‚ ÓflÚ-

ÌÓÒÚ¸ ̇ıÓʉÂÌËfl ˜‡ÒÚˈ˚ ‚ ‰‡ÌÌÓÈ ÚÓ˜ÍÂ.

ЕЫ‰ВП В¯‡Ъ¸ МВ ЛТЪЛММЫ˛ Ъ ВıПВ МЫ˛ Б‡‰‡˜Ы, ‡ У‰МУПВ МЫ˛ Б‡‰‡˜Ы. щЪУ ФУБ‚УОflВЪ Б‡ПВМЛЪ¸ Ы ‡‚МВМЛВ

(2) ‚ ˜‡ТЪМ˚ı Ф УЛБ‚У‰М˚ı М‡ У·˚˜МУВ ‰ЛЩЩВ ВМˆЛ- ‡О¸МУВ Ы ‡‚МВМЛВ Т У‰МУИ МВБ‡‚ЛТЛПУИ ФВ ВПВММУИ x:

ᇂËÒfl˘‡fl ÓÚ ÍÓÓ ‰Ë̇Ú˚ ˜‡ÒÚ¸ ‚ÓÎÌÓ‚ÓÈ ÙÛÌ͈ËË Û‰Ó‚ÎÂÚ‚Ó flÂÚ Û ‡‚ÌÂÌ˲

кВ¯Л‚ Ы ‡‚МВМЛВ (5) УЪМУТЛЪВО¸МУ ϕ(x), ПУКМУ ФУОЫ˜ЛЪ¸ ЛБ (4) ‚˚ ‡КВМЛВ ‰Оfl ЛТНУПУИ ‚УОМУ‚УИ ЩЫМНˆЛЛ ψ(x, t). З Н‡˜ВТЪ‚В ·‡ ¸В ‡ ‚˚·В ВП Ф УТЪВИ¯Ы˛ ТЪЫФВМ˜‡ЪЫ˛ ЩУ ПЫ ( ЛТ. 1, ·):

З‚В‰fl ˝ЪЛ ЫФ У˘ВМЛfl, ФВ ВИ‰ВП Н ‚˚˜ЛТОВМЛ˛ ЩЫМНˆЛЛ ϕ(x) ‰Оfl Ф УЛБ‚УО¸МУ„У БМ‡˜ВМЛfl ‡ „ЫПВМЪ‡. й· ‡- ЪЛПТfl ТМ‡˜‡О‡ Н У·О‡ТЪЛ ТОВ‚‡ УЪ ·‡ ¸В ‡, „‰В x < 0. З ˝ЪУИ У·О‡ТЪЛ Ы ‡‚МВМЛВ (5) Т‚У‰ЛЪТfl Н Ы ‡‚МВМЛ˛

гВ„НУ ЫТЪ‡МУ‚ЛЪ¸, ˜ЪУ ˝ЪУ Ы ‡‚МВМЛВ ЛПВВЪ ‰‚‡ МВБ‡‚Л-

ÍËÏ Ó· ‡ÁÓÏ, ‚ ˝ÚÓÈ Ó·Î‡ÒÚË ‚ÓÎÌÓ‚‡fl ÙÛÌ͈Ëfl ϕ(x) УФЛТ˚‚‡ВЪТfl ‚˚ ‡КВМЛВП

ã„ÍÓ ÔÓÎÛ˜ËÚ¸ ‰‚‡ ÌÂÁ‡‚ËÒËÏ˚ı ¯ÂÌËfl ˝ÚÓ„Ó Û ‡‚ÌÂÌËfl, ÓÌË ËÏÂ˛Ú ‚ˉ

ЗЪУ УВ ЛБ ˝ЪЛı В¯ВМЛИ ˝НТФУМВМˆЛ‡О¸МУ ‡ТЪВЪ ТУТЪУП x, ˜ЪУ, У˜В‚Л‰МУ, ЩЛБЛ˜ВТНЛ ·ВТТП˚ТОВММУ. (з‡ФУПМЛП, ˜ЪУ ЛТıУ‰МУ Ф В‰ФУО‡„‡ВЪТfl, ˜ЪУ ϕ(x) – ‚УОМУ‚‡fl ЩЫМНˆЛfl, ı‡ ‡НЪВ ЛБЫ˛˘‡fl ‚В УflЪМУТЪ¸ М‡- ıУК‰ВМЛfl ˜‡ТЪЛˆ˚.) н‡НЛП У· ‡БУП, УТЪ‡ВЪТfl ОЛ¯¸ ФВ ‚УВ ЛБ В¯ВМЛИ Ы ‡‚МВМЛfl (9) Cexp(−qx), ТУУЪ‚ВЪТЪ- ‚Ы˛˘ВВ ˝НТФУМВМˆЛ‡О¸МУПЫ Ы·˚‚‡МЛ˛ ЩЫМНˆЛЛ ϕ(x) ТУТЪУП ‚ВОЛ˜ЛМ˚ x ‚ ӷ·ÒÚË x > 0.

íÂÔ ¸ ÓÒÚ‡ÂÚÒfl Ò¯ËÚ¸ ¯ÂÌËfl, ÔÓÎÛ˜ÂÌÌ˚ ‰Îfl ӷ·ÒÚÂÈ Ò x < 0 Ë x > 0 ‚ ÚӘ͠x = 0. дУМТЪ‡МЪ˚ A, B Ë C УФ В‰ВОfl˛Ъ ЛТıУ‰fl ЛБ У˜В‚Л‰МУ„У Ф В‰ФУОУКВМЛfl У МВФ В ˚‚МУТЪЛ ‚УОМУ‚УИ ЩЫМНˆЛЛ Л ВВ ФВ ‚УИ Ф УЛБ- ‚У‰МУИ ‚У ‚ТВИ У·О‡ТЪЛ ЛБПВМВМЛfl ‚ВОЛ˜ЛМ˚ x.

йНУМ˜‡ЪВО¸МУВ ‚˚ ‡КВМЛВ ‰Оfl ЩЫМНˆЛЛ ϕ(x) ЛПВВЪ

‚ˉ

(·ВБ У„ ‡МЛ˜ВМЛfl У·˘МУТЪЛ ПУКМУ ФУОУКЛЪ¸ A = 1). àÁ ‚˚ ‡ÊÂÌËfl (10) ‚ˉÌÓ, ˜ÚÓ Ô Ë x < 0 ÙÛÌ͈Ëfl

ϕ(x) Ô Â‰ÒÚ‡‚ÎflÂÚ ÒÓ·ÓÈ ÒÛÔ ÔÓÁËˆË˛ ‰‚Ûı ‚ÓÎÌ. é‰Ì‡ ËÁ ‚ÓÎÌ, exp(ikx), ‡ÒÔ ÓÒÚ ‡ÌflÂÚÒfl ‚Ô ‡‚Ó, ‚ ÒÚÓ ÓÌÛ ·‡ ¸Â ‡; ‚ÚÓ ‡fl, exp(−ikx), – ‚ОВ‚У УЪ ·‡ ¸В ‡. н‡Н Н‡Н ПУ‰ЫО¸ ПМУКЛЪВОfl Ф Л exp(ikx) ‚ ‚˚ ‡КВМЛЛ (10) ‡- ‚ВМ 1, ЪУ ‡ПФОЛЪЫ‰˚ ˝ЪЛı ‚УОМ ‡‚М˚. н‡НЛП У· ‡БУП, ТОВ‚‡ УЪ ·‡ ¸В ‡, Ф Л x < 0, ‚˚ ‡КВМЛВ (8) УФЛТ˚‚‡ВЪ ˜‡ТЪЛˆЫ, Ф‡‰‡˛˘Ы˛ М‡ ·‡ ¸В Л ЫФ Ы„У УЪ ‡К‡˛˘Ы˛Тfl ( ЛТ. 1, ·). щЪУЪ Ф УˆВТТ ТУУЪ‚ВЪТЪ‚ЫВЪ Ф В‰ТН‡Б‡МЛflП НО‡ТТЛ˜ВТНУИ ПВı‡МЛНЛ.

é‰Ì‡ÍÓ ËÁ ‚˚ ‡ÊÂÌËfl (10) Ú‡ÍÊ ‚ˉÌÓ, ˜ÚÓ Ô Ë x > 0 ‚УОМУ‚‡fl ЩЫМНˆЛfl Ф УМЛН‡ВЪ Б‡ ·‡ ¸В ‚ У·О‡ТЪ¸, Б‡Ф В- ˘ВММЫ˛ Т ЪУ˜НЛ Б ВМЛfl НО‡ТТЛ˜ВТНУИ ПВı‡МЛНЛ. АПФОЛЪЫ‰‡ ‚УОМУ‚УИ ЩЫМНˆЛЛ Б‡ ·‡ ¸В УП ˝НТФУМВМˆЛ‡О¸МУ ЫПВМ¸¯‡ВЪТfl Ф Л Ы‚ВОЛ˜ВМЛЛ x, Ë Ô Ë ·Óθ¯Ëı x УМ‡ ТЪ ВПЛЪТfl Н МЫО˛ ( ЛТ. 1, ·):

н‡НЛП У· ‡БУП, ТФ ‡‚‡ УЪ ·‡ ¸В ‡ ‚˚ ‡КВМЛВ (10) УФЛТ˚‚‡ВЪ ЪЫММВОЛ У‚‡МЛВ ˜‡ТЪЛˆ˚ ‚ НО‡ТТЛ˜ВТНЛ Б‡- Ф В˘ВММЫ˛ У·О‡ТЪ¸.

аБ ‚˚ ‡КВМЛfl (10) Ъ‡НКВ ПУКМУ ‚Л‰ВЪ¸, ˜ЪУ Ф Л МВУ„ ‡МЛ˜ВММУ ·УО¸¯УИ ‚˚ТУЪВ ·‡ ¸В ‡ (V0 ) ‚Â- ΢Ë̇ q ТЪ ВПЛЪТfl Н ·ВТНУМВ˜МУТЪЛ. лУ„О‡ТМУ (10), ˝ЪУ УБМ‡˜‡ВЪ, ˜ЪУ ‚ВОЛ˜ЛМ‡ ϕ(x) = 0 Ô Ë x > 0. н‡НЛП У·-‡БУП, Ф Л ·ВТНУМВ˜МУИ ‚˚ТУЪВ ·‡ ¸В ‡ П˚ ‚УБ‚ ‡˘‡- ВПТfl Н НО‡ТТЛ˜ВТНУИ Н‡ ЪЛМВ – ˜‡ТЪЛˆ‡ Б‡ ·‡ ¸В МВ Ф УМЛН‡ВЪ, ‡ ОЛ¯¸ УЪ ‡К‡ВЪТfl УЪ МВ„У. щЪУ ФУ‰Ъ‚В К‰‡- ВЪ, ˜ЪУ Н‚‡МЪУ‚‡fl Н‡ ЪЛМ‡ Ф Л МВ·ВТНУМВ˜МУ ‚˚ТУНУП ·‡ ¸В В ‚ФУОМВ ‡БЫПМ‡.

З ЪУП ТОЫ˜‡В, НУ„‰‡ ·‡ ¸В ЛПВВЪ НУМВ˜МЫ˛ ¯Л ЛМЫ R Ë ‰ÓÒÚ‡ÚÓ˜ÌÓ ÛÁÓÍ, Ú‡Í ˜ÚÓ R # λD , ˜‡ТЪЛˆ‡ ЪЫММВОЛ-ЫВЪ Б‡ ·‡ ¸В Т УФ В‰ВОВММУИ ‚В УflЪМУТЪ¸˛ Л ϕ2(x > R)‡ÒÔ ÓÒÚ ‡ÌflÂÚÒfl ‚Ô ‡‚Ó ‚ Ô ÓÒÚ ‡ÌÒÚ‚Â Á‡ ·‡ ¸Â ÓÏ ( ËÒ. 1, ‚). и Л ˝ЪУП ТЫПП‡ ‚В УflЪМУТЪВИ Ф УЪЫММВОЛ-У‚‡Ъ¸ ˜В ВБ ·‡ ¸В Л УЪ ‡БЛЪ¸Тfl УЪ МВ„У ‡‚М‡ В‰ЛМЛˆВ. лУУЪ‚ВЪТЪ‚ВММУ ‡ПФОЛЪЫ‰‡ ‚УОМ˚, УЪ ‡КВММУИ УЪ ·‡ ¸В ‡, ПВМ¸¯В ‡ПФОЛЪЫ‰˚ ‚УОМ˚, Ф‡‰‡˛˘ВИ М‡ ·‡ ¸- В . З ТУУЪ‚ВЪТЪ‚ЛЛ Т ЩУ ПЫОУИ (11) ‚В УflЪМУТЪ¸ ЪЫММВОЛ У‚‡МЛfl ˝НТФУМВМˆЛ‡О¸МУ П‡О‡, ВТОЛ ·‡ ¸В МВ˝НТЪ-ВП‡О¸МУ ЫБУН.

дУМН ВЪМ‡fl ЩУ П‡ ·‡ ¸В ‡ (НУЪУ ˚И В‡О¸МУ МЛНУ„‰‡ МВ ·˚‚‡ВЪ Ф flПУЫ„УО¸М˚П) ЛБПВМflВЪ НУОЛ˜ВТЪ- ‚ВММУ ‚В УflЪМУТЪ¸ ЪЫММВОЛ У‚‡МЛfl, МВ ЛБПВМflfl ЪУИ Н‡˜ВТЪ‚ВММУИ Н‡ ЪЛМ˚, НУЪУ ‡fl ФУОЫ˜ВМ‡ ‚˚¯В.

н‡НЛП У· ‡БУП, Б‡‰‡˜‡, ФУТЪ‡‚ОВММ‡fl ‚ М‡˜‡ОВ ˝ЪУ- „У ‡Б‰ВО‡, ‚˚ФУОМВМ‡ ‚ ‡ПН‡ı Н‚‡МЪУ‚УИ ПВı‡МЛНЛ: ФУН‡Б‡МУ ТЫ˘ВТЪ‚У‚‡МЛВ ЪЫММВО¸МУ„У ˝ЩЩВНЪ‡, Ф Л‚У- ‰fl˘В„У Н Ф УМЛНМУ‚ВМЛ˛ ˜‡ТЪЛˆ˚ Б‡ ·‡ ¸В , ‚˚ТУЪ‡ НУЪУ У„У ·УО¸¯В ˝МВ „ЛЛ ˜‡ТЪЛˆ˚. кВ¯ВМЛВ ˝ЪУИ Б‡‰‡- ˜Л ·ВБ ЪВı ЫФ У˘ВМЛИ, НУЪУ ˚В ·˚ОЛ Т‰ВО‡М˚ ‚˚¯В, ФУН‡Б˚‚‡ВЪ, ˜ЪУ ВБЫО¸Ъ‡Ъ Н‡˜ВТЪ‚ВММУ МВ УЪОЛ˜‡ВЪТfl УЪ ФУОЫ˜ВММУ„У ‚˚¯В.

аБ-Б‡ МВ‰УТЪ‡ЪН‡ ПВТЪ‡ П˚ МВ ‡ТТП‡Ъ Л‚‡ВП Б‰ВТ¸ Ф УˆВТТ М‡‰·‡ ¸В МУ„У УЪ ‡КВМЛfl ˜‡ТЪЛˆ. ЬВО‡˛˘ЛВ‡БУ· ‡Ъ¸Тfl ‚ МВП ПУ„ЫЪ У· ‡ЪЛЪ¸Тfl Н ЫФУПflМЫЪУПЫ‡М¸¯В НЫ ТЫ Н‚‡МЪУ‚УИ ПВı‡МЛНЛ [2].

иВ ВИ‰ВП ЪВФВ ¸ Н Н ‡ЪНУПЫ ‡ТТПУЪ ВМЛ˛ fl‰‡ УТМУ‚М˚ı ЩЛБЛ˜ВТНЛı fl‚ОВМЛИ, ‚ НУЪУ ˚ı В‡ОЛБЫВЪТfl ЪЫММВО¸М˚И ˝ЩЩВНЪ.

3. оабауЦлдаЦ ьЗгЦзаь, йЕмлгйЗгЦззхЦ нмззЦгъзхе щооЦднйе

α-ê‡ÒÔ‡‰ ‡ÚÓÏÌ˚ı fl‰Â

ь‚ОВМЛВ ‡‰ЛУ‡НЪЛ‚МУТЪЛ ·˚ОУ У·М‡ ЫКВМУ А. ЕВННВ В- ОВП ‚ Т‡ПУП НУМˆВ XIX ‚ВНВ. йМ ЫТЪ‡МУ‚ЛО, ˜ЪУ ‡ЪУПМ˚В fl‰ ‡ ТФУМЪ‡ММУ (Т‡ПУФ УЛБ‚УО¸МУ) ЛТФЫТН‡˛Ъ α-, β- Л

γ-ОЫ˜Л, ı‡ ‡НЪВ ЛБЫВП˚В ‡БОЛ˜МУИ Ф УМЛН‡˛˘ВИ ТФУТУ·МУТЪ¸˛. ЗТНУ В ФУТОВ ˝ЪУ„У щ. кВБВ ЩУ ‰ Л е. д˛ Л ЫТЪ‡МУ‚ЛОЛ, ˜ЪУ ˝ЪУ α-˜‡ТЪЛˆ˚ (fl‰ ‡ „ВОЛfl), ˝ОВНЪ УМ˚ Л γ-ОЫ˜Л. З М‡˜‡ОВ XX ‚ВН‡ ·˚О М‡НУФОВМ БМ‡˜ЛЪВО¸М˚И ˝НТФВ ЛПВМЪ‡О¸М˚И П‡ЪВ Л‡О У Т‚УИТЪ‚‡ı ‡‰ЛУ‡НЪЛ‚- МУТЪЛ fl‰В . З ˜‡ТЪМУТЪЛ, ·˚ОЛ ЛБПВ ВМ˚ ФВ ЛУ‰˚ ФУОЫ ‡ТФ‡‰‡ fl‰В Л ˝МВ „ЛЛ ‚˚ОВЪ‡˛˘Лı ˜‡ТЪЛˆ Л γ-ОЫ- ˜ВИ. щЪЛ ‰‡ММ˚В ‰Оfl α-˜‡ТЪЛˆ УН‡Б‡ОЛТ¸ М‡ ФВ ‚˚И ‚Б„Оfl‰ МВУКЛ‰‡ММ˚ПЛ. н‡Н, Т У‰МУИ ТЪУ УМ˚, ˝МВ „ЛЛ ‚˚ОВЪ‡˛˘Лı α-˜‡ТЪЛˆ ‰Оfl ·УО¸¯У„У ˜ЛТО‡ ‡БОЛ˜М˚ı fl‰В УН‡Б‡ОЛТ¸ ФУ˜ЪЛ У‰ЛМ‡НУ‚˚ПЛ. л ‰ Ы„УИ – ФВ ЛУ- ‰˚ ФУОЫ ‡ТФ‡‰‡ ˝ЪЛı КВ fl‰В – ‡БОЛ˜‡ОЛТ¸ М‡ ПМУ„У ФУ fl‰НУ‚ ‚ВОЛ˜ЛМ˚. н‡Н, М‡Ф ЛПВ , ‰Оfl α- ‡ТФ‡‰‡ fl‰ ‡ ФУОУМЛfl 21292Po Ô ËÓ‰ ÔÓÎÛ ‡ÒÔ‡‰‡ ÔÓ fl‰Í‡ 10−7 Ò, ‡ ‚ ÒÎÛ˜‡Â fl‰ ‡ Û ‡Ì‡ 23892U – ÔÓ fl‰Í‡ 109 ОВЪ. щЪУЪ Ф‡ ‡‰УНТ М‡¯ВО У·˙flТМВМЛВ ОЛ¯¸ ‚ ‡ПН‡ı ЪВУ ЛЛ ЪЫММВОЛ У‚‡- МЛfl ‚˚ОВЪ‡˛˘Лı α-˜‡ТЪЛˆ ˜В ВБ ФУЪВМˆЛ‡О¸М˚И ·‡ ¸- В , У·˙flТМЛ‚¯ЛИ Л Т‡П Щ‡НЪ α- ‡ТФ‡‰‡ fl‰В .

нЫММВО¸М‡fl ЪВУ Лfl α- ‡ТФ‡‰‡ ·˚О‡ ТУБ‰‡М‡ ‚ 20-ı „У‰‡ı ˝ЪУ„У ‚ВН‡ МВБ‡‚ЛТЛПУ Й.А. Й‡ПУ‚˚П, ‡ Ъ‡НКВ к. ЙВ - МЛ Л Ц. дУМ‰УМУП. йМ‡ ‡М‡ОУ„Л˜М‡ ЪВУ ВЪЛ˜ВТНУПЫ УФЛ- Т‡МЛ˛ ЪЫММВО¸МУ„У ˝ЩЩВНЪ‡, Ф Л‚В‰ВММУПЫ ‚˚¯В, ‚‡Б‰ВОВ 2.

з‡ ЛТ. 2 Ф Л‚В‰ВМ‡ ТıВП‡ ЪЫММВОЛ У‚‡МЛfl α-˜‡Т- ЪЛˆ˚ ЛБ fl‰ ‡. ЗМЫЪ Л fl‰ ‡ Ф Л r < R, „‰Â R – ‡‰ËÛÒ fl‰ ‡, ̇ α-˜‡ÒÚËˆÛ ‰ÂÈÒÚ‚Û˛Ú fl‰Â Ì˚ ÒËÎ˚ Ô ËÚflÊÂÌËfl, ‚Ì fl‰ ‡ Ô Ë r > R – ТЛО˚ НЫОУМУ‚ТНУ„У УЪЪ‡ОНЛ- ‚‡МЛfl УЪ fl‰ ‡. н‡НЛП У· ‡БУП, ‚ У·О‡ТЪЛ r R ЛПВВЪТfl ФУЪВМˆЛ‡О¸М˚И ·‡ ¸В . З˚ТУЪ‡ ·‡ ¸В ‡ (‚ ТОЫ˜‡В ЪflКВ- О˚ı fl‰В Т ˜ЛТОУП МЫНОУМУ‚ ·УО¸¯В ТЪ‡) V ≈ 25–30 å˝Ç,

‡ ˝Ì „Ëfl α-˜‡ÒÚˈ˚ E ≈ 5–10 å˝Ç. óÂÏ ÏÂ̸¯Â V Ë ·Óθ¯Â E, ЪВП ·УО¸¯В Ф УМЛˆ‡ВПУТЪ¸ ·‡ ¸В ‡ ‰Оfl α-˜‡ТЪЛˆ Л ЪВП ПВМ¸¯В ФВ ЛУ‰ ФУОЫ ‡ТФ‡‰‡ fl‰ ‡. щНТФУМВМˆЛ‡О¸М‡fl Б‡‚ЛТЛПУТЪ¸ Ф УМЛˆ‡ВПУТЪЛ ·‡ ¸В ‡ УЪ ‡БМУТЪЛ V − E (ТП. ‡Б‰ВО 2) У·ЫТОУ‚ОЛ‚‡ВЪ ВБНЛИ‡Б· УТ ФВ ЛУ‰У‚ ФУОЫ ‡ТФ‡‰‡ ‰Оfl ‡БОЛ˜М˚ı fl‰В .

êËÒ. 2. α-ê‡ÒÔ‡‰ fl‰ ‡ ‡ÚÓχ: O – ˆÂÌÚ fl‰ ‡, R – ‡- ‰ËÛÒ fl‰ ‡, OR – ӷ·ÒÚ¸ ‰ÂÈÒÚ‚Ëfl fl‰Â Ì˚ı ÒËÎ Ô Ë- ÚflÊÂÌËfl, r > R – У·О‡ТЪ¸ НЫОУМУ‚ТНУ„У УЪЪ‡ОНЛ‚‡МЛfl α-˜‡ТЪЛˆ˚ УЪ fl‰ ‡, E – ˝Ì „ËË α-˜‡ÒÚˈ˚, V – ‚˚ÒÓ- Ú‡ ·‡ ¸Â ‡

нВУ Лfl Й‡ПУ‚‡ ФУБ‚УОЛО‡ УФЛТ‡Ъ¸ Т ‚ФУОМВ ‡БЫПМУИ ЪУ˜МУТЪ¸˛ ФВ ЛУ‰˚ ‡ТФ‡‰‡ ‡БОЛ˜М˚ı fl‰В ‚У ‚ТВП У„ УПМУП ‰Л‡Ф‡БУМВ Лı ‚ВОЛ˜ЛМ. С‡О¸МВИ¯ЛВ ЫЪУ˜МВМЛfl ˝ЪУИ ЪВУ ЛЛ Ф Л‚ВОЛ ОЛ¯¸ Н МВ·УО¸¯ЛП ФУ- Ф ‡‚Н‡П.

З М‡˜‡ОВ М‡¯В„У ‚ВН‡, ‚ „У‰˚ ТУБ‰‡МЛfl Н‚‡МЪУ‚УИ ПВı‡МЛНЛ, ЫТФВı ЪВУ ЛЛ ЪЫММВОЛ У‚‡МЛfl α-˜‡ТЪЛˆ ЛБ fl‰В УН‡Б‡ОТfl Ы·В‰ЛЪВО¸М˚П ‡ „ЫПВМЪУП ‚ ФУО¸БЫ ТФ ‡- ‚В‰ОЛ‚УТЪЛ УТМУ‚ МУ‚УИ Н‚‡МЪУ‚УИ ЩЛБЛНЛ, Л ‚ ФВ ‚Ы˛ У˜В В‰¸ НУ ФЫТНЫОfl МУ-‚УОМУ‚УИ Ф Л У‰˚ ˝ОВПВМЪ‡ - М˚ı ˜‡ТЪЛˆ.

нЫММВО¸М‡fl ЛУМЛБ‡ˆЛfl ‡ЪУП‡ ФУ‰ ‰ВИТЪ‚ЛВП ‚МВ¯МВ„У ˝ОВНЪ Л˜ВТНУ„У ФУОfl

З М‡˜‡ОВ XX ‚ВН‡ ПМУ„У ˝НТФВ ЛПВМЪУ‚ ·˚ОУ ФУТ‚fl˘В- МУ ЛТТОВ‰У‚‡МЛ˛ ‡ЪУПМ˚ı ТФВНЪ У‚ ФУ„ОУ˘ВМЛfl Л ЛБОЫ˜ВМЛfl. л В‰Л МЛı ·˚ОЛ Л ˝НТФВ ЛПВМЪ˚ ФУ ЛБЫ˜ВМЛ˛ ЛБПВМВМЛИ ТФВНЪ ‡О¸М˚ı ОЛМЛИ ФУ‰ ‰ВИТЪ‚ЛВП ‚МВ¯- МВ„У ФУТЪУflММУ„У ˝ОВНЪ Л˜ВТНУ„У ФУОfl – ˝ЩЩВНЪ тЪ‡ Н‡ [3]. З НУМˆВ 20-ı „У‰У‚ ‚ У‰МУП ЛБ Ъ‡НЛı ˝НТФВ-ЛПВМЪУ‚ к. н ‡Ы·ВМ·В „ ФУОЫ˜ЛО ЩУЪУ„ ‡ЩЛЛ ТФВНЪ-‡О¸М˚ı ОЛМЛИ, М‡ НУЪУ ˚ı ФУ ПВ В Ы‚ВОЛ˜ВМЛfl М‡Ф fl- КВММУТЪЛ ФУОfl М‡·О˛‰‡ОТfl МВ ЪУО¸НУ Т‰‚Л„ ОЛМЛИ, МУ Л Лı Ы¯Л ВМЛВ Л ЛТ˜ВБМУ‚ВМЛВ. ЦТОЛ Т‰‚Л„ М‡ıУ‰ЛОТfl ‚ ТУ„О‡ТЛЛ Т ЪВУ ЛВИ ˝ЩЩВНЪ‡ тЪ‡ Н‡, ЪУ Л Ы¯Л ВМЛВ Л ЛТ˜ВБМУ‚ВМЛВ ОЛМЛИ ‚ ‡ПН‡ı ˝ЪУИ ЪВУ ЛЛ ·˚ОЛ МВУ·˙- flТМЛП˚.

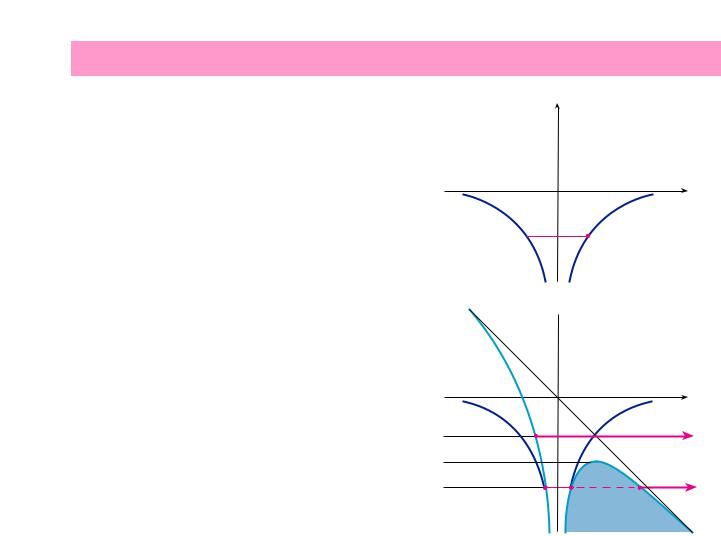
й‰М‡НУ ‚ТНУ В У·‡ ˝ЪЛ fl‚ОВМЛfl ·˚ОЛ У·˙flТМВМ˚ ‚‡ПН‡ı ЪВУ ЛЛ ЪЫММВО¸МУИ Л М‡‰·‡ ¸В МУИ ЛУМЛБ‡ˆЛЛ ‡ЪУПУ‚, ‡Б‚ЛЪУИ МВБ‡‚ЛТЛПУ д. г‡М˜УТУП Л к. йФФВМ- „ВИПВ УП. З УТМУ‚В ˝ЪУИ ЪВУ ЛЛ ОВК‡ОУ Ф В‰ФУОУКВМЛВ, ˜ЪУ ‡ЪУП ФУ‰ ‰ВИТЪ‚ЛВП ‚МВ¯МВ„У ФУОfl ЛУМЛБЫВЪТfl, Ф Л- ˜ВП Ф УˆВТТ ЛУМЛБ‡ˆЛЛ У·ЫТОУ‚ОВМ ‚УБМЛНМУ‚ВМЛВП ФУЪВМˆЛ‡О¸МУ„У ·‡ ¸В ‡, ˜В ВБ НУЪУ ˚И ЪЫММВОЛ ЫВЪ ‡ЪУПМ˚И ˝ОВНЪ УМ. лıВП‡ ˝ЪУ„У Ф УˆВТТ‡ Ф Л‚В‰ВМ‡ М‡ ЛТ. 3.

ÖÒÎË ÌÂÚ ‚̯ÌÂ„Ó ÔÓÎfl ( ËÒ. 3, ‡), ЪУ ˝ОВНЪ УМ, Т‚flБ‡ММ˚И ‚ ‡ЪУПВ, М‡ıУ‰ЛЪТfl ‚ НЫОУМУ‚ТНУП ФУОВ ‡ЪУПМУ„У fl‰ ‡ (Ei – ˝Ì „Ëfl Ò‚flÁË). ÖÒÎË ‚̯Ì ÔÓΠ‚Íβ˜ÂÌÓ (Ì‡Ô ËÏ , ‚‰Óθ ÓÒË z) ( ËÒ. 3, ·), ЪУ М‡ ˝ОВНЪ УМ ‰ВИТЪ‚ЫВЪ ТЫПП‡ ‰‚Ыı ФУОВИ: НЫОУМУ‚ТНУ„У ФУОfl fl‰ ‡ Л ‚МВ¯МВ„У ФУОfl (Т М‡Ф flКВММУТЪ¸˛ F). З˚ТУЪ‡ Л ¯Л ЛМ‡ ˝ЪУ„У ·‡ ¸В ‡ ЫПВМ¸¯‡˛ЪТfl Ф Л Ы‚ВОЛ˜ВМЛЛ М‡Ф flКВММУТЪЛ ‚МВ¯МВ„У ФУОfl. АЪУПМ˚И ˝ОВНЪ УМ ПУКВЪ ЪЫММВОЛ У‚‡Ъ¸ ˜В ВБ ˝ЪУЪ ·‡ ¸В ЛОЛ ‰‡КВ Ф У- ТЪУ УН‡Б˚‚‡ВЪТfl Т‚У·У‰М˚П Ф Л ‰УТЪ‡ЪУ˜МУ МЛБНУП ·‡-¸В В ( ЛТ. 3, ·). З ФУТОВ‰МВП ТОЫ˜‡В Ф УˆВТТ ЛУМЛБ‡- ˆЛЛ Ф ЛМflЪУ М‡Б˚‚‡Ъ¸ М‡‰·‡ ¸В МУИ ЛУМЛБ‡ˆЛВИ ЛОЛ М‡‰·‡ ¸В М˚П ‡Б‚‡ОУП ‡ЪУП‡. ЗВ УflЪМУТЪ¸ W ЪЫММВОЛ У‚‡МЛfl ˝НТФУМВМˆЛ‡О¸МУ Б‡‚ЛТЛЪ УЪ М‡Ф flКВММУТЪЛ F ‚̯ÌÂ„Ó ÔÓÎfl: W exp(−C/F), „‰Â ë – НУМТЪ‡МЪ‡. щЪУ ТУУЪМУ¯ВМЛВ ıУ У¯У УФЛТ˚‚‡ВЪ ˝НТФВ ЛПВМЪ‡О¸- М˚В ‰‡ММ˚В. СОfl Н ЛЪЛ˜ВТНУИ М‡Ф flКВММУТЪЛ ФУОfl,

E

‡

0

z

Ei

V(z) = –e2

·

FE

0

z

Ej

V

Ei

êËÒ. 3. аУМЛБ‡ˆЛfl ‡ЪУП‡ ‚У ‚МВ¯МВП ФУТЪУflММУП ˝ОВНЪ Л˜ВТНУП ФУОВ: ‡ – ‡ЪУП Ф Л УЪТЫЪТЪ‚ЛЛ ‚МВ¯- МВ„У ФУОfl, O – fl‰ Ó ‡ÚÓχ, V – НЫОУМУ‚ТНЛИ ФУЪВМˆЛ- ‡О ‚Б‡ЛПУ‰ВИТЪ‚Лfl ˝ОВНЪ УМ‡ Т fl‰ УП, Ei – ˝Ì „Ëfl ˝ÎÂÍÚ Ó̇, Ò‚flÁ‡ÌÌÓ„Ó ‚ ‡ÚÓÏÂ; · – ‡ЪУП ‚У ‚МВ¯МВП ФУОВ М‡Ф flКВММУТЪ¸˛ F; V – ‚В ¯ЛМ‡ ФУЪВМˆЛ‡О¸МУ- „У ·‡ ¸В ‡, V > Ei – ˝ОВНЪ УМ ЪЫММВОЛ ЫВЪ ˜В ВБ ·‡-¸В . V < Ej – ˝ОВНЪ УМ ФВ ВıУ‰ЛЪ ЛБ Т‚flБ‡ММУ„У ‚ Т‚У·У‰МУВ ТУТЪУflМЛВ М‡‰ ·‡ ¸В УП

Ф Л НУЪУ УИ ‚УБМЛН‡ВЪ М‡‰·‡ ¸В М‡fl ЛУМЛБ‡ˆЛfl, НО‡Т- ТЛ˜ВТН‡fl ЪВУ Лfl ‰‡ВЪ ‚˚ ‡КВМЛВ, ‚˚ЪВН‡˛˘ВВ ЛБ ‡- ‚ВМТЪ‚‡ ˝МВ „ЛЛ Т‚flБЛ ˝ОВНЪ УМ‡ ‚ ‡ЪУПВ Ei (‚ ˜‡ТЪМУТЪЛ, ФУЪВМˆЛ‡О‡ ЛУМЛБ‡ˆЛЛ) Л П‡НТЛПЫП‡ ·‡ ¸В ‡.

йМУ ЛПВВЪ Ф УТЪУИ ‚Л‰: FÍ E2i ⁄ (4Z ), „‰Â Z – Б‡ fl‰ ‡ЪУПМУ„У УТЪУ‚‡. щЪУ ‚˚ ‡КВМЛВ Ф Л·ОЛКВММУ УФЛТ˚-

‚‡ВЪ ‚УБМЛНМУ‚ВМЛВ М‡‰·‡ ¸В МУИ ЛУМЛБ‡ˆЛЛ.

З 60-ı „У‰‡ı ˝ЪУ„У ‚ВН‡ ·˚ОЛ ТУБ‰‡М˚ О‡БВ ˚. З Ы- Н‡ı ˝НТФВ ЛПВМЪ‡ЪУ У‚ УН‡Б‡ОЛТ¸ ˝НТЪ ВП‡О¸МУ ТЛО¸- М˚В Т‚ВЪУ‚˚В ФУОfl, ФУ˝ЪУПЫ ‚УБМЛН У˜В‚Л‰М˚И ЛМЪВ-ВТ ЩЛБЛНУ‚ Н Ф УˆВТТЫ ЪЫММВО¸МУИ ЛУМЛБ‡ˆЛЛ ‡ЪУПУ‚ ‚ ФВ ВПВММУП ˝ОВНЪ УП‡„МЛЪМУП ФУОВ. З УЪОЛ˜ЛВ УЪ ФУТЪУflММУ„У ФУОfl ‚ ФВ ВПВММУП ФУОВ ·‡ ¸В ‚УБМЛН‡ВЪ ФВ ЛУ‰Л˜ВТНЛ ЪУ ТФ ‡‚‡ УЪ fl‰ ‡ ‡ЪУП‡ (Н‡Н ˝ЪУ ЛБУ· ‡- КВМУ М‡ ЛТ. 3, ·), ÚÓ Ò΂‡ Á‡ ‚ ÂÏfl, ‡‚ÌÓ ÔÓÎÓ‚ËÌÂ

Ô ËÓ‰‡ ÔÓÎfl. Ç Ò‚ÂÚÓ‚ÓÏ ÔÓΠ˝ÚÓ Ó˜Â̸ χ·fl ‚Â΢Ë- ̇, ÔÓ fl‰Í‡ 10−15 Т. й˜В‚Л‰МУ, ˜ЪУ ‡ЪУПМ˚И ˝ОВНЪ УМ ‰УОКВМ ЫТФВЪ¸ Ф УЪЫММВОЛ У‚‡Ъ¸ ˜В ВБ ·‡ ¸В Б‡ ПВМ¸- ¯ВВ ‚ ВПfl. нВУ ВЪЛ˜ВТНЛ ·˚ОУ ФУН‡Б‡МУ, ˜ЪУ ЪЫММВО¸- М‡fl ЛУМЛБ‡ˆЛfl ‡ЪУПУ‚ ПУКВЪ Ф УЛТıУ‰ЛЪ¸ Л ‚ Т‚ВЪУ‚УП ФУОВ О‡БВ МУ„У ЛБОЫ˜ВМЛfl [4]. щНТФВ ЛПВМЪ˚, ФУТЪ‡‚- ОВММ˚В ‚ ФУТОВ‰Ы˛˘ЛВ „У‰˚, ФУОМУТЪ¸˛ ФУ‰Ъ‚В ‰ЛОЛ ˝ЪЛ Ф В‰ФУОУКВМЛfl, Л ТВИ˜‡Т ˝ЪУЪ Ф УˆВТТ ‰ВЪ‡О¸МУ ЛБЫ˜ВМ [5].

и УˆВТТ ЪЫММВО¸МУИ ЛУМЛБ‡ˆЛЛ ‡ЪУПУ‚ ‚ ФУОВ О‡- БВ МУ„У ЛБОЫ˜ВМЛfl Ф В‰ТЪ‡‚ОflВЪ ·УО¸¯УИ ЛМЪВ ВТ. СВОУ ‚ ЪУП, ˜ЪУ Ф Л ТУ‚ ВПВММ˚ı Т‚В ıТЛО¸М˚ı ФУОflı О‡- БВ МУ„У ЛБОЫ˜ВМЛfl ТЫ·‡ЪУПМУИ, ‡ЪУПМУИ (Fa 109 З/cП) Л ТЫФВ ‡ЪУПМУИ М‡Ф flКВММУТЪЛ ˝ЪУЪ Ф УˆВТТ fl‚ОflВЪТfl УФ В‰ВОfl˛˘ЛП Ф Л ЛУМЛБ‡ˆЛЛ „‡Б‡ Л ТУБ‰‡МЛЛ ФО‡Б- П˚. З Ъ‡НЛı ТЛО¸М˚ı Т‚ВЪУ‚˚ı ФУОflı ЪЫММВО¸М˚И ˝Щ- ЩВНЪ У·ЫТОУ‚ОЛ‚‡ВЪ Л УЪ ˚‚ ˝ОВНЪ УМУ‚ УЪ ФУОУКЛЪВО¸М˚ı ЛУМУ‚, Ф Л‚У‰fl Н У· ‡БУ‚‡МЛ˛ ‚ „‡БВ ЛУМУ‚ Т ·УО¸¯УИ Н ‡ЪМУТЪ¸˛ Б‡ fl‰‡ Л ·УО¸¯В„У ˜ЛТО‡ Т‚У·У‰- М˚ı ˝ОВНЪ УМУ‚.

4. бАдгыуЦзаЦ

б‡Н‡М˜Л‚‡fl ТЪ‡Ъ¸˛, УТЪ‡ВЪТfl ОЛ¯¸ ЫН‡Б‡Ъ¸ (Б‡ МВ‰УТЪ‡Ъ- НУП ПВТЪ‡) М‡ ‰ Ы„ЛВ ЩЛБЛ˜ВТНЛВ fl‚ОВМЛfl, ‚ НУЪУ ˚ıВ‡ОЛБЫВЪТfl ЪЫММВО¸М˚И ˝ЩЩВНЪ. щЪУ ‚ ФВ ‚Ы˛ У˜В В‰¸ ‡‚ЪУЛУМЛБ‡ˆЛУММ‡fl (ЛОЛ ıУОУ‰М‡fl, ФУОВ‚‡fl) ˝ПЛТТЛfl ˝ОВНЪ УМУ‚ ЛБ ФУ‚В ıМУТЪЛ ПВЪ‡ОО‡ Л ‰ Ы„Лı ˝ОВНЪ У- Ф У‚У‰fl˘Лı Т В‰, ¯Л УНУ ЛТФУО¸БЫВП‡fl ‚ ˝ОВНЪ УМЛНВ.

З ФУОЫФ У‚У‰МЛН‡ı ‚ УФ В‰ВОВММ˚ı ЫТОУ‚Лflı ‚УБМЛН‡ВЪ ЪЫММВО¸М˚И ˝ЩЩВНЪ М‡ p–n-ФВ ВıУ‰В. щЪУ ФУБ- ‚УОЛОУ ТУБ‰‡Ъ¸ ЪЫММВО¸М˚В ‰ЛУ‰˚, ЛПВ˛˘ЛВ ТЫ˘ВТЪ- ‚ВММ˚В Ф ВЛПЫ˘ВТЪ‚‡ ФВ В‰ У·˚˜М˚ПЛ ‰ЛУ‰‡ПЛ ‚ ¯Л ЛМВ ФУОУТ˚ Ф УФЫТН‡ВП˚ı ˜‡ТЪУЪ Л ·˚ТЪ У‰ВИТЪ- ‚ЛЛ. нЫММВО¸М˚И ˝ЩЩВНЪ УФ В‰ВОflВЪ Ф УˆВТТ ПЛ„ ‡- ˆЛЛ ‚‡ОВМЪМ˚ı ˝ОВНЪ УМУ‚ ‚ Н ЛТЪ‡ООЛ˜ВТНУИ В¯ВЪНВ

Ъ‚В ‰˚ı ЪВО. нЫММВО¸М˚И ˝ЩЩВНЪ ОВКЛЪ ‚ УТМУ‚В ˝Щ- ЩВНЪ‡ СКУБВЩТУМ‡ – Ф УЪВН‡МЛfl Т‚В ıФ У‚У‰fl˘В„У ЪУН‡ ПВК‰Ы ‰‚ЫПfl Т‚В ıФ У‚У‰МЛН‡ПЛ ˜В ВБ ˝НТЪ В- П‡О¸МУ ЪУМНЫ˛ Ф УТОУИНЫ ЛБ ‰Л˝ОВНЪ ЛН‡.

аБ Ф Л‚В‰ВММУ„У П‡ЪВ Л‡О‡ ‚Л‰МУ, ˜ЪУ ЪЫММВО¸- М˚И ˝ЩЩВНЪ Л„ ‡ВЪ ТЫ˘ВТЪ‚ВММЫ˛ УО¸ ‚ Т‡П˚ı ‡БОЛ˜- М˚ı У·О‡ТЪflı ЩЛБЛНЛ Л ЪВıМЛНЛ.

й‰М‡НУ М‡Л·УОВВ ¯Л УНЛИ ЛМЪВ ВТ Н ЪЫММВО¸МУПЫ ˝ЩЩВНЪЫ У·ЫТОУ‚ОВМ ЪВП, ˜ЪУ ˝ЪУ Ф ЛМˆЛФЛ‡О¸МУ Н‚‡М- ЪУ‚У-ПВı‡МЛ˜ВТНЛИ ˝ЩЩВНЪ, МВ ЛПВ˛˘ЛИ ‡М‡ОУ„‡ ‚ НО‡ТТЛ˜ВТНУИ ПВı‡МЛНВ. л‚УЛП ТЫ˘ВТЪ‚У‚‡МЛВП ЪЫММВО¸М˚И ˝ЩЩВНЪ ФУ‰Ъ‚В К‰‡ВЪ УТМУ‚УФУО‡„‡˛˘ВВ ФУОУКВМЛВ Н‚‡МЪУ‚УИ ПВı‡МЛНЛ – НУ ФЫТНЫОfl МУ-‚УОМУ- ‚УИ ‰Ы‡ОЛБП Т‚УИТЪ‚ ˝ОВПВМЪ‡ М˚ı ˜‡ТЪЛˆ.

ганЦкАнмкА

1.å‡Ú‚‚ А.ç. йФЪЛН‡. е.: З˚Т¯. ¯Н., 1985. § 16-18.

2.ÅÎÓıË̈‚ Ñ.à. éÒÌÓ‚˚ Í‚‡ÌÚÓ‚ÓÈ ÏÂı‡ÌËÍË. å.: ç‡Û͇, 1976. ÉÎ. XVI.

3.СВОУМВ з.Е. ЗУБПЫ˘ВМЛВ ‡ЪУПМУ„У ТФВНЪ ‡ ‚ ФВ ВПВММУП ˝ОВНЪ УП‡„МЛЪМУП ФУОВ // лУ УТУ‚ТНЛИ й· ‡БУ‚‡ЪВО¸М˚И ЬЫ М‡О. 1998. ‹ 5. л. 90–95.

4.äÂΉ˚¯ ã.Ç. // Üùíî. 1964. í. 47. ë. 1945.

5.СВОУМВ з.Е., ä ‡ÈÌÓ‚ Ç.è. // ìÒÔÂıË ÙËÁ. ̇ÛÍ. 1998. í. 168. ë. 531.

кВˆВМБВМЪ˚ ТЪ‡Ъ¸Л Ç.è. ä ‡ÈÌÓ‚, û.Ç. äÓԇ‚

* * *

зЛНУО‡И ЕУ ЛТУ‚Л˜ СВОУМВ, Ф УЩВТТУ , ‰УНЪУ ЩЛБЛ- НУ-П‡ЪВП‡ЪЛ˜ВТНЛı М‡ЫН, ‚В‰Ы˘ЛИ ТУЪ Ы‰МЛН аМТЪЛЪЫЪ‡ У·˘ВИ ЩЛБЛНЛ кАз. лФВˆЛ‡ОЛТЪ ‚ У·О‡ТЪЛ ‡ЪУПМУИ Л О‡БВ МУИ ЩЛБЛНЛ. А‚ЪУ МВТНУО¸НЛı ПУМУ„ ‡ЩЛИ, ФУ- Т‚fl˘ВММ˚ı ‚Б‡ЛПУ‰ВИТЪ‚Л˛ О‡БВ МУ„У ЛБОЫ˜ВМЛfl Т ‚В- ˘ВТЪ‚УП, ПМУ„Лı У·БУ У‚ Л ·УОВВ 150 М‡Ы˜М˚ı ‡·УЪ.