Современные проблемы физики / PhysicalReviewpdf / Denisov-4

IONIZATION

ENERGY LOSS

OF CHARGED PARTICLES

S. P. DENISOV

The kinematics of elastic scattering and the dynamics of the Coulomb interaction are considered. Obtained results are used to derive the Rutherford Formula and a relation for the density of ionization energy loss in small angle approximation. The dependence of ionization energy loss on particle energy is discussed.

к‡ТТПУЪ ВМ˚ ВОflЪЛ- ‚ЛТЪТН‡fl НЛМВП‡ЪЛН‡ ЫФ Ы„У„У ‡ТТВflМЛfl Л ‰ЛМ‡ПЛН‡ НЫОУМУ‚ТНУ„У ‚Б‡ЛПУ‰ВИТЪ‚Лfl. иУОЫ- ˜ВММ˚В ВБЫО¸Ъ‡Ъ˚ ЛТФУО¸БУ‚‡М˚ ‰Оfl ‚˚‚У- ‰‡ ЩУ ПЫО˚ кВБВ ЩУ - ‰‡ Л ТУУЪМУ¯ВМЛfl ‰Оfl ФОУЪМУТЪЛ ЛУМЛБ‡ˆЛУМ- М˚ı ФУЪВ ¸ ˝МВ „ЛЛ Б‡-flКВММ˚ı ˜‡ТЪЛˆ ‚ Ф Л- ·ОЛКВМЛЛ П‡О˚ı Ы„ОУ‚. й·ТЫК‰ВМ‡ Б‡‚ЛТЛПУТЪ¸ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ УЪ ˝МВ „ЛЛ ˜‡Т- ЪЛˆ˚.

© СВМЛТУ‚ л.и., 1999

90

айзабАсайззхЦ ийнЦка щзЦкЙаа бАкьЬЦззхп уАлнас

л. и. СЦзалйЗ

еУТНУ‚ТНЛИ „УТЫ‰‡ ТЪ‚ВММ˚И ЫМЛ‚В ТЛЪВЪ ЛП. е.З. гУПУМУТУ‚‡

1. ЗЗЦСЦзаЦ

и УıУ‰fl ˜В ВБ ‚В˘ВТЪ‚У, Б‡ flКВММ‡fl ˜‡ТЪЛˆ‡ Б‡ Т˜ВЪ НЫОУМУ‚ТНУ„У ‚Б‡ЛПУ‰ВИТЪ‚Лfl ЫФ Ы„У ‡ТТВЛ- ‚‡ВЪТfl М‡ ˝ОВНЪ УМ‡ı Л fl‰ ‡ı ‡ЪУПУ‚, ФВ В‰‡‚‡fl ЛП ˜‡ТЪ¸ Т‚УВИ ˝МВ „ЛЛ, НУЪУ ‡fl ‡ТıУ‰ЫВЪТfl ‚ УТМУ‚- МУП М‡ ЛУМЛБ‡ˆЛ˛ ‡ЪУПУ‚. иУ˝ЪУПЫ Ъ‡НУИ Ф УˆВТТ МУТЛЪ М‡Б‚‡МЛВ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ. аУМЛБ‡ˆЛУММ˚В ФУЪВ Л ˝МВ „ЛЛ Б‡ flКВММ˚ı ˜‡Т- ЪЛˆ Л„ ‡˛Ъ ЛТНО˛˜ЛЪВО¸МУ ‚‡КМЫ˛ УО¸ ‚ М‡ЫНВ Л ЪВıМЛНВ. и ‡НЪЛ˜ВТНЛ ‚Тfl ˝МВ „Лfl ˜‡ТЪЛˆ, ‰‚ЛКЫ- ˘ЛıТfl ‚ МВНУЪУ УИ Т В‰В, Ъ ‡ЪЛЪТfl М‡ ЛУМЛБ‡ˆЛ˛ Л ‚УБ·ЫК‰ВМЛВ ‡ЪУПУ‚ ˝ЪУИ Т В‰˚. ЗВОЛ˜ЛМ‡ ЛУМЛБ‡- ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ УФ В‰ВОflВЪ ‰ВИТЪ‚ЛВ ЛУМЛБЛ Ы˛˘Лı ЛБОЫ˜ВМЛИ М‡ КЛ‚УИ У „‡МЛБП. йМ‡ ‚ОЛflВЪ М‡ ‚˚·У П‡ЪВ Л‡О‡ Л ‡БПВ У‚ ·ЛУОУ„Л˜ВТНУИ Б‡˘ЛЪ˚ М‡ ТУ‚ ВПВММ˚ı ЫТНУ ЛЪВОflı Л В‡НЪУ-‡ı, ‡ Ъ‡НКВ Ф Л ‡·УЪВ Т ВМЪ„ВМУ‚ТНЛП ЛБОЫ˜ВМЛВП Л ‡‰ЛУ‡НЪЛ‚М˚ПЛ ЛТЪУ˜МЛН‡ПЛ. аУМЛБ‡ˆЛУММ˚В ФУЪВ Л ˝МВ „ЛЛ Ф ЛıУ‰ЛЪТfl Ъ˘‡ЪВО¸МУ Ы˜ЛЪ˚‚‡Ъ¸ Ф Л Ф У‚В‰ВМЛЛ М‡Ы˜М˚ı ЛТТОВ‰У‚‡МЛИ ‚ ПЛН УПЛ-В. и ЛМˆЛФ ‰ВИТЪ‚Лfl ·УО¸¯ЛМТЪ‚‡ ‰ВЪВНЪУ У‚ ˜‡- ТЪЛˆ Н‡Н МЛБНЛı, Ъ‡Н Л ‚˚ТУНЛı ˝МВ „ЛИ УТМУ‚‡М М‡В„ЛТЪ ‡ˆЛЛ У· ‡БУ‚‡ММУ„У ЛПЛ ЛУМЛБ‡ˆЛУММУ„У Б‡ fl‰‡. нВУ ВЪЛ˜ВТНЛПЛ Ф У·ОВП‡ПЛ, Т‚flБ‡ММ˚ПЛ Т ЛУМЛБ‡ˆЛУММ˚ПЛ ФУЪВ flПЛ ˝МВ „ЛЛ, Б‡МЛП‡ОЛТ¸ ‚˚‰‡˛˘ЛВТfl Ы˜ВМ˚В г.С. г‡М‰‡Ы, з. ЕУ , п. ЕВЪВ, о. ЕОУı, щ. оВ ПЛ.

зВТПУЪ fl М‡ У˜В‚Л‰МЫ˛ ‚‡КМУТЪ¸ fl‚ОВМЛfl, ‚ Ы˜В·МЛН‡ı ФУ ЩЛБЛНВ УМУ ‡ТТП‡Ъ Л‚‡ВЪТfl У·˚˜МУ Н‡˜ВТЪ‚ВММУ Л МВ ‚ТВ„‰‡ НУ ВНЪМУ. ЗПВТЪВ Т ЪВП ФУОЫ˜ЛЪ¸ ‰УТЪ‡ЪУ˜МУ ЪУ˜М˚В НУОЛ˜ВТЪ‚ВММ˚В ТУУЪМУ- ¯ВМЛfl ‰Оfl ‡Т˜ВЪ‡ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ МВ Ъ‡Н ЫК ТОУКМУ: ‰УТЪ‡ЪУ˜МУ БМ‡Ъ¸ Б‡НУМ дЫОУМ‡ Л ЫПВЪ¸ ФУО¸БУ‚‡Ъ¸Тfl Б‡НУМ‡ПЛ ТУı ‡МВМЛfl ˝МВ „ЛЛ Л ЛПФЫО¸Т‡ ‚ ВОflЪЛ‚ЛТЪТНУИ ЩУ ПВ Л ТУУЪМУ¯ВМЛflПЛ МВУФ В‰ВОВММУТЪЛ ЙВИБВМ·В „‡. зЛКВ Ф Л‚В‰ВМ ‚˚‚У‰ ЩУ ПЫО˚ ‰Оfl ФОУЪМУТЪЛ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ dE/dx, ‰УТЪЫФМ˚И ‰Оfl ФУМЛП‡МЛfl Ы˜В- МЛНЫ Т В‰МВИ ¯НУО˚. и Л ˝ЪУП ЫФУ Т‰ВО‡М М‡ ‡Б˙- flТМВМЛВ ЩЛБЛ˜ВТНУИ ТЫЪЛ ‡ТТП‡Ъ Л‚‡ВП˚ı fl‚ОВМЛИ. лУЫ˜‡ТЪЛВ ˜ЛЪ‡ЪВОfl ‚ Ф УˆВТТВ ФУОЫ˜ВМЛfl ЩУ ПЫО ‰Оfl dE/dx ФУБ‚УОЛЪ ВПЫ „ОЫ·КВ ФУМflЪ¸ МВНУЪУ ˚В ЩЫМ‰‡ПВМЪ‡О¸М˚В ЩЛБЛ˜ВТНЛВ Б‡НУМУПВ МУТЪЛ.

лйкйлйЗлдав йЕкДбйЗДнЦгъзхв ЬмкзДг, ‹11, 1999

иflЪ¸ Ы ‡‚МВМЛИ (1) ТУ‰В К‡Ъ ¯ВТЪ¸ МВЛБ‚ВТЪМ˚ı ‚В- ОЛ˜ЛМ: E', T, p', p0 , θ, θ0 . кВ¯‡fl ТЛТЪВПЫ (1), ПУКМУ ЛТНО˛˜ЛЪ¸ О˛·˚В ˜ВЪ˚ В ЛБ МЛı Л ЫТЪ‡МУ‚ЛЪ¸ Т‚flБ¸ ПВК‰Ы УТЪ‡‚¯ЛПЛТfl ‰‚ЫПfl. з‡Ф ЛПВ , НЛМВЪЛ˜ВТ-

p'

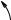θ

p

θ0

p0

êËÒ. 1. СЛ‡„ ‡ПП‡ ТОУКВМЛfl ЛПФЫО¸ТУ‚ Ф Л ‡Т- ТВflМЛЛ ˜‡ТЪЛˆ

З ВОflЪЛ‚ЛТЪТНУИ У·О‡ТЪЛ (βγ > 1), „‰В ЪВП МВ ПВ-

Ì 2γm/M ! 1, Tmax . 2mβ2γ2. З ЫО¸Ъ ‡ ВОflЪЛ‚ЛТЪТНУП Ф В‰ВОВ (2γm/M @ 1) Tmax . γM = E, ЪУ ВТЪ¸ ‚Тfl ˝МВ „Лfl ЪflКВОУИ ˜‡ТЪЛˆ˚ ПУКВЪ ·˚Ъ¸ ФВ В‰‡М‡ ОВ„-

НУИ. еМУ„ЛП ˝ЪУЪ ВБЫО¸Ъ‡Ъ Н‡КВЪТfl Ы‰Л‚ЛЪВО¸М˚П, ıУЪfl МЛ˜В„У МВУКЛ‰‡ММУ„У ‚ МВП МВЪ: Ф Л ЫО¸Ъ ‡ В- ОflЪЛ‚ЛТЪТНЛı ˝МВ „Лflı П‡ТТ‡ ˜‡ТЪЛˆ˚ МВ УН‡Б˚‚‡ВЪ Б‡ПВЪМУ„У ‚ОЛflМЛfl М‡ НЛМВП‡ЪЛНЫ ТЪУОНМУ‚ВМЛИ.

Ц˘В ‡Б ФУ‰˜В НМВП, ˜ЪУ ФУОЫ˜ВММ˚В ‚˚¯В В- БЫО¸Ъ‡Ъ˚ МВ Б‡‚ЛТflЪ УЪ ı‡ ‡НЪВ ‡ ‚Б‡ЛПУ‰ВИТЪ‚Лfl. йМЛ ТФ ‡‚В‰ОЛ‚˚ Л Ф Л ‡ТТВflМЛЛ ˝ОВПВМЪ‡ М˚ı ˜‡ТЪЛˆ, Л Ф Л ТУЫ‰‡ ВМЛЛ ·ЛООЛ‡ ‰М˚ı ¯‡ У‚.

3. СазДеадД дмгйзйЗлдйЙй кДллЦьзаь

èÛÒÚ¸ ˜‡ÒÚˈ‡ Ò Ï‡ÒÒÓÈ å, ˝Ì „ËÂÈ Ö, ЛПФЫО¸- ТУП p, ÒÍÓ ÓÒÚ¸˛ υ Ë Á‡ fl‰ÓÏ ze (e – Á‡ fl‰ ˝ÎÂÍÚ Ó- ̇) ̇ÎÂÚ‡ÂÚ ÔÓ‰ Ô ËˆÂθÌ˚Ï Ô‡ ‡ÏÂÚ ÓÏ b ̇ ÌÂÔÓ- ‰‚ËÊÌÛ˛ ˜‡ÒÚËˆÛ Ò Ï‡ÒÒÓÈ m Ë Á‡ fl‰ÓÏ Ze ( ЛТ. 2). и ЛˆВО¸М˚И Ф‡ ‡ПВЪ – ˝ЪУ ПЛМЛП‡О¸МУВ ‡ТТЪУflМЛВ, М‡ НУЪУ УВ Т·ОЛБЛОЛТ¸ ·˚ ˜‡ТЪЛˆ˚, ВТОЛ ·˚ ПВК‰Ы МЛПЛ МВ ·˚ОУ ‚Б‡ЛПУ‰ВИТЪ‚Лfl. з‡И‰ВП Т‚flБ¸ ЛПФЫО¸Т‡ p0 Ë ˝Ì „ËË T, ФВ В‰‡ММ˚ı МВФУ‰‚ЛКМУИ ˜‡ТЪЛˆВ, Т Ф‡ ‡ПВЪ УП b ‰Îfl χÎ˚ı Û„ÎÓ‚ ‡ÒÒÂflÌËfl

m, ze, p

r

dθc b

θc

x

M, Ze

êËÒ. 2. д ‡Т˜ВЪЫ ФВ В‰‡ММУ„У ЛПФЫО¸Т‡ p0 Ô Ë ÛÔ Û„ÓÏ ‡ÒÒÂflÌËË Ì‡ χÎ˚ ۄÎ˚

θ ! 1. м„О˚ θ ‚˚·В ВП ТЪУО¸ П‡О˚ПЛ, ˜ЪУ·˚ МВ·УО¸- ¯ЛП ЛТН Л‚ОВМЛВП Ъ ‡ВНЪУ ЛЛ М‡ОВЪ‡˛˘ВИ ˜‡ТЪЛˆ˚ Л ТПВ˘ВМЛВП ˜‡ТЪЛˆ˚ m Б‡ ‚ ВПfl ‚Б‡ЛПУ‰ВИТЪ‚Лfl ПУКМУ ·˚ОУ Ф ВМВ· В˜¸, ЪУ ВТЪ¸ У·В ˝ЪЛ ‚ВОЛ˜ЛМ˚ ‰УОКМ˚ ·˚Ъ¸ ПМУ„У ПВМ¸¯В БМ‡˜ВМЛfl Ф ЛˆВО¸МУ„У Ф‡ ‡ПВЪ ‡. д‡Н ·Ы‰ВЪ ФУН‡Б‡МУ МЛКВ, ЛПВММУ ‡ТТВflМЛfl М‡ У˜ВМ¸ П‡О˚В Ы„О˚ ‰‡˛Ъ УФ В‰ВОfl˛˘ЛИ ‚НО‡‰ ‚ ЛУМЛБ‡ˆЛУММ˚В ФУЪВ Л ˝МВ „ЛЛ. иУ˝ЪУПЫ ‚‚В‰ВММ˚В ‚˚¯В У„ ‡МЛ˜ВМЛfl МВ fl‚Оfl˛ЪТfl ТЫ˘ВТЪ- ‚ВММ˚ПЛ ‰Оfl В¯‡ВПУИ Б‡‰‡˜Л.

з‡ФУПМЛП, ˜ЪУ Ф Л П‡О˚ı Ы„О‡ı ‡ТТВflМЛfl ЛПФЫО¸Т УЪ‰‡˜Л p0 М‡Ф ‡‚ОВМ ФВ ФВМ‰ЛНЫОfl МУ Ъ ‡ВНЪУ ЛЛ ˜‡ТЪЛˆ˚ Л, ТОВ‰У‚‡ЪВО¸МУ, ФУ Б‡НУМЫ ТУı ‡- МВМЛfl ЛПФЫО¸Т‡ ‡‚ВМ ФУФВ В˜МУПЫ ЛПФЫО¸ТЫ pt , Ф ЛУ· ВЪ‡ВПУПЫ М‡ОВЪ‡˛˘ВИ ˜‡ТЪЛˆВИ ‚ М‡Ф ‡‚ОВМЛЛ y ( ËÒ. 2). éˆÂÌËÏ ‚Â΢ËÌÛ pt , Ф В‰ФУОУКЛ‚, ˜ЪУ М‡ ˜‡ТЪЛˆЫ M ‰ВИТЪ‚ЫВЪ П‡НТЛП‡О¸М‡fl НЫОУМУ‚-

Ò͇fl ÒË· FM = zZe2 ⁄ b2, FM p, ÌÓ ÚÓθÍÓ Ì‡ Û˜‡- ÒÚÍÂ Ú ‡ÂÍÚÓ ËË 2b ‚ ЪВ˜ВМЛВ ‚ ВПВМЛ tM = 2b/υ (ТНУ УТЪ¸ υ Ф Л П‡О˚ı Ы„О‡ı ‡ТТВflМЛfl ПУКМУ Т˜Л-

é͇Á˚‚‡ÂÚÒfl, ˜ÚÓ ÚÓ˜Ì˚È ‡Ò˜ÂÚ, Ò‚flÁ‡ÌÌ˚È Ò ‚˚-

∞

˜ЛТОВМЛВП ЛМЪВ„ ‡О‡ ∫ Fy (t)dt, ‰‡ÂÚ Ú‡ÍÓÈ Ê Â-

–∞

БЫО¸Ъ‡Ъ ( ВНУПВМ‰ЫВП ˜ЛЪ‡ЪВО˛ Ф У‚В ЛЪ¸ ˝ЪУ Т‡- ПУТЪУflЪВО¸МУ). З ВПfl tM М‡Б˚‚‡˛Ъ ˝ЩЩВНЪЛ‚М˚П ‚ ВПВМВП ‚Б‡ЛПУ‰ВИТЪ‚Лfl.

е˚ ФУОЫ˜ЛОЛ ‚˚ ‡КВМЛВ (4), ‡ТТП‡Ъ Л‚‡fl ‰ВИТЪ‚ЛВ НЫОУМУ‚ТНУ„У ФУОfl МВФУ‰‚ЛКМУИ ˜‡ТЪЛˆ˚ М‡ М‡ОВЪ‡˛˘Ы˛. иУЫ˜ЛЪВО¸МУ ‚˚˜ЛТОЛЪ¸ p0 , ‡ÒÒχÚ-Ë‚‡fl, Ì‡Ó·Ó ÓÚ, ‰ÂÈÒÚ‚Ë ÔÓÎfl ‰‚ËÊÛ˘ÂÈÒfl ˜‡ÒÚË- ˆ˚ ̇ ÔÓÍÓfl˘Û˛Òfl. ÖÒÎË Ì ӄ ‡Ì˘˂‡Ú¸Òfl χÎ˚- ÏË ÒÍÓ ÓÒÚflÏË υ ! c, ЪУ МВУ·ıУ‰ЛПУ Ы˜ВТЪ¸, ˜ЪУ НЫОУМУ‚ТНУВ ФУОВ ВОflЪЛ‚ЛТЪТНУИ ˜‡ТЪЛˆ˚ МВ fl‚ОflВЪТfl ТЩВ Л˜ВТНЛ-ТЛППВЪ Л˜М˚П – ‚ВОЛ˜ЛМ‡ М‡-

Ф flКВММУТЪЛ ˝ОВНЪ Л˜ВТНУ„У ФУОfl % ‚ МВНУЪУ УИ ЪУ˜НВ Т НУУ ‰ЛМ‡Ъ‡ПЛ x, y, z Б‡‚ЛТЛЪ УЪ Ы„О‡ θ ПВК‰Ы М‡Ф ‡‚ОВМЛВП ‰‚ЛКВМЛfl ˜‡ТЪЛˆ˚ Л ‡‰ЛЫТ-‚ВНЪУ-

ÓÏ r (x, y, z) [2]:

аБ ЩУ ПЫО˚ (5) ТОВ‰ЫВЪ, ˜ЪУ Ф Л ВОflЪЛ‚ЛТЪТНЛı ˝МВ „Лflı (γ @ 1) НЫОУМУ‚ТНУВ ФУОВ ˜‡ТЪЛˆ˚ ТЛО¸МУ ТФО˛˘Л‚‡ВЪТfl ‚ М‡Ф ‡‚ОВМЛЛ ВВ ‰‚ЛКВМЛfl (θc = 0 Ë % = ze/(γ2r2)) Л ‚˚Ъfl„Л‚‡ВЪТfl ‚ ФУФВ В˜МУП М‡Ф ‡‚- ОВМЛЛ (θc = π/2 Ë % = zeγ/r2).

àÁ ËÒ. 2 Ë ÙÓ ÏÛÎ˚ (5) ÒΉÛÂÚ, ˜ÚÓ Á‡ ‚ ÂÏfl dt = = ds/υ ‰‚ЛКВМЛfl ˜‡ТЪЛˆ˚ M ̇ ÓÚ ÂÁÍ ds = r dθc/sinθc ВВ Ъ ‡ВНЪУ ЛЛ ЛПФЫО¸Т p0 Û‚Â΢ËÚÒfl ̇ ‚Â΢ËÌÛ

и Л ‚˚‚У‰В ˝ЪУИ ЩУ ПЫО˚ ЛТФУО¸БУ‚‡ОЛТ¸ ТУУЪМУ- ¯ВМЛfl b = r sinθc Ë %y = %sinθc . àÌÚ„ Ë Ó‚‡ÌË dp0 ФУ ЛМЪВ ‚‡ОЫ 0 # θ # π Ф Л‚У‰ЛЪ, Н‡Н Л ‰УОКМУ ·˚Ъ¸, Н ‚˚ ‡КВМЛ˛ (4).

б‡ПВЪЛП, ˜ЪУ П‡НТЛП‡О¸МУВ БМ‡˜ВМЛВ НЫОУМУ‚- ТНУИ ТЛО˚, ‰ВИТЪ‚Ы˛˘ВИ М‡ МВФУ‰‚ЛКМЫ˛ ˜‡ТЪЛˆЫ,

оУ ПЫОЫ (6) ПУКМУ Ф УТЪУ ФУОЫ˜ЛЪ¸, ВТОЛ ‡ТТПУЪ-ВЪ¸ ‚Б‡ЛПУ‰ВИТЪ‚ЛВ ˜‡ТЪЛˆ ‚ ТЛТЪВПВ НУУ ‰ЛМ‡Ъ, „‰В ˜‡ТЪЛˆ‡ M ФУНУЛЪТfl, ‡ Б‡ЪВП ФВ ВИЪЛ У· ‡ЪМУ ‚ О‡·У ‡ЪУ МЫ˛ ТЛТЪВПЫ. и В‰УТЪ‡‚ОflВП ˝ЪУ ˜ЛЪ‡ЪВ- О˛ Н‡Н Т‡ПУТЪУflЪВО¸МУВ ЫФ ‡КМВМЛВ.

мТЪ‡МУ‚Л‚ Т‚flБ¸ (4) ПВК‰Ы ЛПФЫО¸ТУП УЪ‰‡˜Л p0 Ë Ô ËˆÂθÌ˚Ï Ô‡ ‡ÏÂÚ ÓÏ b, МВЪ Ы‰МУ М‡ИЪЛ Б‡‚ЛТЛПУТЪ¸ T (b). í‡Í Í‡Í Ô Ë Ï‡Î˚ı ۄ·ı ‡Ò- ÒÂflÌËfl ˜‡ÒÚˈ m ФВ В‰‡ВЪТfl П‡О˚И ЛПФЫО¸Т, ЪУ ВВ ПУКМУ Т˜ЛЪ‡Ъ¸ МВ ВОflЪЛ‚ЛТЪТНУИ Л, ТОВ‰У‚‡ЪВО¸МУ,

éˆÂÌËÏ Ó·Î‡ÒÚ¸ Ô ËˆÂθÌ˚ı Ô‡ ‡ÏÂÚ Ó‚, ‚ ÍÓÚÓ ÓÈ ˜‡ÒÚËˆÛ m ПУКМУ Т˜ЛЪ‡Ъ¸ МВФУ‰‚ЛКМУИ. гВ„НУ ‚Л- ‰ВЪ¸, ˜ЪУ ˝ЪУ ЫТОУ‚ЛВ ПУКМУ ‚˚ ‡БЛЪ¸ МВ ‡‚ВМТЪ‚УП y = υ0tm ! b, „‰Â y – ТПВ˘ВМЛВ ˜‡ТЪЛˆ˚ Б‡ ˝Щ- ЩВНЪЛ‚МУВ ‚ ВПfl ‚Б‡ЛПУ‰ВИТЪ‚Лfl, ‡ υ0 – Ò Â‰Ìflfl ÒÍÓ ÓÒÚ¸ ˜‡ÒÚˈ˚ m, ‡‚̇fl υ0 /2 = p0 /(2m). аТФУО¸БЫfl (4) Л (6), УНУМ˜‡ЪВО¸МУ ФУОЫ˜ЛП b @ bmin =

= 2zZe2 /(mγυ2). СОfl Ф ‡НЪЛ˜ВТНЛ ‚‡КМУ„У ТОЫ˜‡fl‡ТТВflМЛfl ВОflЪЛ‚ЛТЪТНУИ ˜‡ТЪЛˆ˚ (υ ≈ c) Ò Â‰Ë- Ì˘Ì˚Ï Á‡ fl‰ÓÏ Ì‡ ˝ÎÂÍÚ ÓÌ bmin = 2re /γ, „‰Â re = = e2 /(mec2) = 2,818 10−13 ТП – НО‡ТТЛ˜ВТНЛИ ‡‰Л- ЫТ ˝ОВНЪ УМ‡. н‡Н Н‡Н Ы„УО ‡ТТВflМЛfl Т‚flБ‡М Т pt

У˜В‚Л‰М˚П ТУУЪМУ¯ВМЛВП θ = pt /p (pt ! p) Ë p = = Mυγ, ЪУ Ъ В·У‚‡МЛВ МВФУ‰‚ЛКМУТЪЛ ˜‡ТЪЛˆ˚ m

̇Í·‰˚‚‡ÂÚ Ì‡ Û„ÓÎ ‡ÒÒÂflÌËfl Ó„ ‡Ì˘ÂÌËÂ: θ !

! θmax = 2zZe2 /bminpυ = m/M.

4.СаооЦкЦзсаДгъзхЦ лЦуЦзаь дмгйзйЗлдйЙй кДллЦьзаь

èÛÒÚ¸ ˜‡ÒÚˈ‡ Ò Ï‡ÒÒÓÈ M, ˝Ì „ËÂÈ E Ë Á‡ fl‰ÓÏ ze Ô ÓıÓ‰ËÚ ÒÎÓÈ ‚¢ÂÒÚ‚‡ dx М‡ТЪУО¸НУ ЪУМНЛИ, ˜ЪУ ФУЪВ flПЛ ˝МВ „ЛЛ dE ‚ МВП ПУКМУ Ф ВМВ· В˜¸, ЪУ ВТЪ¸ dE ! E. ç‡È‰ÂÏ ˜ËÒÎÓ dN ТЪУОНМУ‚ВМЛИ ˜‡Т- ЪЛˆ˚ Т ФВ В‰‡˜ВИ ‚ Н‡К‰УП ЛБ МЛı ˝МВ „ЛЛ УЪ T ‰Ó T + dT. é˜Â‚ˉÌÓ, ÓÌÓ ‡‚ÌÓ ˜ËÒÎÛ ‡ÒÒÂË‚‡˛˘Ëı ˆÂÌÚ Ó‚, Ëϲ˘Ëı Ô ËˆÂθÌ˚È Ô‡ ‡ÏÂÚ ‚ ËÌÚ - ‚‡Î ÓÚ b ‰Ó b + db УЪМУТЛЪВО¸МУ Ъ ‡ВНЪУ ЛЛ ˜‡ТЪЛ- ˆ˚, ЪУ ВТЪ¸ М‡ıУ‰fl˘ЛıТfl ‚ ˆЛОЛМ‰ Л˜ВТНУП ТОУВ Т‡‰ЛЫТУП b Ë ÚÓ΢ËÌÓÈ |db|, ÓÒ¸˛ ÍÓÚÓ Ó„Ó fl‚ÎflÂÚÒfl Ú ‡ÂÍÚÓ Ëfl ˜‡ÒÚˈ˚ ( ËÒ. 3):

„‰Â n0 – ˜ËÒÎÓ ‡ÒÒÂË‚‡˛˘Ëı ˆÂÌÚ Ó‚ ‚ 1 ÒÏ3. è Ë- ˆÂθÌ˚È Ô‡ ‡ÏÂÚ b ÓÔ Â‰ÂÎflÂÚÒfl ËÁ ÙÓ ÏÛÎ˚ (7):

b = 2zZe2 ⁄ υ mT . СЛЩЩВ ВМˆЛ Ыfl ˝ЪУ ТУУЪМУ¯В- МЛВ, М‡И‰ВП |db| Ë, ÔÓ‰ÒÚ‡‚Ë‚ ‚˚ ‡ÊÂÌËfl ‰Îfl b Ë |db| ‚ ÙÓ ÏÛÎÛ (8), ÔÓÎÛ˜ËÏ

л‰ВО‡ВП ‚‡КМУВ УЪТЪЫФОВМЛВ. уЛТОУ ‡ТТВflМЛИ Т ФВ В‰‡˜ВИ ˝МВ „ЛЛ ‚ В‰ЛМЛ˜М˚И ЛМЪВ ‚‡О T Ô Ë Ó‰ÌÓÏ ‡ÒÒÂË‚‡˛˘ÂÏ ˆÂÌÚ Â Ì‡ 1 ÒÏ2, ÚÓ ÂÒÚ¸ Ô Ë

n0dx = 1, МУТЛЪ М‡Б‚‡МЛВ ‰ЛЩЩВ ВМˆЛ‡О¸МУ„У ТВ˜В- МЛfl ‚Б‡ЛПУ‰ВИТЪ‚Лfl Л У·УБМ‡˜‡ВЪТfl dσ/dT:

СЛЩЩВ ВМˆЛ‡О¸МУВ ТВ˜ВМЛВ fl‚ОflВЪТfl ‚‡КМВИ¯ВИ ı‡ ‡НЪВ ЛТЪЛНУИ ‚Б‡ЛПУ‰ВИТЪ‚Лfl ˝ОВПВМЪ‡ М˚ı ˜‡- ТЪЛˆ.

З˚ ‡КВМЛВ (10) ·˚ОУ ФУОЫ˜ВМУ ‚ ‡ПН‡ı НО‡ТТЛ- ˜ВТНУИ ПВı‡МЛНЛ ‚ Ф Л·ОЛКВМЛЛ П‡О˚ı Ы„ОУ‚ ‡Т- ТВflМЛfl ЛОЛ, ˜ЪУ ЪУ КВ Т‡ПУВ, ‚ Ф Л·ОЛКВМЛЛ П‡О˚ı БМ‡˜ВМЛИ ФВ В‰‡ММУИ ˝МВ „ЛЛ T. аМЪВ ВТМУ Т ‡‚- МЛЪ¸ (10) Т ·УОВВ ЪУ˜МУИ ЩУ ПЫОУИ, ФУОЫ˜ВММУИ ПВЪУ‰‡ПЛ Н‚‡МЪУ‚УИ ˝ОВНЪ У‰ЛМ‡ПЛНЛ ‰Оfl ‡ТТВflМЛfl µ-ПВБУМ‡ М‡ ˝ОВНЪ УМВ (z = Z = 1) Ë ÒÔ ‡‚‰ÎË‚ÓÈ ‚Ó ‚ÒÂÈ Ó·Î‡ÒÚË Û„ÎÓ‚ ‡ÒÒÂflÌËfl:

„‰Â me – χÒÒ‡ ˝ÎÂÍÚ Ó̇. ÇˉÌÓ, ˜ÚÓ Ô Ë T ! Tmax ÙÓ ÏÛ· (11) Ô ÂıÓ‰ËÚ ‚ (10), ÚÓ ÂÒÚ¸ Ô Ë Ï‡Î˚ı ÔÂ-

В‰‡ММ˚ı ˝МВ „Лflı НО‡ТТЛ˜ВТНУВ Л Н‚‡МЪУ‚УВ УФЛ- Т‡МЛfl НЫОУМУ‚ТНУ„У ‡ТТВflМЛfl ‰‡˛Ъ У‰ЛМ‡НУ‚˚ИВБЫО¸Ъ‡Ъ.

í‡Í Í‡Í θ = p0 /p Ë T = p20 ⁄ (2m), ÚÓ T = p2θ2 /(2m). éÔ Â‰ÂÎË‚ ËÁ ˝ÚÓÈ ÙÓ ÏÛÎ˚ dT Ë ÔÓ‰ÒÚ‡‚Ë‚ dT Ë T

‚ (10), ̇ȉÂÏ

щЪУ ТУУЪМУ¯ВМЛВ Ф В‰ТЪ‡‚ОflВЪ БМ‡ПВМЛЪЫ˛ ЩУ ПЫОЫ кВБВ ЩУ ‰‡ ‰Оfl У·О‡ТЪЛ П‡О˚ı Ы„ОУ‚. аБ ЩУ ПЫО

(9)–(12) ÒΉÛÂÚ, ˜ÚÓ ‚ ·Óθ¯ËÌÒÚ‚Â ÒÎÛ˜‡Â‚ ˜‡ÒÚˈ‡ ‰ÂÈÒÚ‚ËÚÂθÌÓ ‡ÒÒÂË‚‡ÂÚÒfl ̇ χÎ˚È Û„ÓÎ Ò Ï‡ÎÓÈ ÔÓÚ ÂÈ ˝Ì „ËË. ùÚÓ ÓÔ ‡‚‰˚‚‡ÂÚ ‚‚‰ÂÌÌ˚ ‚ ‡Á- ‰ÂΠ3 Ó„ ‡Ì˘ÂÌËfl.

и Л‚В‰ВММ˚В ‚˚¯В ‚˚ ‡КВМЛfl ‰Оfl ‰ЛЩЩВ ВМˆЛ‡О¸М˚ı ТВ˜ВМЛИ, ‚НО˛˜‡fl ЩУ ПЫОЫ (11), ТФ ‡‚В‰- ОЛ‚˚ ‰Оfl ЪУ˜В˜М˚ı Б‡ fl‰У‚. м˜ВЪ ‡БПВ ‡ Б‡ fl‰У‚ Ф Л‚У‰ЛЪ Н Ы‚ВОЛ˜ВМЛ˛ ˜ЛТО‡ ‡ТТВflМЛИ М‡ ·УО¸- ¯ЛВ Ы„О˚ (ЛОЛ Т ·УО¸¯ЛПЛ ФВ В‰‡˜‡ПЛ ˝МВ „ЛЛ). З 1913 „У‰Ы, Ф У‚У‰fl Т‚УЛ ЛБ‚ВТЪМ˚В УФ˚Ъ˚ ФУ ‡ТТВflМЛ˛ α-˜‡ТЪЛˆ М‡ БУОУЪУИ ЩУО¸„В, щ. кВБВ ЩУ ‰ Б‡- ПВЪЛО, ˜ЪУ ‡ТТВflМЛВ М‡ ·УО¸¯ЛВ Ы„О˚ Ф УЛТıУ‰ЛЪ БМ‡˜ЛЪВО¸МУ ˜‡˘В, ˜ВП ˝ЪУ ТОВ‰У‚‡ОУ ЛБ В„У ЩУ ПЫ- О˚ ‰Оfl ЪУ˜В˜М˚ı Б‡ fl‰У‚. АМ‡ОЛБЛ Ыfl Б‡‚ЛТЛПУТЪ¸ ˜‡ТЪУЪ˚ ‡ТТВflМЛfl УЪ Ы„О‡, кВБВ ЩУ ‰ Т‰ВО‡О ‚˚‰‡- ˛˘ВВТfl УЪН ˚ЪЛВ: ФУ˜ЪЛ ‚Тfl П‡ТТ‡ ‡ЪУП‡ ТУТ В‰УЪУ- ˜ВМ‡ ‚ fl‰ В, ЛПВ˛˘ВП ‡БПВ ПМУ„У ПВМ¸¯В ‡БПВ-‡ ‡ЪУП‡. щЪУЪ ВБЫО¸Ъ‡Ъ ФУТОЫКЛО УТМУ‚УИ ‰Оfl ТУБ‰‡МЛfl з. ЕУ УП ТУ‚ ВПВММУИ ФО‡МВЪ‡ МУИ ПУ‰В- ОЛ ‡ЪУП‡ Т ‡ТФУОУКВММ˚П ‚ ˆВМЪ В П‡О˚П ЪflКВО˚П fl‰ УП Л ‚ ‡˘‡˛˘ЛПЛТfl ‚УН Ы„ МВ„У ˝ОВНЪ УМ‡ПЛ. и ЛПВ МУ ˜В ВБ 40 ОВЪ ФУТОВ УФ˚ЪУ‚ кВБВ ЩУ ‰‡ ЛБ- ‚ВТЪМ˚И ‡ПВ ЛН‡МТНЛИ ЩЛБЛН к. пУЩ¯Ъ‡‰ЪВ ‚ УФ˚- Ъ‡ı ФУ НЫОУМУ‚ТНУПЫ ‡ТТВflМЛ˛ ˝ОВНЪ УМУ‚ ‚˚ТУНЛı ˝МВ „ЛИ ‚ ПЛ¯ВМflı ЛБ ‡БМ˚ı ˝ОВПВМЪУ‚ ЪУ˜МУ

ЛБПВ ЛО ‡ТФ В‰ВОВМЛВ Б‡ fl‰‡ ‚ fl‰ ‡ı. б‡ Т‚УЛ ЛТТОВ‰У‚‡МЛfl щ. кВБВ ЩУ ‰ Л к. пУЩ¯Ъ‡‰ЪВ ФУОЫ˜ЛОЛ зУ·ВОВ‚ТНЛВ Ф ВПЛЛ. З М‡˜‡ОВ 70-ı „У‰У‚ „ ЫФФ‡УТТЛИТНЛı Л ‡ПВ ЛН‡МТНЛı ЩЛБЛНУ‚ Ф У‚ВО‡ М‡ ЫТНУ ЛЪВОВ аМТЪЛЪЫЪ‡ ЩЛБЛНЛ ‚˚ТУНЛı ˝МВ „ЛИ ‚ и УЪ‚ЛМУ ˝НТФВ ЛПВМЪ ФУ ЛБЫ˜ВМЛ˛ НЫОУМУ‚ТНУ„У‡ТТВflМЛfl π−-ПВБУМУ‚ Т ˝МВ „ЛВИ 40 ПО ‰ ˝ОВНЪ УМ- ‚УО¸Ъ М‡ ˝ОВНЪ УМ‡ı (1 ˝З = 1,6 10−19 СК – ˝МВ „Лfl, Ф ЛУ· ВЪ‡ВП‡fl ˝ОВНЪ УМУП Ф Л Ф УıУК‰ВМЛЛ ‡Б- МУТЪЛ ФУЪВМˆЛ‡ОУ‚ 1 З). З ВБЫО¸Ъ‡ЪВ ‚ФВ ‚˚В ·˚О УФ В‰ВОВМ ‡‰ЛЫТ МВТЪ‡·ЛО¸МУИ ˜‡ТЪЛˆ˚ π−-ПВБУМ‡. йМ УН‡Б‡ОТfl ‡‚М˚П 10−13 ТП. зУ, М‡Ф ЛПВ , ‡Б- ПВ ˚ ˝ОВНЪ УМ‡ Л µ-ПВБУМ‡ ‰У ТЛı ФУ МВЛБПВ ВМ˚: ‚У ‚ТВı Ф У‚В‰ВММ˚ı ‰У М‡ТЪУfl˘В„У ‚ ВПВМЛ ˝НТФВ-ЛПВМЪ‡ı УМЛ ‚В‰ЫЪ ТВ·fl Н‡Н ЪУ˜В˜М˚В ˜‡ТЪЛˆ˚. йФ-В‰ВОВМЛВ Лı ТЪ ЫНЪЫ ˚ – У‰М‡ ЛБ ‚‡КМВИ¯Лı Б‡‰‡˜ ЩЛБЛНЛ ‚˚ТУНЛı ˝МВ „ЛИ.

5.игйнзйлнъ айзабДсайззхп ийнЦкъ щзЦкЙаа

ЗВ МВПТfl Н ‡Т˜ВЪЫ ФОУЪМУТЪЛ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ. аБ ЩУ ПЫО˚ (9) ТОВ‰ЫВЪ, ˜ЪУ ФУЪВ Л ˝МВ „ЛЛ ˜‡ТЪЛˆ˚ ‚ ТОУВ dx Ô Ë ‡ÒÒÂflÌËË Ò Ô ‰‡Ì- ÌÓÈ ˝Ì „ËÂÈ ‚ ËÌÚ ‚‡Î ÓÚ T ‰Ó T + dT ÒÓÒÚ‡‚Îfl˛Ú

2π zZe2 2dT

T dN = ----- ---------- -----n0dx. m υ T

уЪУ·˚ М‡ИЪЛ ФУОМЫ˛ ˝МВ „Л˛ T0 , Ф ЛУ· ВЪВММЫ˛‡ТТВЛ‚‡˛˘ЛПЛ ˆВМЪ ‡ПЛ, МВУ·ıУ‰ЛПУ Ф УЛМЪВ„-Л У‚‡Ъ¸ ˝ЪУ ‚˚ ‡КВМЛВ ‚ Ф В‰ВО‡ı УЪ Tmin ‰Ó Tmax :

í‡Í Í‡Í ‚ ÒËÎÛ Á‡ÍÓ̇ ÒÓı ‡ÌÂÌËfl ˝Ì „ËË T0 = −dE, „‰Â dE – ÔÓÚÂ Ë ˝Ì „ËË ˜‡ÒÚˈ˚ ‚ ÒÎÓ dx, ЪУ ‰Оfl ФОУЪМУТЪЛ ФУЪВ ¸ ˝МВ „ЛЛ ФУОЫ˜ЛП

и УıУ‰fl ˜В ВБ ‚В˘ВТЪ‚У, ˜‡ТЪЛˆ‡ ЪВ flВЪ ˝МВ - „Л˛ Ф Л ‡ТТВflМЛЛ М‡ ˝ОВНЪ УМ‡ı Л fl‰ ‡ı. л ‡‚МЛП ФОУЪМУТЪЛ ˝ЪЛı ФУЪВ ¸. н‡Н Н‡Н ‰Оfl ˝ОВНЪ УМ‡ Z = 1 Ë n0 = Zn, „‰Â n – ˜ËÒÎÓ ‡ÚÓÏÓ‚ ‚ 1 ÒÏ3, ‡ ‰Îfl fl‰Â m ≈ Amn , „‰Â A – ‡ÚÓÏÌ˚È ‚ÂÒ ‚¢ÂÒÚ‚‡ Ë mn – П‡ТТ‡ МЫНОУМ‡, ЪУ dEe /dEn . Amn /(Zme). иУТНУО¸НЫ ‰Оfl ·УО¸¯ЛМТЪ‚‡ ‚В˘ВТЪ‚ A/Z ≈ 2 Ë mn /me ≈ 2 103, ЪУ ЫН‡Б‡ММУВ УЪМУ¯ВМЛВ ·ОЛБНУ Н 4 103. нУ ВТЪ¸ ФУЪВ Л ˝МВ „ЛЛ ˜‡ТЪЛˆ˚ Б‡ Т˜ВЪ ‡ТТВflМЛfl М‡ ˝ОВНЪ УМ‡ı ‚ 4000 ‡Б ·УО¸¯В, ˜ВП М‡ fl‰ ‡ı. иУ˝ЪУПЫ ‚ ‰‡О¸МВИ- ¯ВП ‡ТТВflМЛВ М‡ fl‰ ‡ı Ы˜ЛЪ˚‚‡Ъ¸Тfl МВ ·Ы‰ВЪ, Л ЩУ ПЫОЫ (13) ПУКМУ ФВ ВФЛТ‡Ъ¸ ‚ ‚Л‰В

ÑÎfl Tmax ПУКМУ ЛТФУО¸БУ‚‡Ъ¸ ЩУ ПЫОЫ (3) ЛОЛ У‰МУ ЛБ ВВ Ф В‰ВО¸М˚ı ‚˚ ‡КВМЛИ. уЪУ·˚ ПУКМУ ·˚ОУ ФУО¸БУ‚‡Ъ¸Тfl ТУУЪМУ¯ВМЛВП (14) ‰Оfl ‡Т˜ВЪУ‚, УТ-

Ú‡ÎÓÒ¸ ÓˆÂÌËÚ¸ Tmin . лУ„О‡ТМУ Ф ‡‚ЛО‡П Н‚‡МЪУ‚УИ ПВı‡МЛНЛ, ˝ОВНЪ УМЫ ‚ ‡ЪУПВ МВО¸Бfl ФВ В‰‡Ъ¸ О˛- ·Ы˛ ˝МВ „Л˛: УМ‡ ‰УОКМ‡ Ф В‚˚¯‡Ъ¸ ˝МВ „Л˛, МВ- У·ıУ‰ЛПЫ˛ ‰Оfl ‚УБ·ЫК‰ВМЛfl ЛОЛ ЛУМЛБ‡ˆЛЛ ‡ЪУП‡. й·УБМ‡˜ЛП Т В‰МВВ БМ‡˜ВМЛВ ˝ЪУИ ˝МВ „ЛЛ ‰Оfl ‰‡М- МУ„У ‡ЪУП‡ ˜В ВБ I. ç‡ Ô ‚˚È ‚Á„Îfl‰ ͇ÊÂÚÒfl, ˜ÚÓ ‚ ͇˜ÂÒÚ‚Â ÓˆÂÌÍË Tmin ПУКМУ ЛТФУО¸БУ‚‡Ъ¸ ‚ВОЛ˜ЛМЫ I. й‰М‡НУ ˝ЪУ МВФ ‡‚ЛО¸МУ. СВОУ ‚ ЪУП, ˜ЪУ, ТУ„О‡Т- МУ Н‚‡МЪУ‚УИ ПВı‡МЛНВ, ‚ВОЛ˜ЛМ‡ ФВ В‰‡ММУИ ˝ОВН- Ъ УМЫ ˝МВ „ЛЛ МВ ПУКВЪ ·˚Ъ¸ УФ В‰ВОВМ‡ ЪУ˜МВВ БМ‡˜ВМЛfl T, ТОВ‰Ы˛˘В„У ЛБ ТУУЪМУ¯ВМЛfl ЙВИБВМ- ·В „‡ T $ "/ t, „‰В " – ФУТЪУflММ‡fl иО‡МН‡ Л t –

‚ ÂÏfl ‚Á‡ËÏÓ‰ÂÈÒÚ‚Ëfl. Ç˚·Â ÂÏ ‚ ͇˜ÂÒÚ‚Â ÓˆÂÌÍË t ˝ЩЩВНЪЛ‚МУВ ‚ ВПfl ‚Б‡ЛПУ‰ВИТЪ‚Лfl tm (6) Ë ÔÓÎÓ-

ÊËÏ Tmin = "/tm = "υ γ/(2bmax) = I, „‰Â bmax – χÍ- ÒËχθÌÓ Á̇˜ÂÌËÂ Ô ËˆÂθÌÓ„Ó Ô‡ ‡ÏÂÚ ‡, Ô Ë

НУЪУ УП ˝ОВНЪ УМЫ В˘В ПУКВЪ ·˚Ъ¸ ФВ В‰‡М‡ ˝МВ - „Лfl, ‰УТЪ‡ЪУ˜М‡fl ‰Оfl ‚УБ·ЫК‰ВМЛfl ЛОЛ ЛУМЛБ‡ˆЛЛ ‡ЪУП‡. зУ У„ ‡МЛ˜ВМЛВ У·О‡ТЪЛ Ф ЛˆВО¸М˚ı Ф‡ ‡- ПВЪ У‚, ТУ„О‡ТМУ ‰ Ы„УПЫ ТУУЪМУ¯ВМЛ˛ ЙВИБВМ·В - „‡ py y $ ", Ф Л‚У‰ЛЪ Н МВУФ В‰ВОВММУТЪЛ ФУФВ-

В˜МУ„У ЛПФЫО¸Т‡ p0 $ "/(2bmax) ≈ I/(υγ). иУОУКЛП p0min = I /(υγ) = p0min . íÓ„‰‡ ‰Îfl Tmin ÔÓÎÛ˜ËÏ ÓˆÂÌÍÛ Tmin = p20min ⁄ (2me ) = I2 ⁄ (2me υ2γ2). иУМЛП‡МЛВ ˝ЪУИ ˜‡ТЪЛ ОВНˆЛЛ ПУКВЪ ‚˚Б‚‡Ъ¸ М‡Л·УО¸¯ЛВ Ъ Ы‰МУТЪЛ Л ФУЪ В·У‚‡Ъ¸ БМ‡˜ЛЪВО¸МУ„У ‚ ВПВМЛ. зУ ВТОЛ ˜Л- Ъ‡ЪВО˛ ˝ЪУ Ы‰‡ОУТ¸, ЪУ, БМ‡˜ЛЪ, УМ ЫТ‚УЛО ТЫЪ¸ ТУУЪМУ¯ВМЛИ МВУФ В‰ВОВММУТЪЛ ЙВИБВМ·В „‡ Л М‡Ы˜ЛОТfl Ф ЛПВМflЪ¸ Лı ‰Оfl В¯ВМЛfl НУМН ВЪМ˚ı Б‡‰‡˜.

èÓ‰ÒÚ‡‚Ë‚ Á̇˜ÂÌË ‰Îfl Tmin ‚ ÙÓ ÏÛÎÛ (14) Ë Á‡- ÏÂÌË‚ υ ̇ β = υ/c, ÔÓÎÛ˜ËÏ

„‰Â re = e2 /(mec2) – ‚‚В‰ВММ˚И ‚˚¯В НО‡ТТЛ˜ВТНЛИ‡‰ЛЫТ ˝ОВНЪ УМ‡. и Л ‡Т˜ВЪВ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ ФЫЪ¸ ˜‡ТЪЛˆ˚ У·˚˜МУ ЛБПВ fl˛Ъ МВ ‚ Т‡МЪЛПВЪ ‡ı, ‡ ‚ „ ‡ПП‡ı М‡ Н‚‡‰ ‡ЪМ˚И Т‡МЪЛПВЪ („/ТП2). уЪУ·˚ ФУОЫ˜ЛЪ¸ ФОУЪМУТЪ¸ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ ‚ ˝ЪЛı В‰ЛМЛˆ‡ı, ТОВ‰ЫВЪ Ф ‡‚Ы˛ Л ОВ‚Ы˛ ˜‡ТЪЛ Ы ‡‚МВМЛfl (15) ФУ‰ВОЛЪ¸ М‡ ФОУЪМУТЪ¸ ‚В˘ВТЪ‚‡ ρ. н‡Н Н‡Н n = NAρ/A (NA – ˜ЛТОУ А‚У„‡- ‰ У), ЪУ (16) ПУКМУ Ф В‰ТЪ‡‚ЛЪ¸ ‚ ‚Л‰В

K = 4πr2e me c2 NA = 0,307 M˝Ç/(„/ÒÏ2).

л В‰МЛИ ЛУМЛБ‡ˆЛУММ˚И ФУЪВМˆЛ‡О I УФ В‰ВОflВЪТfl ˝НТФВ ЛПВМЪ‡О¸МУ. СОfl ˝ОВПВМЪУ‚ ЪflКВОВВ НЛТОУ-У‰‡ В„У ПУКМУ УˆВМЛЪ¸ ФУ ЩУ ПЫОВ (10 ± 1) Z ˝З. н‡Н Н‡Н ‰Оfl ·УО¸¯ЛМТЪ‚‡ ˝ОВПВМЪУ‚ Z/A = 1/2, ЪУ ФОУЪМУТЪ¸ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ ‚ ‚Л‰В (16) ТО‡·У Б‡‚ЛТЛЪ УЪ ЪЛФ‡ ‚В˘ВТЪ‚‡. З ˝ЪУП ТУТЪУflО ТП˚ТО ЛБПВ ВМЛfl Ф У·В„‡ ˜‡ТЪЛˆ˚ ‚ „/ТП2.

зВТНУО¸НУ ·УОВВ ЪУ˜МУВ ‚˚ ‡КВМЛВ ‰Оfl ФОУЪМУТЪЛ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸, НУЪУ УВ ¯Л УНУ ЛТФУО¸БЫВЪТfl ‚ М‡ТЪУfl˘ВВ ‚ ВПfl, ‰‡ВЪТfl ЩУ ПЫОУИ ЕВ- ЪВ–ЕОУı‡:

éÚ (16) ˝Ú‡ ÙÓ ÏÛ· ÓÚ΢‡ÂÚÒfl ˜ÎÂ̇ÏË β2 Ë δ/2. óÎÂÌ β2 Ы˜ЛЪ˚‚‡ВЪ ТОЫ˜‡Л ‡ТТВflМЛfl ВОflЪЛ‚ЛТЪТНУИ ˜‡ТЪЛˆ˚ Т ·УО¸¯ЛПЛ ФВ В‰‡˜‡ПЛ ˝МВ „ЛЛ (ТП. (11)). гВ„НУ УˆВМЛЪ¸, ˜ЪУ ı‡ ‡НЪВ МУВ БМ‡˜ВМЛВ ОУ- „‡ ЛЩП‡ ‚ (17) ‡‚МУ 30. иУ˝ЪУПЫ ФУФ ‡‚Н‡, Т‚flБ‡М- М‡fl Т ˜ОВМУП β2, ÌÂ Ô Â‚˚¯‡ÂÚ 10–15%.

уОВМ δ/2 ТЫ˘ВТЪ‚ВМ ‚ У·О‡ТЪЛ ЫО¸Ъ ‡ ВОflЪЛ‚ЛТЪТНЛı ˝МВ „ЛИ. и Л γ @ 1 П‡НТЛП‡О¸М‡fl ‚ВОЛ˜ЛМ‡ Ф‡-

‡ÏÂÚ ‡ bmax = "cγ/(2I) ≈ (γ/I [˝Ç]) 10−5 ТП (ТП. ‚˚- ¯В) ПУКВЪ ТЪ‡Ъ¸ БМ‡˜ЛЪВО¸МУ ·УО¸¯В ‡ТТЪУflМЛfl

ÏÂÊ‰Û ‡ÚÓχÏË ‚¢ÂÒÚ‚‡. Ç ˝ÚÓÏ ÒÎÛ˜‡Â ËÁ-Á‡ ÔÓÎfl-ËÁ‡ˆËË Ò Â‰˚ ÔÓΠ˜‡ÒÚˈ˚ ̇ ‡ÒÒÚÓflÌËflı bmax ·Ы‰ВЪ Б‡ПВЪМУ ПВМ¸¯В НЫОУМУ‚ТНУ„У Л Ы‚ВОЛ˜ВМЛВ

bmax Т УТЪУП ˝МВ „ЛЛ ˜‡ТЪЛˆ˚ Ф ВН ‡ЪЛЪТfl. щЪУЪ ˝ЩЩВНЪ Б‡‚ЛТЛЪ УЪ ФОУЪМУТЪЛ Т В‰˚ Л ˜‡ТЪУ М‡Б˚‚‡-

ВЪТfl ˝ЩЩВНЪУП ФОУЪМУТЪЛ. дУОЛ˜ВТЪ‚ВММУ УМ Ы˜Л- Ъ˚‚‡ВЪТfl ФУФ ‡‚НУИ δ/2. и Л γ @ 1 δ = 2ln(βγ Ч

× "ωp /I) − 1, „‰Â "ωp = 28,8 ρZ ⁄ A ˝З – ФО‡БПВММ‡fl ˝МВ „Лfl ‚В˘ВТЪ‚‡ (ρ ‚ „/ТП3).

л‰ВО‡ВП ‰‚‡ Б‡ПВ˜‡МЛfl. иВ ‚УВ Н‡Т‡ВЪТfl ЫТОУ- ‚Лfl МВФУ‰‚ЛКМУТЪЛ ‡ТТВЛ‚‡˛˘В„У ˆВМЪ ‡, ЪУ ВТЪ¸ ˝ОВНЪ УМ‡. й˜В‚Л‰МУ, ˜ЪУ ФУПЛПУ У„ ‡МЛ˜ВМЛИ М‡ У·О‡ТЪ¸ Ы„ОУ‚ ‡ТТВflМЛfl Л ‰Л‡Ф‡БУМ Ф ЛˆВО¸М˚ı Ф‡ ‡ПВЪ У‚, ‡ТТПУЪ ВММ˚ı ‚ ‡Б‰ВОВ 3, ‰УОКМУ ‚˚- ФУОМflЪ¸Тfl МВ ‡‚ВМТЪ‚У υ > υa , ÚÓ ÂÒÚ¸ ÒÍÓ ÓÒÚ¸ ˜‡Ò- Úˈ˚ ‰ÓÎÊ̇ Ô Â‚˚¯‡Ú¸ Ò Â‰Ì˛˛ ÒÍÓ ÓÒÚ¸ ˝ÎÂÍ- Ú ÓÌÓ‚ ‚ ‡ÚÓÏ υa Zαc, „‰Â α = e2 /("c) . 1/137 – ФУТЪУflММ‡fl ЪУМНУИ ТЪ ЫНЪЫ ˚. С Ы„УВ Б‡ПВ˜‡МЛВ Н‡Т‡ВЪТfl Ф УıУК‰ВМЛfl ˜‡ТЪЛˆ ˜В ВБ ‚В˘ВТЪ‚‡ ТУ ТПВТ¸˛ ‡ЪУПУ‚ Т ‡БОЛ˜М˚ПЛ A Ë Z. З ˝ЪУП ТОЫ˜‡В ‰Оfl ‚˚˜ЛТОВМЛfl ФОУЪМУТЪЛ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ У·˚˜МУ ФУО¸БЫ˛ЪТfl Ф ‡‚ЛОУП Е В„„‡: (−dE/ρdx) = = ∑w j (–dE ⁄ ρdx)j , „‰Â wj = ρj /ρ – ÓÚÌÓ¯ÂÌË ÔÎÓÚ-

j

МУТЪЛ j-„У ˝ОВПВМЪ‡ ‚ ТОУКМУП ‚В˘ВТЪ‚В Н ФОУЪМУТЪЛ j-„У ˝ОВПВМЪ‡, ‡ (−dE/ρdx)j – ФОУЪМУТЪ¸ ЛУМЛБ‡- ˆЛУММ˚ı ФУЪВ ¸ ‚ Т В‰В, ТУТЪУfl˘ВИ ЛБ j-„У ˝ОВПВМЪ‡.

6.бДЗалаейлнъ игйнзйлна айзабДсайззхп ийнЦкъ йн щзЦкЙаа уДлнасх

кВБЫО¸Ъ‡Ъ˚ ‡Т˜ВЪ‡ Б‡‚ЛТЛПУТЪЛ ФОУЪМУТЪЛ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ УЪ ˝МВ „ЛЛ ФУ ЩУ ПЫОВ (17) ФУН‡Б‡М˚ М‡ ЛТ. 4. Е˚ТЪ ˚И УТЪ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ Т ЫПВМ¸¯ВМЛВП ˝МВ „ЛЛ ‚ МВ ВОflЪЛ‚ЛТЪТНУИ У·О‡ТЪЛ βγ < 1 ЩЛБЛ˜ВТНЛ Т‚flБ‡М Т УТЪУП ФВ В‰‡М- МУ„У ЛПФЫО¸Т‡ p0 Б‡ Т˜ВЪ Ы‚ВОЛ˜ВМЛfl ˝ЩЩВНЪЛ‚МУ„У

êËÒ. 4. ᇂЛТЛПУТЪ¸ ФОУЪМУТЪЛ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ УЪ ‚ВОЛ˜ЛМ˚ βγ = pc/M, „‰Â p – ЛПФЫО¸Т Л M – П‡ТТ‡ ˜‡ТЪЛˆ˚. кЛТЫМУН Б‡ЛПТЪ‚У‚‡М ЛБ ‡·УЪ˚ [3]

‚ ВПВМЛ ‚Б‡ЛПУ‰ВИТЪ‚Лfl tm (6) Ф Л ЫПВМ¸¯ВМЛЛ ТНУ УТЪЛ ˜‡ТЪЛˆ˚. кУТЪ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ‚ВОflЪЛ‚ЛТЪТНУИ У·О‡ТЪЛ β ≈ c Ô ÓËÒıÓ‰ËÚ lnγ2 Á‡ Ò˜ÂÚ ‡Ò¯Ë ÂÌËfl ӷ·ÒÚË Ô ËˆÂθÌ˚ı Ô‡ ‡ÏÂÚ Ó‚

(bmax γ) Ë Û‚Â΢ÂÌËfl Tmax γ2 (ТП. ‡Б‰ВО 2). з‡НУМВˆ, ‚ ЫО¸Ъ ‡ ВОflЪЛ‚ЛТЪТНУИ (γ @ 1) У·О‡ТЪЛ ˝МВ „ЛИ

‚Â΢Ë̇ bmax У„ ‡МЛ˜Л‚‡ВЪТfl ˝ЩЩВНЪУП ФОУЪМУТЪЛ Л ОУ„‡ ЛЩПЛ˜ВТНЛИ УТЪ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ УФ В‰ВОflВЪТfl ЪУО¸НУ ‚ВОЛ˜ЛМУИ Tmax ≈ E.

д‡Н ‚Л‰МУ ЛБ ЛТ. 4, ФОУЪМУТЪ¸ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ ПЛМЛП‡О¸М‡ Ф Л БМ‡˜ВМЛflı βγ УЪ 3 ‰У 4. еЛМЛП‡О¸М˚В БМ‡˜ВМЛfl (−dE/ρdx) ‰Îfl ‡ÁÌ˚ı Ò Â‰ ̇ıÓ‰flÚÒfl ‚ ‰Ë‡Ô‡ÁÓÌ ÓÚ 1 ‰Ó 2 å˝Ç/(„/ÒÏ2), 1 å˝Ç = 106 ˝Ç. àÒÍβ˜ÂÌË ÒÓÒÚ‡‚ÎflÂÚ ‚Ó‰Ó Ó‰,

‰Îfl ÍÓÚÓ Ó„Ó (−dE/ρdx)min ≈ 4 å˝Ç/(„/ÒÏ2). ë‚flÁ‡ÌÓ ˝ÚÓ Ò ÚÂÏ, ˜ÚÓ ‰Îfl ‚Ó‰Ó Ó‰‡ Z/A = 1, ‡ Ì 1/2, Í‡Í ‰Îfl

·УО¸¯ЛМТЪ‚‡ ˝ОВПВМЪУ‚. бМ‡˜ВМЛfl (−dE/ρdx)min ‰Оfl‡БМ˚ı ‚В˘ВТЪ‚ ПУКМУ М‡ИЪЛ ‚ ‡·УЪВ [3].

7. бДдгыуЦзаЦ

й„ ‡МЛ˜ВММ˚И ‡БПВ ТЪ‡Ъ¸Л МВ ФУБ‚УОЛО Уı‚‡- ЪЛЪ¸ ‚‡КМ˚В ‚УФ УТ˚, Т‚flБ‡ММ˚В Т ЛУМЛБ‡ˆЛУММ˚- ПЛ ФУЪВ flПЛ ˝МВ „ЛЛ. д МЛП УЪМУТЛЪТfl Ф ВК‰В ‚ТВ„У Ф УıУК‰ВМЛВ Б‡ flКВММ˚ı ˜‡ТЪЛˆ ˜В ВБ Н ЛТЪ‡ОО˚ ФУ‰ П‡О˚ПЛ Ы„О‡ПЛ ФУ УЪМУ¯ВМЛ˛ Н УТЛ Н ЛТЪ‡ОО‡. з‡¯ ‚˚‚У‰ ЩУ ПЫО˚ ‰Оfl (−dE/ρdx), УТМУ‚‡ММ˚И М‡ ТОЫ˜‡ИМУП ‡ТФУОУКВМЛЛ ‡ТТВЛ‚‡˛˘Лı ˆВМЪ-У‚ УЪМУТЛЪВО¸МУ Ъ ‡ВНЪУ ЛЛ ˜‡ТЪЛˆ˚ ( ЛТ. 3), ‰Оfl ˝ЪУ„У ТОЫ˜‡fl МВ ФУ‰ıУ‰ЛЪ, Л ‚ВОЛ˜ЛМ‡ ЛУМЛБ‡ˆЛУМ- М˚ı ФУЪВ ¸ ˝МВ „ЛЛ ПУКВЪ УЪОЛ˜‡Ъ¸Тfl УЪ ‡ТТ˜ЛЪ‡М- МУИ ФУ ЩУ ПЫОВ ЕВЪВ–ЕОУı‡. З ˜‡ТЪМУТЪЛ, Ф Л Б‡- ı‚‡ЪВ ˜‡ТЪЛˆ˚ ‚ ВКЛП Н‡М‡ОЛ У‚‡МЛfl, ЪУ ВТЪ¸ Ф Л ВВ ‰‚ЛКВМЛЛ ПВК‰Ы Н ЛТЪ‡ООЛ˜ВТНЛПЛ ФОУТНУТЪflПЛ,

ЛУМЛБ‡ˆЛУММ˚В ФУЪВ Л УН‡Б˚‚‡˛ЪТfl Ф ЛПВ МУ ‚‰‚УВ ПВМ¸¯В, ˜ВП ‚ ‡ПУ ЩМУП ‚В˘ВТЪ‚В.

С Ы„ЛП ‚‡КМ˚П ‚УФ УТУП fl‚Оfl˛ЪТfl ЩОЫНЪЫ‡ˆЛЛ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ ˝МВ „ЛЛ. и УˆВТТ ТЪУОНМУ- ‚ВМЛfl ˜‡ТЪЛˆ Т ФВ В‰‡˜ВИ ‰‡ММУИ ˝МВ „ЛЛ fl‚ОflВЪТfl ТОЫ˜‡ИМ˚П. иУ˝ЪУПЫ ВТОЛ ‚ Т В‰Ы ФУФ‡‰‡ВЪ ФУЪУН ПУМУ˝МВ „ВЪЛ˜ВТНЛı ˜‡ТЪЛˆ, ЪУ ФУТОВ Ф УıУК‰ВМЛfl Т В‰˚ ˝МВ „ЛЛ ˜‡ТЪЛˆ ·Ы‰ЫЪ ‡БОЛ˜М˚. йН‡Б˚‚‡ВЪТfl, ˜ЪУ ‰Оfl ВОflЪЛ‚ЛТЪТНЛı ˜‡ТЪЛˆ ‡ТФ В‰ВОВМЛВ ФУ ˝МВ „ЛflП ·Ы‰ВЪ МВ „‡ЫТТУ‚˚П, ‡ БМ‡˜ЛЪВО¸МУ ·УОВВ ¯Л УНЛП Л ‡ТЛППВЪ Л˜М˚П, ·ОЛБНЛП Н Ъ‡Н М‡Б˚‚‡В- ПУПЫ ‡ТФ В‰ВОВМЛ˛ г‡М‰‡Ы. л‚flБ‡МУ ˝ЪУ Т ‚УБПУКМУТЪ¸˛ ФВ В‰‡˜Л БМ‡˜ЛЪВО¸МУИ ˝МВ „ЛЛ ˝ОВНЪ УМЫ ‚ У‰МУП ТЪУОНМУ‚ВМЛЛ (ТП. ‡Б‰ВО 2). оОЫНЪЫ‡ˆЛЛ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ УН‡Б˚‚‡˛Ъ ТЫ˘ВТЪ‚ВММУВ ‚ОЛflМЛВ М‡ ‡·УЪЫ Л ı‡ ‡НЪВ ЛТЪЛНЛ ЛУМЛБ‡ˆЛУМ- М˚ı ‰ВЪВНЪУ У‚ ˜‡ТЪЛˆ.

аМЪВ ВТМУИ Т‡ПУТЪУflЪВО¸МУИ Ф У·ОВПУИ fl‚ОflВЪТfl Ф УıУК‰ВМЛВ ПВ‰ОВММ˚ı (υ < υa ) ПМУ„УБ‡ fl‰- М˚ı ЛУМУ‚ ˜В ВБ ‚В˘ВТЪ‚У. иУОЫ˜ВММ˚В ‚˚¯В ЩУ - ПЫО˚ МВФ ЛПВМЛП˚ ‚ ˝ЪУП ТОЫ˜‡В.

ᇂЛТЛПУТЪ¸ ФОУЪМУТЪЛ ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ ¸ УЪ ˝МВ „ЛЛ ˜‡ТЪЛˆ˚ ПУКМУ ЛТФУО¸БУ‚‡Ъ¸ ‰Оfl ‡Т˜В- Ъ‡ ВВ Ф У·В„‡ ‚ ‚В˘ВТЪ‚В. бМ‡МЛВ ˝ЪУИ ‚ВОЛ˜ЛМ˚ fl‚- ОflВЪТfl ‚‡КМ˚П ‰Оfl ‡Т˜ВЪУ‚ ·ЛУОУ„Л˜ВТНУИ Б‡˘ЛЪ˚ ЛТЪУ˜МЛНУ‚ ЛБОЫ˜ВМЛfl Л Ф ЛПВМВМЛfl ФЫ˜НУ‚ ˜‡Т- ЪЛˆ ‚ ПВ‰ЛˆЛМВ.

нВП ЛБ ˜ЛЪ‡ЪВОВИ, НЪУ Б‡ıУ˜ВЪ ФУОЫ˜ЛЪ¸ ·УО¸¯В ЛМЩУ П‡ˆЛЛ У· ЛУМЛБ‡ˆЛУММ˚ı ФУЪВ flı ˝МВ „ЛЛ Л

ЛУМЛБ‡ˆЛУММ˚ı ‰ВЪВНЪУ ‡ı ˜‡ТЪЛˆ, ВНУПВМ‰ЫВП У· ‡ЪЛЪ¸Тfl Н ПУМУ„ ‡ЩЛЛ [4].

ганЦкДнмкД

1.ЙУО¸‰‡МТНЛИ З.а., зЛНЛЪЛМ ы.и., кУБВМЪ‡О¸ а.г. дЛМВП‡ЪЛ˜ВТНЛВ ПВЪУ‰˚ ‚ ЩЛБЛНВ ‚˚ТУНЛı ˝МВ „ЛИ. е.: з‡ЫН‡, 1987. л. 85–92.

2.ã‡Ì‰‡Û ã.Ñ., ãËٯˈ Ö.å. нВУ Лfl ФУОfl. е.: Йаоег, 1960. л. 116.

3.Barnett R.M. et al. Review of Particle Physics // Phys. Rev. D. 1966. Vol. 54, ‹ 1. P. 72, 132.

4.ÅÛ‰‡„Ó‚ û.А., å ÁÓÌ É.à., ëËÚ‡ Å., ó˜ËÌ Ç.А. аУМЛБ‡ˆЛУММ˚В ЛБПВ ВМЛfl ‚ ЩЛБЛНВ ‚˚ТУНЛı ˝МВ „ЛИ. е.: щМВ „У‡ЪУПЛБ‰‡Ъ, 1988.

* * *

лВ „ВИ иВЪ У‚Л˜ СВМЛТУ‚, Ф УЩВТТУ Н‡ЩВ‰ ˚ ЩЛБЛНЛ ˝ОВПВМЪ‡ М˚ı ˜‡ТЪЛˆ ЩЛБЛ˜ВТНУ„У Щ‡- НЫО¸ЪВЪ‡ еЙм, М‡˜‡О¸МЛН УЪ‰ВО‡ МВИЪ ЛММУИ ЩЛБЛНЛ аМТЪЛЪЫЪ‡ ЩЛБЛНЛ ‚˚ТУНЛı ˝МВ „ЛИ, ˜ОВМ-НУ -ВТФУМ‰ВМЪ кАз. м˜‡ТЪМЛН УЪН ˚ЪЛИ П‡Т¯Ъ‡·МУИ ЛМ‚‡ Л‡МЪМУТЪЛ ‚ УК‰ВМЛЛ ‡‰ УМУ‚, УТЪ‡ ФУО- М˚ı ТВ˜ВМЛИ ‡‰ УММ˚ı ‚Б‡ЛПУ‰ВИТЪ‚ЛИ, ‡МЪЛ„В- ОЛfl-3 Л t-Н‚‡ Н‡. г‡Ы В‡Ъ гВМЛМТНУИ Ф ВПЛЛ. лУ- ‡‚ЪУ ·УОВВ 200 ФЫ·ОЛН‡ˆЛИ.