
Принципы квантовой механики
Квантовый принцип суперпозиции
Самый непостижимый принцип. Он говорит, что в природе состояния представляют собой смесь состояний. Например, состояние частицы с определенной энергией внутри бесконечно глубокой потенциальной ямы представляет собой смесь состояний с импульсом, направленным к одной стенке, и импульсом, направленным к другой. Кажется, что это противоречит здравому смыслу. Частица движется сразу в противоположных направлениях. Но только это утверждение согласуется с требованием недостижимости области вне ямы.
Наиболее
поразительно квантовый принцип
суперпозиции проявляется в физике
элементарных частиц. Экспериментальные
исследования показали, что каждая
частица имеет некоторые свойства,
которые сохраняются в любых условиях,
подобно электрическому заряду, поэтому
часто эти свойства называют зарядами.
Одно из свойств назвали странностью.
Частицы, имеющие разную странность,
являются разными частицами. Например,
нейтральный каон
 и
его античастица
и
его античастица
 являются
разными частицами, поскольку их странный
заряд имеет противоположный знак. То,
что это разные частицы, говорит следующий
экспериментальный факт: при столкновении
антикаона
с протоном возможно такое превращение
p0
0.
Но никогда не бывает такого –
p0
0.
Название странность обязано тому, что
данный заряд сохраняется почти
всегда. Он не сохраняется в слабых
взаимодействиях. Нейтральный каон и
антикаон одинаково распадаются на
нестранные частицы:
являются
разными частицами, поскольку их странный
заряд имеет противоположный знак. То,
что это разные частицы, говорит следующий
экспериментальный факт: при столкновении
антикаона
с протоном возможно такое превращение
p0
0.
Но никогда не бывает такого –
p0
0.
Название странность обязано тому, что
данный заряд сохраняется почти
всегда. Он не сохраняется в слабых
взаимодействиях. Нейтральный каон и
антикаон одинаково распадаются на
нестранные частицы:
 и
и
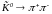 .
Это приводит к тому, что
и
могут превращаться друг в друга. Это
наблюдалось в эксперименте. Виновником
является квантовый принцип суперпозиции.
.
Это приводит к тому, что
и
могут превращаться друг в друга. Это
наблюдалось в эксперименте. Виновником
является квантовый принцип суперпозиции.
Фазовое пространство
Еще одно проявление квантового принципа суперпозиции приводит еще к одному очень важному принципу.
В классической механике состояние частицы определяется заданием координат и импульса. Например, при одномерном движении частицы пара x, px полностью определяют состояние в любой момент времени. Пространство, на координатных осях которого откладываются координаты и импульсы называется фазовым пространством. При движении x и px изменяются, частица описывает траекторию в фазовом пространстве. Например, имеем гармонический осциллятор массы m, с жесткостью k. При отсутствии трения его энергия сохраняется, поэтому справедливо:
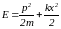 (1)
(1)
Закон сохранение энергии задает связь между координатой и импульсом. Уравнение (1) можно рассматривать как уравнение траектории в фазовом пространстве. Преобразуем:
 (2)
(2)
Уравнение
походит на уравнение эллипса с полуосями:
по оси OX
–
 ,
по оси OY
–
,
по оси OY
–
 .
.

В классической механике частица в каждый момент времени находится в некоторой точке фазового пространства.
В квантовой механике утверждается, что
в каждый момент времени квантовое
состояние частицы представляет собой
смесь классических состояний. Частица
занимает сразу некоторую область
фазового пространства размером x
на p.
В этом состоит принцип неопределенностей.
Природа так устроена, что в одно мгновение
невозможно точно определить где находится
частица и какой импульс она при этом
имеет.
квантовой механике утверждается, что
в каждый момент времени квантовое
состояние частицы представляет собой
смесь классических состояний. Частица
занимает сразу некоторую область
фазового пространства размером x
на p.
В этом состоит принцип неопределенностей.
Природа так устроена, что в одно мгновение
невозможно точно определить где находится
частица и какой импульс она при этом
имеет.
