33

Введение

Математическое моделирование – могучее средство изучения природы, техники и человеческого общества. Что такое модель? Слово «модель» в переводе с итальянского означает «копия, образец, прототип». Изучив модель, мы познаем оригинал. Значит, математическая модель – это прототип какой-то части мира – объекта, системы, устройства, машины, процесса, прибора, изучая который, мы постигаем эту часть мира. Мы будем рассматривать математические модели в относительно узкой области – механике упругого тела.

При расчете напряженно-деформированного состояния инженерных сооружений приходится иметь дело не с самим сооружением, а с его расчетной моделью. Физическая модель сооружения (расчетная схема) получается путем принятия некоторых упрощающих гипотез, не оказывающих заметного влияния на реальное поведение сооружения. Математическая модель описывает поведение физической модели с помощью определенных соотношений, связывающих между собой параметры, определяющие такое поведение. В качестве параметров могут выступать геометрические размеры, жесткостные характеристики, деформации, перемещения, усилия, напряжения и т. п. Например, для определения перемещений и усилий от собственного веса Останкинской телебашни (рис. 1а) можно использовать очень простую физическую модель – прямолинейный стержень, подвергающийся действию переменной распределенной нагрузки (см. рис. 2).

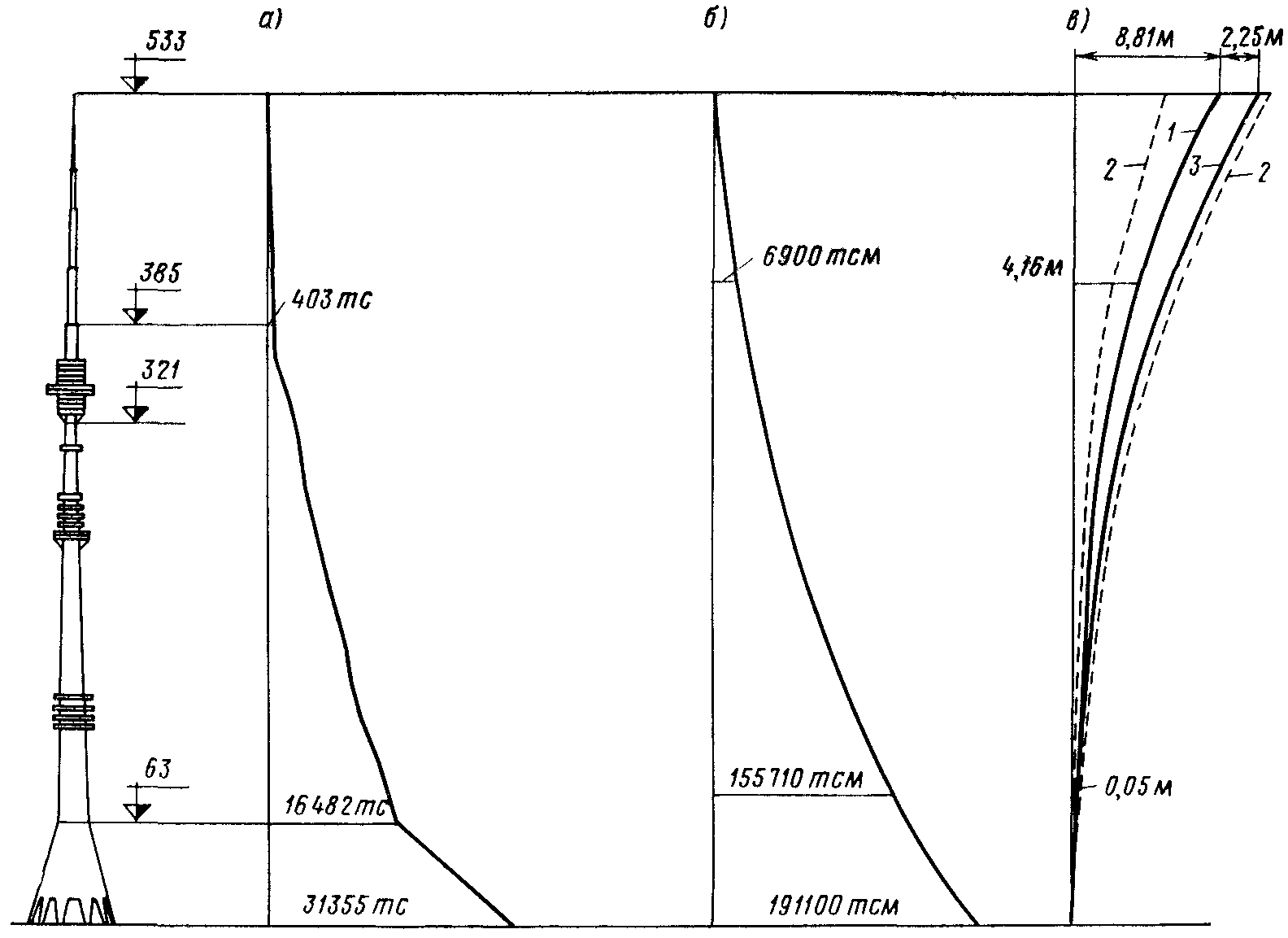
Рис. 1. Изменение продольных усилий от собственного веса (а), изгибающих моментов (б) и прогибов (в) от ветровой нагрузки по высоте Останкинской телебашни

Рис. 2. Физическая модель (расчетная схема)

Математическая модель будет фигурировать в виде дифференциального уравнения

,

включающего перемещение u(x), распределенную переменную по координате x нагрузку q(x) и продольную жесткость ЕА(x) (Е – модуль упругости материала, А(x) – площадь сечения). При этом продольное усилие N(x) и перемещение u(x) связаны между собой соотношением

.

Решение этой математической модели дает функцию перемещений и внутренних усилий, т. е. напряженно-деформированное состояние физической модели.

Лекция 1

Типы уравнений в механике твердого деформируемого тела

Рассмотрим построение математической модели для простейшего случая растяжения-сжатия стержня (рис. 2).

При решении задач механики твердого тела используются три типа уравнений:

1 – уравнения равновесия;

2 – деформационные соотношения;

3 – физические соотношения.

Эти уравнения получаются следующим образом.

1. Уравнения равновесия :

• вырезается (мысленно) бесконечно малый элемент (у стержня – линейный длиной dx (рис. 3), у пластин и оболочек – плоский или искривленный прямоугольник c размерами dx, dy, у монолитных конструкций – параллелепипед со сторонами dx, dy, dz);

• по местам разреза прикладываются неизвестные внутренние усилия и моменты (в нашем случае только продольные усилия N);

• рассматриваются условия равновесия элемента.

Рис. 3. Бесконечно малый элемент стержня.

Запишем уравнение равновесия (сумму проекций на ось x)

.

Деля на dx, получим:

. (1)

Таким образом, уравнения равновесия связывают между собой в дифференциальной форме внутренние силовые факторы и внешнюю нагрузку.

2. Деформационные соотношения получаются из рассмотрения деформированного состояния элемента.

Рисунок 4. Деформация бесконечно малого элемента

Длина недеформированного элемента:

.

Длина его после деформирования:

.

Относительная (безразмерная) деформация:

. (2)

Таким образом, деформационные соотношения связывают между собой в дифференциальной форме деформации и перемещения

3. Интегрируя по площади закон Гука:

,

где Е – модуль упругости материала, - напряжение, и учитывая, что в случае растяжения-сжатия деформации в сечении постоянны, приходим к соотношению:

. (3)

Таким образом, физические соотношения связывают между собой в алгебраической форме внутренние силовые факторы и деформации.

Внося в физические соотношения деформационные соотношения, получаем связь между внутренними силовыми факторами и перемещениями (соотношения Коши). В нашем случае

. (4)

Наконец, после внесения соотношений Коши в уравнения равновесия, приходим к уравнению упругого равновесия :

,

или, после деления на жесткость растяжения – сжатия EА:

. (5)

Это уравнение и предстоит решать различными способами.