Современные проблемы физики / PhysicalReviewpdf / Soifer-1

© лУИЩВ З.Д., 1999

110

COMPUTER OPTICS Part 1. Diffractive optical elements

V. A. SOIFER

The fundamentals of designing Diffractive Optical Elements (DOEs) with wide functional capabilities are described. Various approaches and techniques for obtaining zone plates with complex microrelief are set forth. The equations that describe the boundaries and profile of the zones are discussed. Illustrated examples of planar, spherical and cylindrical lenses, a planar prism and reflecting focusators are considered.

аБО‡„‡˛ЪТfl УТМУ‚˚ ТУ- Б‰‡МЛfl ‰ЛЩ ‡НˆЛУММ˚ı УФЪЛ˜ВТНЛı ˝ОВПВМЪУ‚ (Сйщ) Т ¯Л УНЛПЛ ЩЫМНˆЛУМ‡О¸М˚ПЛ ‚УБПУКМУТЪflПЛ. й·ТЫК‰‡˛ЪТfl ФЫЪЛ Л ПВЪУ‰˚ ФУОЫ˜В- МЛfl БУМЛ У‚‡ММ˚ı ФО‡Т- ЪЛМУН ТУ ТОУКМ˚П Ф У- ЩЛОВП БУМ. ДМ‡ОЛБЛ Ы- ˛ЪТfl Ы ‡‚МВМЛfl „ ‡МЛˆ Л Ф УЩЛОfl БУМ. З Н‡˜В- ТЪ‚В Ф ЛПВ У‚ ‡ТТП‡Ъ-Л‚‡˛ЪТfl ФОУТНЛВ ТЩВ-Л˜ВТНЛВ Л ˆЛОЛМ‰ Л˜В- ТНЛВ ОЛМБ˚, ФОУТН‡fl Ф ЛБП‡, УЪ ‡К‡˛˘ЛВ ЩУНЫТ‡ЪУ ˚.

дйеиъынЦкзАь йинадА у‡ТЪ¸ 1. СЛЩ ‡НˆЛУММ˚В УФЪЛ˜ВТНЛВ ˝ОВПВМЪ˚

З. Д. лйвоЦк

л‡П‡ ТНЛИ „УТЫ‰‡ ТЪ‚ВММ˚И ‡˝ УНУТПЛ˜ВТНЛИ ЫМЛ‚В ТЛЪВЪ ЛП. л.и. дУ УОВ‚‡

ЗЗЦСЦзаЦ

и В‰ПВЪУП ‡ТТПУЪ ВМЛfl ˝ЪУИ ТЪ‡Ъ¸Л fl‚ОflВЪТfl МУ‚‡fl У·О‡ТЪ¸ БМ‡МЛИ, ЪВ ПЛМУОУ„Лfl ‚ НУЪУ УИ В˘В ‰У НУМˆ‡ МВ ЫТЪ‡МУ‚ЛО‡Т¸. к‡БМ˚В ‡‚ЪУ ˚ ЛТФУО¸БЫ- ˛Ъ ‡БОЛ˜М˚В М‡Б‚‡МЛfl: “НУПФ¸˛ЪВ М‡fl УФЪЛН‡”, “УФЪЛН‡, ТЛМЪВБЛ У‚‡ММ‡fl НУПФ¸˛ЪВ УП”, “·ЛМ‡ - М‡fl УФЪЛН‡”, “ФОУТН‡fl УФЪЛН‡”, “‰ЛЩ ‡НˆЛУММ‡fl УФЪЛН‡” Л Ъ.‰. З О˛·УП ТОЫ˜‡В В˜¸ Л‰ВЪ У· УФЪЛ˜ВТНЛı ˝ОВПВМЪ‡ı, ‡БОЛ˜М˚В УЪОЛ˜ЛЪВО¸М˚В УТУ·ВММУТЪЛ НУЪУ ˚ı ‡ТН ˚‚‡˛ЪТfl ФВ В˜ЛТОВММ˚ПЛ М‡- Б‚‡МЛflПЛ.

ЗМВ¯МВ Ъ‡НУИ УФЪЛ˜ВТНЛИ ˝ОВПВМЪ Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ Ф УФЫТН‡˛˘Ы˛ ЛОЛ УЪ ‡К‡˛˘Ы˛ ФО‡ТЪЛМНЫ Т ЪУМНЛП Щ‡БУ‚˚П ПЛН У ВО¸ВЩУП, ‡ТТ˜ЛЪ‡ММ˚П ‚ ‡ПН‡ı ЪВУ ЛЛ ‰ЛЩ ‡НˆЛЛ. иВ ‚˚П Ф В‰ТЪ‡‚ЛЪВОВП ˝ЪУ„У НО‡ТТ‡ УФЪЛ˜ВТНЛı ˝ОВПВМЪУ‚ fl‚ОflВЪТfl ‰ЛЩ ‡НˆЛУММ‡fl В¯ВЪН‡, ТУБ‰‡ММ‡fl ·УОВВ 200 ОВЪ ЪУПЫ М‡Б‡‰, Б‡‰УО„У ‰У ФУfl‚ОВМЛfl НУПФ¸˛ЪВ У‚. лОВ‰Ы˛˘ЛП ФУ ı УМУОУ„ЛЛ Ф В‰ТЪ‡‚ЛЪВОВП ЫН‡Б‡М- МУ„У НО‡ТТ‡ УФЪЛ˜ВТНЛı ˝ОВПВМЪУ‚ fl‚ОflВЪТfl БУММ‡fl ФО‡ТЪЛМН‡. щЪЛ ‰ЛЩ ‡НˆЛУММ˚В УФЪЛ˜ВТНЛВ ˝ОВПВМЪ˚ (Сйщ) ЛПВОЛ ·ЛМ‡ МУВ ‡ПФОЛЪЫ‰МУВ ЛОЛ Щ‡- БУ‚УВ Ф УФЫТН‡МЛВ. ЦТОЛ ‰ЛЩ ‡НˆЛУММ˚В В¯ВЪНЛ М‡¯ОЛ ¯Л УНУВ Ф ЛПВМВМЛВ ‚ Ф Л·У УТЪ УВМЛЛ, ЪУ БУММ˚В ФО‡ТЪЛМ˚ ‚ УТМУ‚МУП ЛТФУО¸БУ‚‡ОЛТ¸ ‚ Ы˜В·МУП О‡·У ‡ЪУ МУП Ф ‡НЪЛНЫПВ ФУ УФЪЛНВ ‰Оfl ЛОО˛ТЪ ‡ˆЛЛ ФУОУКВМЛИ ЪВУ ЛЛ ‰ЛЩ ‡НˆЛЛ.

з‡ТЪУfl˘Ы˛ В‚УО˛ˆЛ˛ ‚ ТУБ‰‡МЛЛ Сйщ Ф УЛБ- ‚ВОУ Ф ЛПВМВМЛВ НУПФ¸˛ЪВ У‚. и Л˜ВП ‚М‡˜‡ОВ, ‚ 70-ı „У‰‡ı, НУПФ¸˛ЪВ ˚ ТЪ‡ОЛ Ф ЛПВМflЪ¸ ‰Оfl ТЛМЪВ- Б‡ „УОУ„ ‡ПП П‡ЪВП‡ЪЛ˜ВТНЛ Б‡‰‡ММ˚ı У·˙ВНЪУ‚. и Л ˝ЪУП ·˚О‡ В¯ВМ‡ НО˛˜В‚‡fl Ф У·ОВП‡ НУ‰Л У- ‚‡МЛfl – Б‡ФЛТ¸ М‡ ЩЛБЛ˜ВТНЫ˛ Т В‰Ы НУПФОВНТМУБМ‡˜М˚ı ЩЫМНˆЛИ Л ФУОЫ˜ВМЛВ ТУУЪ‚ВЪТЪ‚Ы˛˘Лı ‡ПФОЛЪЫ‰МУ-Щ‡БУ‚˚ı Ъ ‡МТФ‡ ‡МЪУ‚. щЪУ ФУТОЫКЛОУ ЪУО˜НУП Н НУПФ¸˛ЪВ МУПЫ ТЛМЪВБЫ ·ЛМ‡ М˚ı ‡ПФОЛЪЫ‰МУ-Щ‡БУ‚˚ı Л Щ‡БУ‚˚ı Ф УТЪ ‡МТЪ‚ВММ˚ı ЩЛО¸Ъ У‚, ‰Оfl Б‡ФЛТЛ НУЪУ ˚ı М‡ ЩЛБЛ˜ВТНЫ˛ Т В‰Ы Ф ЛПВМflОЛТ¸ „ ‡ЩУФУТЪ УЛЪВОЛ, ‡ Б‡ЪВП Л ЩУЪУФУТЪ УЛЪВОЛ. З ВБЫО¸Ъ‡ЪВ Ф У„ ВТТ‡ ‚ У·О‡ТЪЛ ПЛН У- ˝ОВНЪ УМЛНЛ Л О‡БВ МУИ ЪВıМЛНЛ, НУЪУ ˚И Ф Л‚ВО Н ФУfl‚ОВМЛ˛ ‚ НУМˆВ 80-ı „У‰У‚ Ф ВˆЛБЛУММ˚ı ЩУЪУФУТЪ УЛЪВОВИ Л ˝ОВНЪ УММ˚ı ОЛЪУ„ ‡ЩУ‚, Ф ‡НЪЛ˜В- ТНЛ В‡ОЛБУ‚‡О‡Т¸ Б‡‰‡˜‡ ТУБ‰‡МЛfl ‰ЛЩ ‡НˆЛУММ˚ı УФЪЛ˜ВТНЛı ˝ОВПВМЪУ‚ ТУ ТОУКМ˚П Ф УЩЛОВП БУМ. ЗУБМЛНОУ ¯Л УНУВ ФУОВ ‰ВflЪВО¸МУТЪЛ ‰Оfl ЩЛБЛНУ‚,

лйкйлйЗлдав йЕкДбйЗДнЦгъзхв ЬмкзДг, ‹4, 1999

УФЪЛНУ‚, ТФВˆЛ‡ОЛТЪУ‚ ‚ У·О‡ТЪflı Ф ЛНО‡‰МУИ П‡- ЪВП‡ЪЛНЛ Л ˝ОВНЪ УМЛНЛ, ЪВıМУОУ„У‚, ТФВˆЛ‡ОЛТЪУ‚ ФУ ‡‚ЪУП‡ЪЛБ‡ˆЛЛ. иУfl‚ЛОЛТ¸ Сйщ Т ЫМЛН‡О¸М˚ПЛ ı‡ ‡НЪВ ЛТЪЛН‡ПЛ, МВ‰УТЪЛКЛП˚ПЛ ‚ ‡ПН‡ı Ъ ‡- ‰ЛˆЛУММУИ УФЪЛНЛ, М‡Ф ЛПВ ЩУНЫТ‡ЪУ ˚ О‡БВ МУ- „У ЛБОЫ˜ВМЛfl.

омздсайзДгъзхЦ ЗйбейЬзйлна бйзакйЗДззхп СаокДдсайззхп йинауЦлдап щгЦеЦзнйЗ

АПФОЛЪЫ‰М‡fl У‰МУПВ М‡fl (1D) ‰ЛЩ ‡НˆЛУММ‡flВ¯ВЪН‡ Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ ФОУТНЛИ Ъ ‡МТФ‡ ‡МЪ, М‡ НУЪУ УП ˜В В‰Ы˛ЪТfl Т‚ВЪО˚В Л ЪВПМ˚В Ф‡ ‡О- ОВО¸М˚В ФУОУТНЛ (¯Ъ ЛıЛ Л ˘ВОЛ). иУОУТНЛ ЛПВ˛Ъ У‰ЛМ‡НУ‚Ы˛ ¯Л ЛМЫ. ЦТОЛ УТ‚ВЪЛЪ¸ Ъ‡НЫ˛ В¯ВЪНЫ ПУМУı УП‡ЪЛ˜ВТНЛП ФЫ˜НУП Т‚ВЪ‡ Т ‰ОЛМУИ ‚УОМ˚ λ, Ф‡‰‡˛˘ЛП МУ П‡О¸МУ Н ФОУТНУТЪЛ В¯ВЪНЛ, ЪУ ‚ВБЫО¸Ъ‡ЪВ ‰ЛЩ ‡НˆЛЛ Т‚ВЪ‡ М‡ ФВ ЛУ‰Л˜ВТНУИ ТЪ ЫНЪЫ В ˘ВОВИ ·Ы‰ВЪ У· ‡БУ‚‡МУ ПМУКВТЪ‚У ФЫ˜- НУ‚ Т‚ВЪ‡, ‚˚ıУ‰fl˘Лı ФУ‰ ‡БОЛ˜М˚ПЛ Ы„О‡ПЛ αp Ë ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘Ëı ‡Á΢Ì˚Ï ÔÓ fl‰Í‡Ï ‰ËÙ ‡ÍˆËË. ì„ÓÎ αp Б‡‚ЛТЛЪ УЪ ФВ ЛУ‰‡ В¯ВЪНЛ Л ‚ Ф В‰ФУОУКВМЛЛ П‡ОУТЪЛ Ы„ОУ‚ УФ В‰ВОflВЪТfl ФУ ЩУ ПЫОВ

T – ФВ ЛУ‰ В¯ВЪНЛ. аМЪВМТЛ‚МУТЪ¸ Т‚ВЪ‡ Ы·˚‚‡ВЪ Т УТЪУП ‡·ТУО˛ЪМУИ ‚ВОЛ˜ЛМ˚ p. д‡Н ТОВ‰ЫВЪ ЛБ ЪВУ ЛЛ ‰ЛЩ ‡НˆЛУММ˚ı В¯ВЪУН, Ф Л ‡‚МУИ ¯Л-ЛМВ ¯Ъ Лı‡ Л ˘ВОЛ ı‡ ‡НЪВ Ы·˚‚‡МЛfl УФ В‰ВОflВЪТfl ЩУ ПЫОУИ

аБ-Б‡ ЪУ„У ˜ЪУ БМ‡˜ЛЪВО¸М‡fl ˜‡ТЪ¸ Т‚ВЪ‡ ФУ„ОУ- ˘‡ВЪТfl ‡ПФОЛЪЫ‰М˚П Ъ ‡МТФ‡ ‡МЪУП, ‰ЛЩ ‡НˆЛУМ- М‡fl ˝ЩЩВНЪЛ‚МУТЪ¸ ‚ ФВ ‚УП ФУ fl‰НВ МВ Ф В‚˚¯‡ВЪ 10%. м У‰МУПВ МУИ Щ‡БУ‚УИ ‰ЛЩ ‡НˆЛУММУИ В¯ВЪНЛ ˝ЪУЪ ФУН‡Б‡ЪВО¸ Ф Л·ОЛБЛЪВО¸МУ ‚ 4 ‡Б‡ ‚˚¯В.

оЫМНˆЛfl Ф УФЫТН‡МЛfl ‚ ‰‡ММУП ТОЫ˜‡В fl‚ОflВЪТfl ˜ЛТЪУ Щ‡БУ‚УИ, ФВ ЛУ‰Л˜ВТНУИ Т ФВ ЛУ‰УП T, ‡ „Ы- ПВМЪ НУЪУ УИ ТН‡˜НУУ· ‡БМУ ПВМflВЪТfl М‡ π. оЫМНˆЛУМ‡О¸МУ Щ‡БУ‚‡fl Л ‡ПФОЛЪЫ‰М‡fl ‰ЛЩ ‡НˆЛУММ˚ВВ¯ВЪНЛ У‰ЛМ‡НУ‚˚.

ЦТЪВТЪ‚ВММ˚П ‡Б‚ЛЪЛВП У‰МУПВ М˚ı ·ЛМ‡ - М˚ı ‡ПФОЛЪЫ‰М˚ı Л Щ‡БУ‚˚ı ‰ЛЩ ‡НˆЛУММ˚ı В- ¯ВЪУН fl‚Оfl˛ЪТfl ТУУЪ‚ВЪТЪ‚Ы˛˘ЛВ ‰‚ЫПВ М˚В (2D)‡‰Л‡О¸МУ-ТЛППВЪ Л˜М˚В В¯ВЪНЛ (БУММ˚В ФО‡Т- ЪЛМНЛ). з‡ ЛТ. 1 ФУН‡Б‡М ˆВМЪ ‡О¸М˚И Щ ‡„ПВМЪ БУММУИ ФО‡ТЪЛМНЛ к˝ОВfl–лУ ˝.

èÓflÒÌËÏ ÔÓÌflÚË ÁÓÌ˚. áÓ̇ – ˝ЪУ У„ ‡МЛ˜ВМ- М‡fl У·О‡ТЪ¸ Сйщ, М‡ НУЪУ УИ ЩЫМНˆЛfl Ф УФЫТН‡МЛfl Т‚ВЪ‡ Ф ВЪВ ФВ‚‡ВЪ У‰МУН ‡ЪМУВ ЛБПВМВМЛВ УЪ ПЛМЛП‡О¸МУ„У ‰У П‡НТЛП‡О¸МУ„У БМ‡˜ВМЛfl. СОfl ‡ПФОЛЪЫ‰МУИ ‰ЛЩ ‡НˆЛУММУИ В¯ВЪНЛ БУМ‡ Ф В‰ТЪ‡‚- ОflВЪ ТУ·УИ ТУ˜ВЪ‡МЛВ ЪВПМУИ Л Т‚ВЪОУИ ФУОУТ ‚ Ф В‰ВО‡ı У‰МУ„У ФВ ЛУ‰‡ В¯ВЪНЛ. Й ‡МЛˆ‡ БУМ Ф Л ˝ЪУП Ф flП‡fl ОЛМЛfl. СОfl БУММУИ ФО‡ТЪЛМНЛ к˝ОВfl–

êËÒ. 1. сВМЪ ‡О¸М˚И Щ ‡„ПВМЪ БУММУИ ФО‡ТЪЛМНЛ к˝ОВfl–лУ ˝

лУ ˝ БУМ‡ Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ ТУ‚УНЫФМУТЪ¸ ЪВПМУ- „У Л Т‚ВЪОУ„У НУОВˆ ФВ ВПВММУИ ЪУО˘ЛМ˚ ( ЛТ. 1). Й ‡МЛˆ‡ БУМ Ф Л ˝ЪУП УН ЫКМУТЪ¸ ФВ ВПВММУ„У ‰Л- ‡ПВЪ ‡.

ꇉЛЫТ˚ УН ЫКМУТЪЛ ПВМfl˛ЪТfl Ф УФУ ˆЛУМ‡О¸- МУ Н‚‡‰ ‡ЪМ˚П НУ МflП ЛБ ФУТОВ‰У‚‡ЪВО¸М˚ı ˆВО˚ı ˜ЛТВО p:

„‰Â f – ЩУНЫТМУВ ‡ТТЪУflМЛВ.

î ‡„ÏÂÌÚ 2D Щ‡БУ‚УИ БУММУИ ФО‡ТЪЛМНЛ ЛБУ·-‡КВМ М‡ ЛТ. 2.

бУММ‡fl ФО‡ТЪЛМН‡ ‚˚ФУОМflВЪ ЩЫМНˆЛ˛ ЩУНЫТЛ-У‚НЛ Т‚ВЪ‡ Л ‚В‰ВЪ ТВ·fl Н‡Н ОЛМБ‡ Т ПМУКВТЪ‚УП ЩУНЫТУ‚ f−2 , f−1 , f0 , f1 , f2 , ТУУЪ‚ВЪТЪ‚Ы˛˘Лı ‡БОЛ˜- М˚П ФУ fl‰Н‡П ‰ЛЩ ‡НˆЛЛ Л ‡ТФУОУКВММ˚ı М‡ УТЛ‡ТФ УТЪ ‡МВМЛfl Т‚ВЪ‡:

аМЪВМТЛ‚МУТЪ¸ Т‚ВЪ‡ Ы·˚‚‡ВЪ Т УТЪУП МУПВ ‡ ФУ-fl‰Н‡ ФУ Б‡НУМЫ

ëÓ‚Â ¯ÂÌÒÚ‚Ó‚‡ÌË ·‡ÁÓ‚˚ı Ñéù, ͇ÍËÏË fl‚- Îfl˛ÚÒfl 1D ‰ЛЩ ‡НˆЛУММ˚В В¯ВЪНЛ, ‚УБПУКМУ Б‡ Т˜ВЪ ЛБПВМВМЛfl Ф УЩЛОfl БУМ. и Л ˝ЪУП ФУОЫ˜‡˛ЪТfl Ъ‡Н М‡Б˚‚‡ВП˚В В¯ВЪНЛ Т ·ОВТНУП. з‡Ф ЛПВ , ПУКМУ ‡ТТПУЪ ВЪ¸ ‡ПФОЛЪЫ‰МЫ˛ 1D ‰ЛЩ ‡НˆЛУММЫ˛

êËÒ. 2. о ‡„ПВМЪ ·ЛМ‡ МУИ Щ‡БУ‚УИ БУММУИ ФО‡- ТЪЛМНЛ

В¯ВЪНЫ, ЩЫМНˆЛfl Ф УФЫТН‡МЛfl НУЪУ УИ ПВМflВЪТfl ФУ

2 πλx

Á‡ÍÓÌÛ cos 2 --T--- . è Ë ‰ËÙ ‡ÍˆËË Ì‡ Ú‡ÍÓÈ Â-

¯ВЪНВ ЪВУ ВЪЛ˜ВТНЛ ФУПЛПУ МЫОВ‚У„У У· ‡БЫ˛ЪТfl ЪУО¸НУ ±1 ФУ fl‰НЛ ‰ЛЩ ‡НˆЛЛ. и ‡НЪЛ˜ВТНЛ, Т Ы˜В- ЪУП ФУ„ В¯МУТЪВИ ЛБ„УЪУ‚ОВМЛfl Сйщ, ‰ВОУ У·ТЪУЛЪ „У ‡Б‰У ТОУКМВВ.

ÑÎfl ‰‚ÛÏ Ì˚ı (2D) ‰ЛЩ ‡НˆЛУММ˚ı В¯ВЪУН ВТЪВТЪ‚ВММ˚ПЛ fl‚Оfl˛ЪТfl ФУТЪ УВМЛВ БУМ, УЪОЛ˜- М˚ı УЪ ФВ ЛУ‰Л˜ВТНЛı ˘ВОВ- Л НУО¸ˆВУ· ‡БМ˚ı, Л ‚˚fl‚ОВМЛВ МУ‚˚ı ЩЫМНˆЛУМ‡О¸М˚ı ‚УБПУКМУТЪВИ Сйщ. зВТПУЪ fl М‡ Н‡КЫ˘Ы˛Тfl У˜В‚Л‰МУТЪ¸, Т ПУПВМЪ‡ ТУБ‰‡МЛfl БУММУИ ФО‡ТЪЛМНЛ ˝ЪУЪ ‚УФ УТ МВ ФУ‰МЛП‡ОТfl ‚ ЪВ˜ВМЛВ ПМУ„Лı ОВЪ ЛБ-Б‡ УЪТЫЪТЪ‚Лfl Ф ‡НЪЛ˜ВТНУИ ‚УБПУКМУТЪЛ В‡ОЛБ‡ˆЛЛ БУММ˚ı ФО‡ТЪЛМУН Т ‚‡ ¸Л ЫВП˚П ı‡ ‡НЪВ УП БУМ. н‡Н‡fl ‚УБПУКМУТЪ¸ ФУfl‚ЛО‡Т¸ ‚ Т‚flБЛ Т ТУБ‰‡МЛВП НУП- Ф¸˛ЪВ У‚ Л ЪВıМЛ˜ВТНЛı Т В‰ТЪ‚ П‡¯ЛММУИ „ ‡ЩЛНЛ, ‚ ˜‡ТЪМУТЪЛ „ ‡ЩУ- Л ЩУЪУФУТЪ УЛЪВОВИ.

А.З. гУП‡М Л С.и. и‡ ЛТ ‚ 1967 „У‰Ы Ф В‰ОУКЛОЛ 2D ‰ЛЩ ‡НˆЛУММ˚В В¯ВЪНЛ Т ‚‡ ¸Л ЫВП˚ПЛ БУМ‡- ПЛ о ВМВОfl, ФУОЫ˜‡ВП˚В М‡ УТМУ‚В ПЫ‡ У‚˚ı ˝Щ- ЩВНЪУ‚ ‚ ВБЫО¸Ъ‡ЪВ ТЫФВ ФУБЛˆЛЛ Ф‡ ˚ ТЛМЪВБЛ У- ‚‡ММ˚ı П‡ТУН. лЛМЪВБЛ У‚‡ММ˚В П‡ТНЛ ТУ‰В К‡Ъ ФВ ЛУ‰Л˜ВТНЛВ ФУ У‰МУИ ЛБ НУУ ‰ЛМ‡Ъ ( М‡Ф ЛПВ , ФУ x) ·ЛМ‡ М˚В ЛБУ· ‡КВМЛfl, УФЛТ˚‚‡ВП˚В ТФВˆЛ- ‡О¸МУ ФУ‰У· ‡ММУИ ‡О„В· ‡Л˜ВТНУИ ЩЫМНˆЛВИ ϕ(x, y). LJ ¸Ë Ûfl ‚ˉ Ë Ô‡ ‡ÏÂÚ ˚ ÙÛÌ͈ËË ϕ(x, y), ‡ Ъ‡НКВ Ф‡ ‡ПВЪ ˚ УЪМУТЛЪВО¸МУ Т‰‚Л„‡ x Л ФУ‚У УЪ‡ П‡- ТУН ПУКМУ ФУОЫ˜ЛЪ¸ ПМУКВТЪ‚У ‡ПФОЛЪЫ‰М˚ı 2D ‰ЛЩ ‡НˆЛУММ˚ı В¯ВЪУН, Н‡К‰УИ ЛБ НУЪУ ˚ı ·Ы‰ВЪ ТУУЪ‚ВЪТЪ‚У‚‡Ъ¸ Т‚Уfl Н‡ ЪЛМ‡ ‰ЛЩ ‡НˆЛЛ. д ТУК‡- ОВМЛ˛, УФЛТ‡ММ‡fl Ф УˆВ‰Ы ‡ ТУ‰В КЛЪ В„ЫОfl М˚И ПВЪУ‰ ТЛМЪВБ‡ ЪУО¸НУ ‰Оfl ˆЛОЛМ‰ Л˜ВТНЛı Л ТЩВ Л- ˜ВТНЛı БУМ о ВМВОfl. кВБЫО¸Ъ‡Ъ ЩУНЫТЛ У‚НЛ Ф В‰- ТЪ‡‚ОflВЪ ТУ·УИ Ф flПЫ˛ ЩУН‡О¸МЫ˛ ОЛМЛ˛. аПВВЪТfl Ъ‡НКВ ‚УБПУКМУТЪ¸ ФУТЪ УВМЛfl НУМЛ˜ВТНЛı БУММ˚ı ФО‡ТЪЛМУН ФЫЪВП УФЪЛ˜ВТНУИ В„ЛТЪ ‡ˆЛЛ ВБЫО¸Ъ‡- Ъ‡ ЩЛБЛ˜ВТНУИ ТЫФВ ФУБЛˆЛЛ ˆЛОЛМ‰ Л˜ВТНУИ Л ФОУТНУИ ‚УОМ. кВБЫО¸Ъ‡Ъ ЩУНЫТЛ У‚НЛ Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ М‡НОУММЫ˛ Ф flПЫ˛ ОЛМЛ˛ ‚ ФОУТНУТЪЛ, Ф‡-‡ООВО¸МУИ БУММУИ ФО‡ТЪЛМНВ.

к‡ТТПУЪ ВММ˚В Ф ЛПВ ˚ ‰ВПУМТЪ Л Ы˛Ъ ‚УБПУКМУТЪ¸ ФУОЫ˜ВМЛfl БУММ˚ı ФО‡ТЪЛМУН Т ‡БОЛ˜- МУИ ЩУ ПУИ БУМ. З ЪУ КВ ‚ ВПfl Ф В‰ТЪ‡‚ОflВЪ ЛМЪВ-ВТ ФУТЪ УВМЛВ 2D ·ЛМ‡ М˚ı У· ‡БУ‚ БУМ о ВМВОfl ‰Оfl ·УОВВ ТОУКМ˚ı ТОЫ˜‡В‚, М‡Ф ЛПВ ‰Оfl БУММУИ ФО‡ТЪЛМ˚, ЩУНЫТЛ Ы˛˘ВИ ‚ Ф У‰УО¸М˚И ЛОЛ ФУФВ-В˜М˚И УЪ ВБУН Б‡‰‡ММУИ ‰ОЛМ˚ НУО¸ˆУ ЛОЛ Н‡НЫ˛- ОЛ·У ‰ Ы„Ы˛ „ВУПВЪ Л˜ВТНЫ˛ ЩЛ„Ы Ы. Сйщ Ъ‡НУ„УУ‰‡ ФУОЫ˜ЛОЛ М‡Б‚‡МЛВ ЩУНЫТ‡ЪУ У‚. к‡ТТПУЪ ЛП ‰Оfl Ф ЛПВ ‡ ЩУНЫТ‡ЪУ ‚ НУО¸ˆУ. лУУЪ‚ВЪТЪ‚Ы˛˘ЛИ У· ‡Б БУМ о ВМВОfl В¯ВЪНЛ ПУКВЪ ·˚Ъ¸ ФУОЫ˜ВМ ФЫЪВП НУП·ЛМ‡ˆЛЛ 1D ‰ЛЩ ‡НˆЛУММУИ В¯ВЪНЛ Л БУММУИ ФО‡ТЪЛМНЛ. ЗУБ¸ПВП ‰УТЪ‡ЪУ˜МУ ЫБНЛИ ТВ„- ПВМЪ 1D ‰ЛЩ ‡НˆЛУММУИ В¯ВЪНЛ, НУЪУ ˚И ‚В‰ВЪ ТВ·fl Ъ‡Н КВ, Н‡Н ˆВО‡fl ‰ЛЩ ‡НˆЛУММ‡fl В¯ВЪН‡, ЪУ ВТЪ¸ УЪНОУМflВЪ ‚ıУ‰МУИ ПУМУı УП‡ЪЛ˜ВТНЛИ ФЫ˜УН

М‡ УФ В‰ВОВММ˚И Ы„УО ‚ ФОУТНУТЪЛ ( ‡ТТП‡Ъ Л‚‡ВЪТfl ФВ ‚˚И ФУ fl‰УН ‰ЛЩ ‡НˆЛЛ).

З ‡˘‡fl ТВ„ПВМЪ ‚УН Ы„ ˆВМЪ ‡ ФУОЫ˜ЛП Сйщ, БУМ˚ о ВМВОfl НУЪУ У„У УЪУ· ‡К‡˛ЪТfl ТЛТЪВПУИ‡‚МУУЪТЪУfl˘Лı НУМˆВМЪ Л˜ВТНЛı ˜В МУ-·ВО˚ı НУОВˆ У‰ЛМ‡НУ‚УИ ¯Л ЛМ˚. з‡БУ‚ВП В„У ‰ЛЩ ‡НˆЛУММ˚П ‡НТЛНУМУП. зВЪ Ы‰МУ ТУУ· ‡БЛЪ¸, ˜ЪУ Ъ‡НУИ Сйщ ·Ы‰ВЪ УЪНОУМflЪ¸ ‚ıУ‰МУИ ФЫ˜УН М‡ УФ В‰ВОВМ- М˚И ЪВОВТМ˚И Ы„УО ‚ Ф УТЪ ‡МТЪ‚В. СОfl ЪУ„У ˜ЪУ·˚ ТУ· ‡Ъ¸ ‰ЛЩ ‡„Л У‚‡ММ˚В ФЫ˜НЛ ‚ ЩУН‡О¸МУИ ФОУТНУТЪЛ, Ф ЛПВМЛП БУММЫ˛ ФО‡ТЪЛМНЫ, Ф Л˜ВП ‰Л- Щ ‡НˆЛУММ˚И ‡НТЛНУМ Л БУММ‡fl ФО‡ТЪЛМН‡ ПУ„ЫЪ ·˚Ъ¸ ТУ‚ПВ˘ВМ˚ ‚ У‰МУИ ФОУТНУТЪЛ Л Б‡ФЛТ‡М˚ М‡ У‰МУИ ФУ‰ОУКНВ. и Л ˝ЪУП ‚ ФОУТНУТЪЛ Сйщ У· ‡БЫВЪТfl ТЛТЪВП‡ НУМˆВМЪ Л˜ВТНЛı, МВ ‡‚МУПВ МУ УЪТЪУ- fl˘Лı НУОВˆ ФВ ВПВММУИ ¯Л ЛМ˚. н‡НЛП У· ‡БУП, П˚ ТЛМЪВБЛ У‚‡ОЛ ‡ПФОЛЪЫ‰М˚И Сйщ, ЩУНЫТЛ Ы˛- ˘ЛИ ‚ НУО¸ˆУ.

лОВ‰Ыfl УФЛТ‡ММУИ ПВЪУ‰ЛНВ ПУКМУ ФУТЪ УЛЪ¸‡БОЛ˜М˚В ЩУНЫТЛ Ы˛˘ЛВ Сйщ. з‡Ф ЛПВ , Б‡ФЛ- Т˚‚‡fl М‡ У‰МУИ ФУ‰ОУКНВ ‰‚В ТН В˘ВММ˚В ˆЛОЛМ‰-Л˜ВТНЛВ ОЛМБ˚ Т ‡БМ˚ПЛ ЩУНЫТМ˚ПЛ ‡ТТЪУflМЛflПЛ ПУКМУ ФУОЫ˜ЛЪ¸ Сйщ, ЩУНЫТЛ Ы˛˘ЛИ ‚ УЪ ВБУН, ОВК‡˘ЛИ ‚ ФОУТНУТЪЛ, ФВ ФВМ‰ЛНЫОfl МУИ УТЛ ‡Т- Ф УТЪ ‡МВМЛfl ( ЛТ. 3).

иУ-‚Л‰ЛПУПЫ, МВЪ УТУ·УИ МВУ·ıУ‰ЛПУТЪЛ „У‚У-ЛЪ¸, ˜ЪУ Л ЩУНЫТ‡ЪУ ‚ НУО¸ˆУ, Л ЩУНЫТ‡ЪУ ‚ ФУФВ-В˜М˚И УЪ ВБУН ПУ„ЫЪ ·˚Ъ¸ В‡ОЛБУ‚‡М˚ Н‡Н Щ‡БУ- ‚˚В Сйщ. СУТЪЛ˜¸ ˝ЪУ„У ‚ Ф УТЪВИ¯ВП ТОЫ˜‡В ПУКМУ ФЫЪВП ЩУЪУ„ ‡ЩЛ˜ВТНУ„У УЪ·ВОЛ‚‡МЛfl ТУУЪ‚ВЪТЪ‚Ы- ˛˘Лı ‡ПФОЛЪЫ‰М˚ı П‡ТУН (ЩУЪУ¯‡·ОУМУ‚).

иУ ТЫ˘ВТЪ‚Ы ‚ ‰‚Ыı ЪУО¸НУ ˜ЪУ ‡ТТПУЪ ВММ˚ı Ф ЛПВ ‡ı В˜¸ Л‰ВЪ У Щ‡БУ‚УИ ПУ‰ЫОflˆЛЛ, Ф Л НУЪУ-УИ У‰М‡ ·ЛМ‡ М‡fl ЩЫМНˆЛfl, УФЛТ˚‚‡˛˘‡fl ‰ЛЩ ‡Н- ˆЛУММЫ˛ В¯ВЪНЫ, ЫПМУК‡ВЪТfl М‡ ‰ Ы„Ы˛. й‰М‡НУ Ф УˆВТТ ПУ‰ЫОflˆЛЛ Ф‡ ‡ПВЪ У‚ ‰ЛЩ ‡НˆЛУММУИ В- ¯ВЪНЛ ПУКВЪ УТЫ˘ВТЪ‚ОflЪ¸Тfl Л Ф Л ·УОВВ ¯Л УНУП НО‡ТТВ ПУ‰ЫОЛ Ы˛˘Лı ЩЫМНˆЛИ. З ˜‡ТЪМУТЪЛ, УТЫ- ˘ВТЪ‚Оflfl ПУ‰ЫОflˆЛ˛ ‡‰ЛЫТУ‚ НУОВˆ БУММУИ ФО‡Т- ЪЛМНЛ ПУКМУ ФУТЪ УЛЪ¸ ЩУНЫТ‡ЪУ ‚ ТУУТМ˚И УЪ В- БУН УФ В‰ВОВММУИ ‰ОЛМ˚, НУЪУ ˚И Щ‡НЪЛ˜ВТНЛ ·Ы‰ВЪ

îÓ͇θÌ˚È ÓÚ ÂÁÓÍ z

y

éÒ‚Â˘‡˛˘ËÈ

ÔÛ˜ÓÍ

x

êËÒ. 3. кВБЫО¸Ъ‡Ъ ЩУНЫТЛ У‚НЛ ‰‚ЫПfl ТН В˘ВМ- М˚ПЛ ˆЛОЛМ‰ Л˜ВТНЛПЛ ОЛМБ‡ПЛ

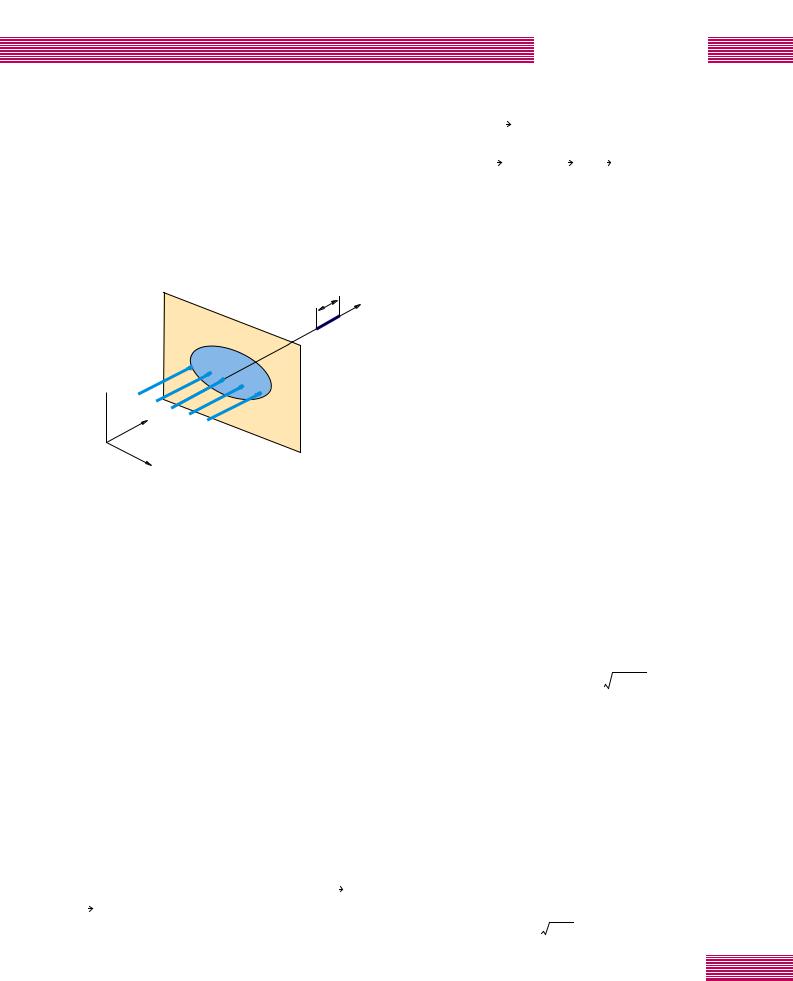
Ф В‰ТЪ‡‚ОflЪ¸ ТУ·УИ БУММЫ˛ ФО‡ТЪЛМНЫ Т Ф УЪflКВММУИ Ф У‰УО¸МУИ ‡·В ‡ˆЛВИ. а‰Вfl ФУОЫ˜ВМЛfl ТУУЪ‚ВЪТЪ‚Ы˛˘В„У ‡‰Л‡О¸МУ-ТЛППВЪ Л˜МУ„У Сйщ ТУТЪУЛЪ ‚ ЪУП, ˜ЪУ·˚ В„У ФВ ЛЩВ ЛИМ‡fl ˜‡ТЪ¸ ТУУЪ- ‚ВЪТЪ‚У‚‡О‡ БУММУИ ФО‡ТЪЛМНВ Т ЩУНЫТМ˚П ‡ТТЪУflМЛВП F1 , ‡ ˆВМЪ ‡О¸М‡fl ˜‡ТЪ¸ – БУММУИ ФО‡ТЪЛМНВ Т‡ТТЪУflМЛВП F2 > F1. еВК‰Ы ˆВМЪ ‡О¸МУИ Л ФВ ЛЩВ-ЛИМУИ ˜‡ТЪflПЛ ‰УОКМ˚ ·˚Ъ¸ Б‡ФЛТ‡М˚ НУО¸ˆ‡, ТУУЪ‚ВЪТЪ‚Ы˛˘ЛВ БУММ˚П ФО‡ТЪЛМН‡П, ЩУНЫТМУВ ‡Т- ТЪУflМЛВ НУЪУ ˚ı ЫПВМ¸¯‡ВЪТfl УЪ F2 Í F1. З ВБЫО¸Ъ‡ЪВ ·Ы‰ВЪ ФУОЫ˜ВМ ЩУНЫТ‡ЪУ ‚ ТУУТМ˚И УЪ ВБУН ‰ОЛМ˚ l = F2 − F1 . з‡ ЛТ. 4 ФУН‡Б‡М Ф УˆВТТ ЩУНЫТЛ У‚НЛ.

l

z

F2

F1

y

z

éÒ‚Â˘‡˛˘ËÈ

ÔÛ˜ÓÍ

x

êËÒ. 4. кВБЫО¸Ъ‡Ъ ЩУНЫТЛ У‚НЛ ‚ ТУУТМ˚И УЪ ВБУН

й·˘ЛВ ПВЪУ‰˚ ФУОЫ˜ВМЛfl ПУ‰ЫОЛ У‚‡ММ˚ı ‰Л- Щ ‡НˆЛУММ˚ı В¯ВЪУН, У·О‡‰‡˛˘Лı Б‡‰‡ММ˚ПЛ ЩЫМНˆЛУМ‡О¸М˚ПЛ Т‚УИТЪ‚‡ПЛ, Ъ В·Ы˛Ъ В¯ВМЛfl У· ‡ЪМ˚ı Б‡‰‡˜ ЪВУ ЛЛ ‰ЛЩ ‡НˆЛЛ. б‡ПВЪЛП, ˜ЪУВ¯ВМЛВ У· ‡ЪМУИ Б‡‰‡˜Л ‰ЛЩ ‡НˆЛЛ УТЫ˘ВТЪ‚ОflВЪТfl УЪМУТЛЪВО¸МУ Щ‡БУ‚УИ ЩЫМНˆЛЛ Сйщ, НУЪУ ˚И ‚˚ФУОМflВЪ Ъ В·ЫВПУВ Ф ВУ· ‡БУ‚‡МЛВ Т‚ВЪУ‚У„У ФЫ˜- Н‡. щЪ‡ Щ‡БУ‚‡fl ЩЫМНˆЛfl ‰УОКМ‡ ·˚Ъ¸ Б‡ФЛТ‡М‡ М‡ УФЪЛ˜ВТНЫ˛ Т В‰Ы ‚ ‚Л‰В БУМЛ У‚‡ММУИ ТЪ ЫНЪЫ ˚ Т Щ‡БУ‚˚П ПЛН У ВО¸ВЩУП, ‚ ВБЫО¸Ъ‡ЪВ ˜В„У Л ФУОЫ- ˜‡ВЪТfl Сйщ.

ЙкДзасх бйз а оДбйЗхЦ омздсаа СаокДдсайззхп йинауЦлдап щгЦеЦзнйЗ

è ˂‰ÂÌË ÙÛÌ͈ËË Í ËÌÚ ‚‡ÎÛ

èÓ‰ Ù‡ÁÓ‚ÓÈ ÙÛÌ͈ËÂÈ ϕ(u, υ) УФЪЛ˜ВТНУ„У ˝ОВПВМЪ‡ ·Ы‰ВП ФУМЛП‡Ъ¸ ЩЫМНˆЛ˛, УФЛТ˚‚‡˛˘Ы˛ Б‡- ‚ЛТЛПУТЪ¸ УЪ Ф УТЪ ‡МТЪ‚ВММ˚ı НУУ ‰ЛМ‡Ъ ‚ВОЛ˜Л- М˚ М‡·В„‡ Щ‡Б˚, ТУБ‰‡‚‡ВПУИ УФЪЛ˜ВТНЛП ˝ОВПВМЪУП ‚ ЪУ˜НВ (u, υ).

аМУ„‰‡ „ ‡МЛˆ˚ БУМ Сйщ ПУ„ЫЪ ·˚Ъ¸ ФУОЫ˜ВМ˚ ЛТıУ‰fl ЛБ Щ‡БУ‚˚ı ЩЫМНˆЛИ ТУУЪ‚ВЪТЪ‚Ы˛˘Лı Ъ ‡‰Л- ˆЛУММ˚ı ( ВЩ ‡НˆЛУММ˚ı) УФЪЛ˜ВТНЛı ˝ОВПВМЪУ‚.

н ‡‰ЛˆЛУММ˚И УФЪЛ˜ВТНЛИ ˝ОВПВМЪ ı‡ ‡НЪВ-ЛБЫВЪТfl „О‡‰НУИ Щ‡БУ‚УИ ЩЫМНˆЛВИ ϕ(u), „‰Â

u = (u, υ) – ФУФВ В˜М˚В НУУ ‰ЛМ‡Ъ˚ ЪУ˜НЛ, ОВК‡- ˘ВИ ‚ ФОУТНУТЪЛ УФЪЛ˜ВТНУ„У ˝ОВПВМЪ‡. и Л УТ‚В˘В-

МЛЛ УФЪЛ˜ВТНУ„У ˝ОВПВМЪ‡ ФЫ˜НУП Т НУПФОВНТМУИ

‡ПФОЛЪЫ‰УИ W0(u) МВФУТ В‰ТЪ‚ВММУ Б‡ УФЪЛ˜ВТНЛП ˝ОВПВМЪУП У· ‡БЫВЪТfl ФУОВ

W (u) = exp [iϕ(u)]W0(u). (6)

нУО˘ЛМ‡ Ъ ‡‰ЛˆЛУММУ„У УФЪЛ˜ВТНУ„У ˝ОВПВМЪ‡ H ПУКВЪ ТУТЪ‡‚ОflЪ¸ Ъ˚Тfl˜Л ‰ОЛМ ‚УОМ. и Л ˝ЪУП БМ‡˜ВМЛfl Щ‡Б˚ ϕ ОВК‡Ъ ‚ ЛМЪВ ‚‡ОВ УЪ 0 ‰У Ъ˚Тfl˜ В‰ЛМЛˆ 2π. З ЪУ КВ ‚ ВПfl ЛБПВМВМЛfl Щ‡Б˚ М‡ ‡Т- ТПУЪ ВММ˚ı ‡МВВ Сйщ ОВК‡Ъ ‚ ‰Л‡Ф‡БУМВ УЪ 0 ‰У 2π.

C Ы˜ВЪУП ЪУ„У, ˜ЪУ НУПФОВНТМ‡fl ˝НТФУМВМЪ‡ ‚ ‚˚ ‡КВМЛЛ (6) fl‚ОflВЪТfl ФВ ЛУ‰Л˜ВТНУИ ЩЫМНˆЛВИ Т ФВ ЛУ‰УП 2π, Щ‡Б‡ ПУКВЪ ·˚Ъ¸ Ф Л‚В‰ВМ‡ Н ЛМЪВ - ‚‡ОЫ [0, 2π). и Л‚В‰ВМЛВ Н ЛМЪВ ‚‡ОЫ ПУКМУ ‚˚ФУОМЛЪ¸ ФУ ЩУ ПЫОВ

аБ Ф ‡НЪЛ˜ВТНЛı ТУУ· ‡КВМЛИ ПУКВЪ УН‡Б‡Ъ¸Тfl ˆВОВТУУ· ‡БМ˚П Ф Л‚У‰ЛЪ¸ Щ‡БЫ Н ЛМЪВ ‚‡ОЫ [0, 2πm) ÔÓ ÙÓ ÏÛ·Ï

„‰Â Ó·˚˜ÌÓ m 1–102. щН‚Л‚‡ОВМЪМУТЪ¸ ЛТıУ‰МУИ „О‡‰НУИ Щ‡Б˚ ϕ Л Ф Л‚В‰ВММУИ Н ЛМЪВ ‚‡ОЫ НЫТУ˜- МУИ Щ‡Б˚ Φ ‚˚ ‡К‡ВЪТfl ТУУЪМУ¯ВМЛВП

иОУТН‡fl ТЩВ Л˜ВТН‡fl ОЛМБ‡

м ‡‚МВМЛВ Щ‡БУ‚УИ ЩЫМНˆЛЛ ТЩВ Л˜ВТНУИ ОЛМ- Б˚ ‚ Ф‡ ‡НТЛ‡О¸МУП Ф Л·ОЛКВМЛЛ ЛПВВЪ ‚Л‰

„‰Â k = 2π/λ – ‚ÓÎÌÓ‚Ó ˜ËÒÎÓ, f – ЩУНЫТМУВ ‡Т-

ÒÚÓflÌËÂ, D – ‰Ë‡ÏÂÚ ÎËÌÁ˚, r = u2 + υ2.

ЦТОЛ П‡ЪВ Л‡О ОЛМБ˚ ЛПВВЪ НУ˝ЩЩЛˆЛВМЪ Ф В- ОУПОВМЛfl n, ÚÓ Ï‡ÍÒËχθ̇fl ‚˚ÒÓÚ‡ ÂθÂÙ‡ ÒÓÒÚ‡‚ÎflÂÚ

λ

hmax = -----------

n –1

Л ЛПВВЪ ФУ fl‰УН ‰ОЛМ˚ ‚УОМ˚. З˚ТУЪ‡ ПЛН У ВО¸В- Щ‡ УФ В‰ВОflВЪТfl ФУ ЩУ ПЫОВ

к‡БОЛ˜М˚П Ы„О‡П УЪНОУМВМЛfl β ТУУЪ‚ВЪТЪ‚Ы˛Ъ‡БОЛ˜М˚В ФВ ЛУ‰˚ В¯ВЪНЛ

λ

d = ----------, sinβ

„‰Â sinβ = (n − 1)tgα.

ÅË̇ ̇fl 1D ‡ПФОЛЪЫ‰М‡fl ‰ЛЩ ‡НˆЛУММ‡fl В- ¯ВЪН‡ ФУОЫ˜‡ВЪТfl Ф Л Б‡ПВМВ ОЛМВИМУ ПВМfl˛˘ВИТfl Щ‡БУ‚УИ ЩЫМНˆЛЛ ‚ Ф В‰ВО‡ı У‰МУ„У ФВ ЛУ‰‡ М‡

‰‚Ó˘ÌÛ˛ ÙÛÌÍˆË˛, Ô ËÌËχ˛˘Û˛ Á̇˜ÂÌËfl ±π/2.

дУП·ЛМЛ У‚‡ММ˚В Л ТВ„ПВМЪЛ У‚‡ММ˚В Сйщ

З˚¯В ЫКВ „У‚У ЛОУТ¸ У ‚УБПУКМУТЪЛ ФУОЫ˜ВМЛfl НУП·ЛМЛ У‚‡ММ˚ı БУММ˚ı ФО‡ТЪЛМУН, Ф В‰ТЪ‡‚Оfl- ˛˘Лı ТУ·УИ ТЫФВ ФУБЛˆЛ˛ ‰‚Ыı ЛТıУ‰М˚ı БУММ˚ı ФО‡ТЪЛМУН.

ЦТОЛ ‰‚‡ ‡ТФУОУКВММ˚ı ТУУТМУ ‰ Ы„ Б‡ ‰ Ы„УП УФЪЛ˜ВТНЛı ˝ОВПВМЪ‡ ЛПВ˛Ъ Щ‡БУ‚˚В ЩЫМНˆЛЛ ϕ1 Ë ϕ2 ТУУЪ‚ВЪТЪ‚ВММУ, ЪУ УМЛ ПУ„ЫЪ ·˚Ъ¸ Б‡ПВМВМ˚ НУП- ·ЛМЛ У‚‡ММ˚П УФЪЛ˜ВТНЛП ˝ОВПВМЪУП Ò Ù‡ÁÓ‚ÓÈ ÙÛÌ͈ËÂÈ ϕ = ϕ1 + ϕ2 .

êËÒ. 6. СЛЩ ‡НˆЛУММ‡fl В¯ВЪН‡ Т ·ОВТНУП

иОУТНУТЪ¸ ТВ„ПВМЪЛ У‚‡ММУ„У Сйщ ‚ Ф В‰ВО‡ı ‡ФВ ЪЫ ˚ ‡Б·Л‚‡ВЪТfl М‡ ‰‚‡ ЛОЛ ·УО¸¯ВВ ˜ЛТОУ ТВ„- ПВМЪУ‚, ‡ ‚ Н‡К‰УП ЛБ ТВ„ПВМЪУ‚ Б‡ФЛТ˚‚‡ВЪТfl БУМ- М‡fl ФО‡ТЪЛМН‡, ТУУЪ‚ВЪТЪ‚Ы˛˘‡fl УФ В‰ВОВММУИ Щ‡- БУ‚УИ ЩЫМНˆЛЛ. з‡Ф ЛПВ , Ъ‡НЛП У· ‡БУП ПУКМУ ФУОЫ˜ЛЪ¸ ЩУНЫТ‡ЪУ ‚ ·ЫН‚Ы R, ЩУЪУ¯‡·ОУМ НУЪУ У- „У Ф Л‚В‰ВМ М‡ ЛТ. 7.

ганЦкДнмкД

1. ÅÓ Ì å., ÇÓθ٠ù. йТМУ‚˚ УФЪЛНЛ. е.: з‡ЫН‡, 1973. 720 Т.

* * *

ЗЛНЪУ АОВНТ‡М‰ У‚Л˜ лУИЩВ , Ф УЩВТТУ ,ВНЪУ л‡П‡ ТНУ„У „УТЫ‰‡ ТЪ‚ВММУ„У ‡˝ УНУТПЛ- ˜ВТНУ„У ЫМЛ‚В ТЛЪВЪ‡, ТФВˆЛ‡ОЛТЪ ‚ У·О‡ТЪЛ У· ‡- ·УЪНЛ ЛБУ· ‡КВМЛИ Л НУПФ¸˛ЪВ МУИ УФЪЛНЛ. г‡Ы-В‡Ъ ЙУТЫ‰‡ ТЪ‚ВММУИ Ф ВПЛЛ кУТТЛЛ ‚ У·О‡ТЪЛ М‡ЫНЛ Л ЪВıМЛНЛ 1992 „У‰‡ Б‡ ‡Б ‡·УЪНЫ О‡БВ М˚ı ЪВıМУОУ„ЛИ Л Лı ‚МВ‰ ВМЛВ Ф Л ТУБ‰‡МЛЛ МУ‚УИ ‡‚Л‡ˆЛУММУ-НУТПЛ˜ВТНУИ ЪВıМЛНЛ. уОВМ ПВК‰ЫМ‡-У‰МУ„У УФЪЛ˜ВТНУ„У У·˘ВТЪ‚‡ SPIE. А‚ЪУ 310 М‡- Ы˜М˚ı ‡·УЪ, ‚ ЪУП ˜ЛТОВ Ъ Вı ПУМУ„ ‡ЩЛИ, 50 ‡- ·УЪ ‚ Б‡ Ы·ВКМ˚ı ЛБ‰‡МЛflı.